
Учебник 2
.pdf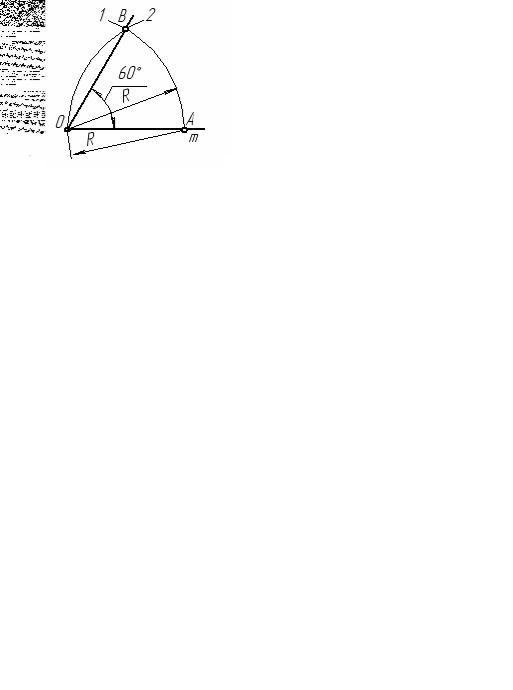
точки А на той же прямой тем же радиусом проводится дуга 2 до пересечения с дугой 1 в точке В. Угол АОВ – искомый.
Для деления угла пополам из вершины заданного угла нужно провести дугу произвольного радиуса R до пересечения со сторонами угла в точках А и В (рис. 2.8).
|
|
Рис. 2.7 |
Рис. 2.8 |
Из полученных точек, как из центров, проводятся две дуги равных радиусов до их взаимного пересечения в точке М. Биссектриса ОМ поделит заданный угол пополам.
2.2. Деление окружности на равные части. Построение правильных многоугольников
Чтобы разделить окружность на равные части, прежде всего нужно определить центр дуги (рис. 2.9). Для этого на дуге окружности намечают три произвольно расположенные точки А, В и С. Эти точки соединяют прямыми АВ и ВС для получения хорд данной дуги. Точка пересечения перпендикуляров, проведенных через середины хорд (см. построение на рис. 2.1), показывает положение центра исходной дуги.
|
|
|
|
|
|
Рис. 2.9 |
|
Рис. 2.10 |
Для определения центра окружности в заданной окружности
необходимо провести две не параллельные между собой хорды АВ и СD

(рис. 2.10). Через середины хорд проводят перпендикуляры (см. построение на рис. 2.1), пересечение которых и определит положение центра исходной окружности.
Разделим окружность на три, шесть и двенадцать частей (рис. 2.11). В окружности заданного радиуса R проведем через центр О взаимно перпендикулярные оси АВ и CD. Из любой точки конца диаметра (например, А) проведем дугу радиусом R до пересечения с окружностью в точках 1 и 2. Отрезок 1–2 – это искомая сторона правильного вписанного треугольника 1В2. В свою очередь отрезки А1 = А2 и С1 = D2 равны сторонам правильных вписанных шестиугольника и двенадцатиугольника соответственно. Для построения недостающих точек (вершин углов) достаточно провести из точки В противоположного конца диаметра окружности дугу того же радиуса R до пересечения с окружностью или последовательно отложить измерителем соответствующие отрезки на основной окружности.
Чтобы разделить окружность на четыре и восемь частей, необходимо провести два взаимно перпендикулярных диаметра АВ и CD (рис. 2.12). Отрезки АС = СВ = BD, соединяющие концы диаметров, являются искомыми сторонами правильного четырехугольника, вписанного в окружность.
Для деления окружности на восемь частей из центра О строят перпендикуляр к одной из сторон (например, АС) и продолжают его до пересечения с окружностью в точке М. Отрезок АМ – это искомая сторона правильного восьмиугольника, вписанного в окружность.
|
|
|
|
Рис. 2.11 |
Рис. 2.12 |
|
Рис. 2.13 |
Для деления окружности на пять и десять частей проводят два взаимно перпендикулярных диаметра АВ и CD и делят радиус ОВ пополам в точке М (рис. 2.13). Из точки М, как из центра, проводят дугу радиусом МC до пересечения ее с диаметром АВ в точке K. Отрезок СK равен стороне правильного вписанного пятиугольника, отрезок ОK – десятиугольника. Для деления окружности на пять
частей достаточно дугой радиуса СK сделать засечки на исходной окружности в точках 1, 2 и далее; используя точки 1 и 2 как центры, тем же радиусом отметить точки 3 и 4. Точки С, 1, 3, 4, 2 – это вершины правильного вписанного пятиугольника.
2.3. Построение уклона и конусности
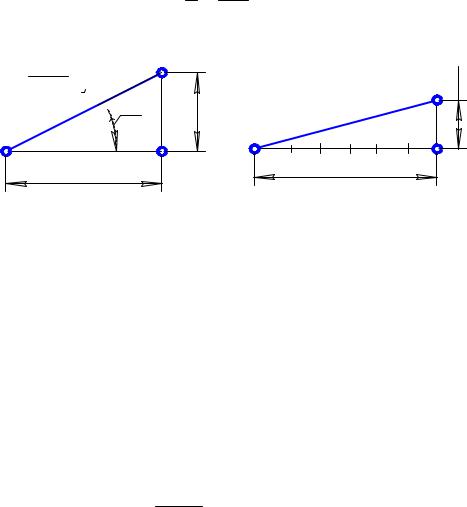
Уклон – это величина, которая характеризует наклон одной линии по отношению к другой (рис. 2.14). Уклон i прямой АС относительно прямой АВ (рис. 2.14, а) определяется как отношение разности высот двух точек А и С к горизонтальному расстоянию между ними:
×1:3

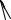 a
a
A l
а
i = h = BC = tg α. l AB
C
|
C |
h |
|
|
A |
B |
6 частей |
|
б |
|
Рис. 2.14 |
1 часть
B
Покажем, как провести через точку А прямую заданного уклона 1 : 6 (рис. 2.14, б). Из точки А построим горизонтальный луч и отметим на нем шесть произвольных равных отрезков. На перпендикуляре, восставленном из конечной точки В, отложим одну такую часть. Уклон гипотенузы АС треугольника АСВ будет равен 1 : 6.
Конусность K определяется как отношение разности диаметров D и d двух поперечных сечений конуса к расстоянию l между ними
(рис. 2.15):
K = D l−d = 2tg α, K = 2i.
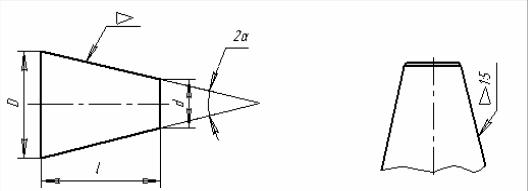
Рис. 2.15
Перед размерным числом конусности ставится знак конусности  – равнобедренный треугольник, вершина которого направлена в сторону вершины конуса.
– равнобедренный треугольник, вершина которого направлена в сторону вершины конуса.
Значения конусности и углы конусов, рекомендованные ГОСТ 8583–81, приведены в табл. 2.1.
Таблица 2.1
Нормальные конусности и углы конусов по ГОСТ 8593–81 ( СТ СЭВ 512–77)
Конусность |
|
Угол конуса α |
||
|
|
в угловых единицах |
рад |
|
1: 500 |
0,002 000 0 |
6' 52,5'' |
0,002 000 0 |
|
1: 200 |
0,005 000 0 |
17' 11,3'' |
0,005 000 0 |
|
1: 100 |
0,010 000 0 |
34' 22,6'' |
0,010 000 0 |
|
1: 50 |
0,020 000 0 |
1º 8' 45,2'' |
0,019 999 6 |
|
1: 30 |
0,033 333 3 |
1º 54' |
34,9'' |
0,033 330 4 |
1: 20 |
0,050 000 0 |
2º 51' |
51,1'' |
0,049 989 6 |
1: 15 |
0,066 666 7 |
3º 49' 5,9'' |
0,066 642 0 |
|
1: 12 |
0,083 333 3 |
4º 46' |
18,8'' |
0,083 285 2 |
1: 10 |
0,100 000 0 |
5º 43' |
29,3'' |
0,099 916 8 |
1: 8 |
0,125 000 0 |
7º 9' |
9,6'' |
0,124 837 6 |
1: 7 |
0,142 857 1 |
8º 10' |
16,4'' |
0,142 614 8 |
1: 6 |
0,166 666 7 |
9º 31' |
38,2'' |
0,166 282 4 |
1: 5 |
0,200 000 0 |
11º25' 16,3'' |
0,199 337 4 |
|
1: 4 |
0,250 000 0 |
14º15' 0,1'' |
0,248 710 0 |
|
1: 3 |
0,333 333 3 |
18º 55' 28,7'' |
0,330 297 2 |
|
1: 1,866 025 |
0,535 898 5 |
30º |
0,523 598 8 |
|
1: 1,207 107 |
0,828 426 9 |
45º |
0,786 398 2 |
|
1: 0,866 025 |
1,154 701 0 |
60º |
1,047 197 6 |
|
1: 0,651 613 |
1,534 653 2 |
75º |
1,308 997 0 |
|
1: 0,500 000 |
2,000 000 0 |
90º |
1,570 796 4 |
|
1: 0,288 675 |
3,464 103 2 |
120º |
2,094 395 2 |
|
2.4. Сопряжения
Сопряжением принято называть плавный переход одной линии в
другую, прямой линии в дугу или одной дуги в другую. Общая для этих линий точка называется точкой сопряжения, или точкой перехода.
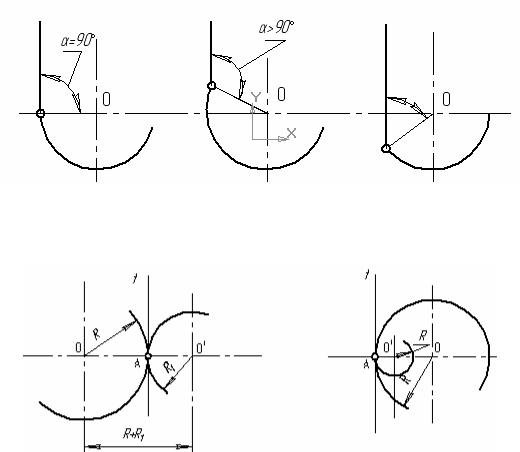
Плавный переход прямой линии в дугу обеспечивается лишь тогда, когда прямая является касательной к дуге, т. е. когда точка сопряжения лежит на перпендикуляре, опущенном на прямую из центра окружности, которой принадлежит дуга (рис. 2.16, а). Если это условие
не выполняется, то переход будет не плавным, а с изгибом (рис. 2.16, б,
в).
Плавный переход одной окружности в другую достигается тогда, когда окружности имеют общую касательную t в точке сопряжения А, лежащей на прямой, соединяющей центры окружностей, которым принадлежат дуги (рис. 2.17). Касание называется внешним,
если центры О и О1 лежат по разные стороны от касательной t (рис. 2.17, а), и внутренним, если центры находятся по одну сторону от
общей касательной (рис. 2.17, б).
а |
б |
в |
Рис. 2.16
а |
б |
Рис. 2.17

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов, а при внутреннем – разности их радиусов.
В общем случае построение сопряжения двух линий при заданном радиусе сопряжения состоит из следующих этапов:
–построения множества точек, находящихся на расстоянии радиуса сопряжения от первой из сопрягаемых линий;
–построения множества точек, находящихся на расстоянии радиуса сопряжения от второй из сопрягаемых линий;
–определения на пересечения множеств точек центра дуги сопряжения;
–определения точки сопряжения на первой из сопрягаемых линий;
–определения точки сопряжения на второй из сопрягаемых линий;
–проведения дуги сопряжения на интервале между точками сопряжения.
Далее рассмотрим сопряжение двух прямых линий дугой окружности, сопряжение прямой с окружностью, сопряжение двух заданных окружностей, а также построение овалов.
2.4.1. Сопряжение двух прямых линий дугой окружности
Для сопряжения сторон a и b прямого угла дугой радиуса R из вершины прямого угла, как из центра, проводят дугу окружности радиусом R до пересечения со сторонами a и b
прямого угла в точках А и В (рис. 2.18). Из этих точек, как из центров, тем же радиусом проводят дуги окружностей до их взаимного пересечения в точке О. Затем из этой точки О радиусом R проводят дугу сопряжения между точками А и В сопряжения.
Чтобы построить сопряжение сторон a и b острого угла дугой радиуса R, сначала
определяют центр дуги сопряжения, для чего на расстоянии R от сторон
a и b острого угла проводят прямые, параллельные этим сторонам, до их пересечения в точке О (рис. 2.19). Из центра О опускают перпендикуляры на заданные прямые, получают точки А и В сопряжения. Из точки О, как из центра, проводят дугу сопряжения радиусом R. Такое сопряжение часто применяют в различных деталях.

Элементы сопряжения сторон a и b тупого угла дугой радиуса R могут быть найдены так же, как и в предыдущем случае (рис. 2.20).
|
|
|
|
|
|
Рис. 2.19 |
Рис. 2.20 |
Для сопряжения двух параллельных прямых a и b дугой радиуса R проводят прямую с, перпендикулярную к прямым a и b, и получают точки А и В сопряжения, делят отрезок АВ пополам и из точки О, как из центра, проводят дугу сопряжения радиусом R = ОА (рис. 2.21).
Сопряжение двух пересекающихся прямых a и b, на одной из которых задана точка А сопряжения, выполняется следующим образом (рис. 2.22). Для определения центра О дуги сопряжения проводят биссектрису угла АВС между заданными прямыми до пересечения с перпендикуляром к прямой a, восставленным в точке А. Из точки О опускают перпендикуляр на прямую b и определяют точку В сопряжения. Радиусом ОА проводят дугу сопряжения.
При сопряжении двух параллельных прямых a и b, на одной из которых задана точка А сопряжения и расстояние между которыми равно h, для нахождения центра дуги сопряжения посередине между этими прямыми проводят параллельную им линию, которая будет множеством центров дуг сопряжения прямых (рис. 2.23). Восставив из точки А перпендикуляр к прямой а, находят точку О – центр дуги сопряжения – и точку В сопряжения. Через эти точки проводят дугу сопряжения радиусом R = h / 2.
ac À
1 R
|
O |
R |
R |
|
|
1 |
9 |
|
|
|
0 |
|
Å |
|
B |
C

a A


 O
O 
 R
R 



B



b
|
A |
a |
|
|
2/h |
R |
O |
h |
|
||
|
B |
b |
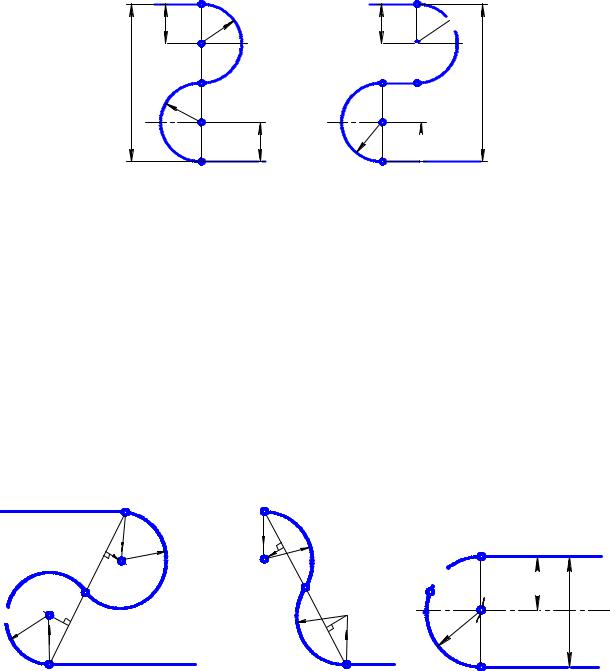
Рис. 2.21 |
Рис. 2.22 |
Рис. 2.23 |
Сопряжение двух параллельных прямых a и b в пределах ограниченной длины этих прямых выполняют аналогично показанному на рис. 2.24.
a |
|
A |
|
a |
h/4 |
|
R |
h/4 |
|
|
|
|
||
|
O 1 |
|
|
D |
h |
C |
|
|
|
|
|
|
||
|
|
|
|
|
|
R |
O |
2 |
|
|
|
|
||
|
|
|
h/4 |
R |
|
|
|
|
|
|
|
B |
b |
B |
|
а |
|
|
|
A
R 


O 1


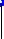


C
O 2
h/4
б
h
b
Рис. 2.24
Более сложным является сопряжение двух параллельных прямых а и b, если заданы точка А сопряжения и точка С касания дуг сопряжения (рис. 2.25). Соединив точки А и С, находят точку В сопряжения. Из середины отрезка АС восставляют перпендикуляр до пересечения с перпендикуляром, восставленным к прямой a в точке А. При пересечении перпендикуляров получают центр О1 первой дуги сопряжения. Аналогично находят центр О2 второй дуги сопряжения. Радиусами R1 = AО1 и R2 = BО1 проводят дуги сопряжения. Конфигурация сопряжения и радиусы R1 и R2 зависят от взаимного расположения точек А и С (рис. 2.25, а, б).
a
 R2
R2
A |
a |
A |
|
|
R |
1 |
R |
1 |
|
|
O 1 |
|||
|
|
|
|
||
|
O |
1 |
|
C |
|
|
|
|
|
||
O 2 |
|
|
|
|
|
C |
|
|
|
|
R2
O 2
B
A 




O
R
2/h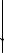
a
h
B |
b |
B |
b |
C |
b |
|
a |
б |
|
|
|
|
Рис. 2.25 |
|
|
|
Рис. 2.26 |
Еще один возможный случай сопряжения – это сопряжение двух параллельных прямых a и b, если задана точка А, через которую должна пройти дуга сопряжения (рис. 2.26). Для получения центра О дуги сопряжения проводят прямую, параллельную заданным прямым, посередине между этими прямыми. На пересечении полученной прямой с дугой, проведенной из заданной точки А, как из центра, радиусом, равным h/2, находят центр О дуги сопряжения. Через эту точку проводят перпендикуляр к прямым a и b и получают точки В и С сопряжения. Радиусом R = h / 2 проводят дугу сопряжения.
2.4.2. Сопряжение прямой с окружностью
Возможны три случая построения сопряжений прямой с окружностью: когда задан радиус дуги сопряжения; задана точка сопряжения на прямой; задана точка сопряжения на окружности.
Вкаждом из трех случаев сопряжение может быть внешним или внутренним.
Впервом случае прямая а сопрягается с окружностью радиу-
са R1 при заданном радиусе дуги сопряжения R (рис. 2.7, a, б). Из центра О1 (рис. 2.27, а) проводят вспомогательную дугу радиусом R1
+R до пересечения с прямой линией, проведенной параллельно прямой а на расстоянии R от нее и получают точку О – центр дуги сопряжения. Соединяя центры О1 и О прямой, в пересечении ее с заданной окружностью находят точку А сопряжения. Опустив перпендикуляр из точки О на прямую а, получают точку В сопряжения. Из точки О проводят дугу сопряжения радиусом R. В
рассматриваемом случае имеет место внешнее сопряжение, так как
ОО1 = R1 + R.
а |
б |
Рис. 2.27

Для построения внутреннего сопряжения, когда ОО1 = R1 – R, проводят вспомогательную дугу из центра О1 окружности радиусом R1 – R до пересечения ее с прямой, проведенной параллельно прямой а на расстоянии R от нее (рис. 2.27, б). Полученную точку О – центр дуги сопряжения – соединяют прямой с центром О1 заданной окружности. В пересечении этой прямой с окружностью получают точку А сопряжения. Опустив перпендикуляр из центра дуги сопряжения О на прямую а, находят точку В сопряжения. Из точки О проводят дугу сопряжения радиусом R.
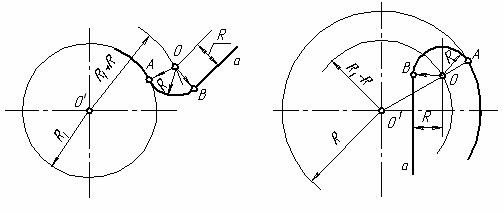
Второй случай – сопряжение прямой а с окружностью радиуса R1, если на прямой а задана точка А сопряжения (рис. 2.28). Из точки А (рис. 2.28, а) восставляют перпендикуляр к прямой а. На этом перпендикуляре будет находиться центр дуги сопряжения – точка О. На перпендикуляре откладывают отрезок АС = R1 и соединяют центр О1 заданной окружности с точкой С. Из середины отрезка СО1 восставливают перпендикуляр до пересечения с продолжением перпендикуляра СА в точке О – центре дуги сопряжения. Точки О и О1 соединяют прямой и в пересечении ее с заданной окружностью получают точку В сопряжения. Из этой точки проводят дугу сопряжения радиусом
R = ОB.
Построение внутреннего сопряжения (рис. 2.28, б), когда ОО1 = = R1 – R, аналогично описанному выше построению внешнего сопряжения.
а |
б |
Рис. 2.28
