Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

zajcevVM

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

1.25 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>

3) lim	sin( x − 3 )		4) lim (tg2 x + 1)	8−x
		;		x .
	x2 −8 x + 15
x→3			x→0

3.4. Исследовать функции y = f(x) на непрерывность. Найти точки разрыва, если они существуют, определить их тип. Построить схематический график функции.

1. 1)

2. 1)

3. 1)

4. 1)

5. 1)

6. 1)

7. 1)

y = e 2−x ;

y = arctg

;

x −1

y =

2 x −1

;

x2 + 5 x +

y =

x2 −1

;

x +

y =

;

3x −1

y =

1 − x

;

1 + x

y =

x3 −1

;

x −1

	− x,		если			x ≤ 0
2)			если			0 < x ≤π .
	y = sin x,
				если		x >π
	x + 1,
	x + 1,			если		x ≤ −1
2)				если		−1 < x ≤ 1 .
	y = x2 + 1,
	−x + 3,			если		x > 1

		1− x,			если		x ≤ 0
2)							0 < x < 2 .
	y = −( x −1 )2 , если
		x − 3,			если		x ≥ 2

	cos x,			если		x ≤ 0
2)				если		0 < x < 1 .
	y = x2 −1,
		1 − x,		если		x ≥ 1

		− x,		если		x ≤ 0
2)		− x2 ,		если		0 < x ≤ 2 .
	y = 1
	x −5,			если		x > 2

	x + 4,			если		x < −1
2)				если		−1 ≤ x < 0 .
	y = x2 + 2,
		e x ,		если		x ≥ 0

	−( x + 1 ),				если		x < −1
2)					если		−1 < x ≤ 0 .
	y = ( x + 1 )2 ,
		tgx ,			если x > 0

8. 1) y = ln x +x 2 ;

9. 1) y =	1	;
	1 + 21 / x

x −1

10. 1) y = x −1 x + 2 ;

11.1) y = 4 1+x ;

12.1) y = arcctg x x− 3 ;

13. 1)	y =	1 − 2 x				;
		(x − 2)2

14. 1)	y =	x2 − 4				;
		x	x −	2


15. 1)	y =	4 − x			;

		4 x −1

		− x2 ,				если	x ≤ 0
2)		tgx ,			если		0 < x ≤π / 4 .
	y =
		−1,			если		x >π / 4

		− 2 x ,				если		x ≤ 0
2)		x2 + 1,				если		0 < x ≤ 1 .
	y =
	2	+ ln x,				если		x > 1

		ex ,			если		x ≤ 0
2)			x,		если		0 < x < 4 .
	y =
		2 , если x ≥ 4


		x3 ,			если		x ≤ 0
2)					если		0 < x <π .
	y = cos x,
			1 ,		если		x ≥π

	1	− x2 ,				если x ≤ 0
2)		2	x	,		если	0 < x < 1 .
	y =
						если x ≥ 1
	2 x + 1,

	1 − x2 ,					если x ≤ 1
2)					если		1 < x < e .
	y = ln x,
	x + 1,				если x ≥ e

	3,					если x ≤ 0
2)		+ sin x, если						0 < x <π .
	y = 3
						если x ≥π
	x + 1,
	0,					если x ≤ 0
2)						если		0 < x < 0,5π .
	y = tgx,

	0,5π − x, если x ≥ 0,5π

16.1)

17.1)

18.1)

19.1)

20.1)

21.1)

22.1)

23.1)

y = 21 −− xx − xx ;

2 x

y = ( 2 )x+1 ;

y = lg x x+ 1 ;

y = x + 12 ; 2 + 3 x

y = 1x − 2 x−1 ;

x+1

y = ( 0,5 )x+2 ;

y = arctg1 x ; y = lg1x ;

	1	− x2 ,		если x ≤ −1
2)
2)	y = arctgx, если − 1 < x < 0 .
	5 x + 1, если x ≥ 0

					2	,	если x ≤ −π
	−(x / π )					,	если x ≤ −π
2)			если				−π < x < 0 .
2)	y = cos x,		если				−π < x < 0 .
			если x ≥ 0
	sin x,		если x ≥ 0

	arctgx,			если x ≤ 0
2)		− x2 ,		если 0 < x < 2 .
2)	y = 1	− x2 ,		если 0 < x < 2 .
	x −5,			если x ≥ 2

		e−x ,			если			x ≤ 0
2)		1 + x ,			если			0 < x < 3 .
2)	y =	1 + x ,			если			0 < x < 3 .
		1,			если			x ≥ 3
		1,			если			x ≥ 3

	1 + x,					если		x < −1
2)								−1 ≤ x ≤ 0 .
2)	y = ( x + 1 )2 , если							−1 ≤ x ≤ 0 .
		ctgx,			если			x > 0

		− x,			если x ≤ 1
	2	− x,			если x ≤ 1
2)	y = 1 + ln x, если							1 < x < e .
		x2 ,		если x ≥ e
		x2 ,		если x ≥ e
	x3 + 2,					если x ≤ 0
2)		+ cos x, если						0 < x <π .
2)	y = 1	+ cos x, если						0 < x <π .
	x −π,				если x ≥π

		10 x ,			если			x ≤ 0
2)		1 − x,			если			0 < x < 1 .
2)	y =	1 − x,			если			0 < x < 1 .
		x2 ,			если			x ≥ 1
		x2 ,			если			x ≥ 1

24.1)

25.1)

26.1)

27.1)

28.1)

29.1)

30.1)

y = 2 xx −+ 2x2 ;

y = 5 x x−5 ;

y = xx ++ 11 x2 −1 ;


y = arctg			x			;
y = arctg			x + 2			;
y =		x −1		;
y =	x2 −5 x			;
	x2 −5 x
y =		1 − x			;
y =		+ 31 / x			;
1		+ 31 / x
		2+x

y = 5 1−x ;

	1 − x2 , если x ≤ 0
					1
					1
2)		2 x ,					если 0 < x < 1 .
2)	y =	2 x ,					если 0 < x < 1 .
	x + 1,						если x ≥ 1



	arctgx, если x ≤ 0
2)							если	0 < x < 0,25π .
2)	y = tgx,						если	0 < x < 0,25π .
			− x,				если x ≥ 0,25π
	π		− x,				если x ≥ 0,25π
	cos x,						если	x ≤ 0

	1
2)	y =		,				если	0 < x < 1 .
2)	y =		,				если	0 < x < 1 .
	x	− x,						x ≥ 1
	2	− x,					если	x ≥ 1

	x + 1,						если		x ≤ −1
2)		2 −1,					если		−1 < x ≤ 0 .
2)	y = x	2 −1,					если		−1 < x ≤ 0 .
				x		+ 2, если			x > 0
	−e					+ 2, если			x > 0
	x − 2,						если x ≤ 0
2)
2)	y = −( x −1 )2 , если 0 < x < 1 .
				− ln x, если x ≥ 1

				− 2 x , если					x ≤ 0
2)									0 < x ≤ 1 .
2)	y = x2 + 1, если								0 < x ≤ 1 .
					x ,		если		x > 1
	2				x ,		если		x > 1
				x3 ,			если		x ≤ 0
2)		−ex ,					если	0 < x < 1 .
2)	y = 1	−ex ,					если	0 < x < 1 .
							если		x ≥ 1
	x + 1,						если		x ≥ 1

Раздел 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Литература: [ 2, модуль 9 ]; [ 3, глава 5 ]; [ 4, глава 3 ]; [ 5, глава 5 ].

1. Определение производной

Пусть функция y = f ( x ) определена в некоторой окрестности точки x. Да-

дим аргументу x приращение ∆x (при этом предполагается, что точка x + ∆x принадлежит области определения функции). Тогда функция получит приращение

∆y = f ( x + ∆x ) − f ( x ) .

Производной функции f ( x ) в точке x называется предел отношения прира-

щения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.

		Производная функции y = f ( x ) в точке x обозначается символами:								y′,
	′		dy		df ( x )

f		( x ) или dx		,	dx		. Итак, по определению
f		( x ) или dx		,	dx		. Итак, по определению
						f ′( x ) = lim		f ( x + ∆x ) − f ( x )	.	(4.1)
						f ′( x ) = lim			.	(4.1)
							∆x→0	∆x

Нахождение производной функции называется дифференцированием этой функции, функцию при этом называют дифференцируемой.

Справедлива теорема: если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.

Отсюда следует, что в точке разрыва функция не дифференцируема. Обратная теорема неверна: функция может быть непрерывной, но не иметь

производной.

Пример 4.1. Исходя из определения производной, найти производные функций: 1) f (x) = c, c – постоянная величина; 2) y = x .

Решение. 1) Запишем приращение функции ∆y = f ( x + ∆x ) − f ( x ) = c −c =0 .

Тогда	y′ =	lim	∆y	= 0 . Следовательно, (c)′ = 0 , т. е. производная постоян-
		∆x→0	∆x
ной величины равна нулю.
2) Функция		y =	x	определена при 0 ≤ x < +∞ . Составим приращение функ-
ции ∆y =	x + ∆x − x . Вычислим:
				85

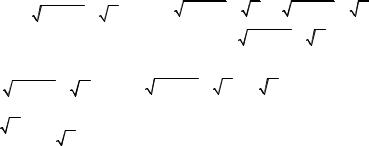
lim

∆y

lim

x + ∆x − x

= lim

(

x + ∆x − x ) ( x + ∆x + x )

∆x ( x + ∆x +

x )

∆x

∆x→0

= lim

x + ∆x − x

= lim

(

x )

∆x→0 ∆x

x + ∆x +

∆x→0

+ ∆x +

x 2 x

Итак,

y′ = (

x )′ =

Пример 4.2. Показать, что функция

f ( x ) =

непрерывна, но не дифферен-

цируема при x = 0 .

f (0) = 0,

(−x)

Решение.

Так

как

lim

= lim

= 0, lim

= lim x = 0 ,

x→0−0

x→0+0

x→0−0

то непрерывность функции показана.

Рассмотрим приращение функции при x = 0 :

∆ f = f ( 0 + ∆x ) − f ( 0 ) = f ( ∆x ) =

∆x

Если ∆x > 0 , то∆ f = ∆x и

lim

∆ f

= 1 .

∆x→0+0

∆x

∆ f

Если же ∆x < 0 , то ∆ f = −∆x и

lim

= −1 .

∆ f

∆x→0−0 ∆x

Следовательно,

lim

не существует, поэтому при x = 0 эта функция не

∆x→0

∆x

имеет производной.

Геометрический смысл производной: производная функции

y = f ( x ) в точке

x0 равна угловому коэффициенту

k = tgα касательной в точке

M0 ( x0 , f ( x0 ))

графика функции.

На этом основании получаем, что уравнение невертикальной касательной к

кривой y = f ( x ) в её точке M0 ( x0 , f ( x0 )) можно записать в виде
y − f ( x0 ) = f ′( x0 )( x − x0 ) .	(4.2)

Нормалью к кривой в её точке M0 называется прямая, проходящая через эту точку перпендикулярно касательной к кривой в этой точке.

Так как у двух взаимно перпендикулярных прямых угловые коэффициенты обратно пропорциональны и отличаются знаком, то уравнение нормали к кривой y = f ( x ) в точке M0 ( x0 , f ( x0 )) имеет вид

y − f ( x ) = −	1	( x − x	0	) ,	(4.3)
y − f ( x ) = −		( x − x		) ,	(4.3)
0	f ′( x0 )
если f ′( x0 ) ≠ 0 .	f ′( x0 )
если f ′( x0 ) ≠ 0 .
Механический смысл производной:	скорость прямолинейного				движения
v = v (t ) есть производная от пройденного пути s = s (t )				по времени t.

Если слово «скорость» понимать в более широком смысле, то можно производную функции y = f ( x )по x считать скоростью изменения переменной y в точке x.

Поэтому понятие производной находит широкое применение при изучении скорости течения различных процессов (например, скорость охлаждения нагретого тела; скорость осуществления работы – мощность; скорость обесценивания оборудования и т. п.).

2. Таблица производных основных элементарных функций

Выпишем правила дифференцирования основных элементарных функций:

1) ( xa )′ = axa−1 ;

2) (a x )′ = a x lna , (e x )′ = e x ;

(loga x)′ =

в частности, (ln x)′ =

;

lna

(sin x)′ = cos x ;

5) (cos x)′ = −sin x ;

(tgx)′ =

;

7) (ctgx)′ = −

;

cos2 x

sin2 x

(arcsin x)′ =

;

9) (arccos x)′ = −

;

1 − x2

10) (arctgx)′ =

;

11) (arcctgx)′ = −

1 + x2

Приведённые результаты следуют непосредственно из определения производ-

ной. Выведем, например, правило дифференцирования степенной функции xa . Действительно,

1 +

∆x a

− 1

′

(x + ∆x)

− x

= lim

= x

lim

∆x

∆x→0

a ∆x

∆x

a−1

− 1 a

при ∆x → 0

= x

lim

= ax

∆x

∆x→0

3. Основные правила дифференцирования

1) Пусть u(x) и v(x) – дифференцируемые функции, а с – постоянная величина, тогда:

′

± v

′

(4.4)

(u ± v )

= u

(правило дифференцирования суммы (разности) функций);

(u v )′ = u′ v + u v′

(4.5)

(правило дифференцирования произведения функций), в частности

′

(4.6)

(c u)

= c u

т. е. постоянный сомножитель можно выносить за знак производной;

′

u′ v − u v′

(4.7)

(правило дифференцирования частного функций).

Пример 4.3. Найти производные функций:

1) y = 2 x4 +

−5 x −1 ; 2)

y = cos x lg x + ln10 10 x ;

3) y =

arcsin x

3 x

Решение. 1) Используя правила (4.4), (4.6) и табличную производную степен-

ной функции, получим:

′

−

′

y′ = (2 x4 )

−(5 x)′ −(1)′ = 2 (x4 )

+ x

3 −5

(x1 ) −0

3 x

= 8 x4−1 −

−

−1

−5 x1−1 = 8 x3 −

−

3 −5.

2) Используя правила (4.4), (4.5), (4.6) и табличные производные, получим: y′ =(cos x lg x)′ +(ln10 10 x )′ =(cos x)′ lg x +cos x (lg x)′ + ln10 (10x )′ =

=−sin x lg x +cos x 1x ln101 + ln2 10 10 x .

3) Используя правило (4.7) и табличные производные, получим:

	(arcsin x)′ x −arcsin x ( x )′		1			x −arcsin x		1
y′ =	(arcsin x)′ x −arcsin x ( x )′		=	1 − x	2	x −arcsin x	2	x	.
y′ =	(	x )	=			x			.
		2				x


2) Правило дифференцирования сложной функции.
Пусть функция u = u(x)	имеет производную u′x ,			а функция y = f (u) –
производную fu′ . Тогда сложная функция y = f (u(x))				имеет производную y′x ,
которая определяется по формуле:
	y′x = fu′ u′x .			(4.8)
Пример 4.4. Найти производные функций:
1) y = 3 1 − x2 ;	2) y =	101−x	− (arcsin 2 x )2 .

		cos 5 x

Решение. 1) Производная находится как производная сложной функции, задан-

, u = 1 − x2 .

ной цепочкой равенств:

f ( u ) = 3 u = u

−

(3 1 − x2 )

′

−2 x

Так как fx/

= fu/

ux/

3 (−2 x), то

3 3

(1 − x2 )

101−x

′

(

)

′

2) Имеем:

− (arcsin 2 x )

cos 5 x

(101−x )′ cos 5 x − 101−x (cos 5 x)′

− 2 arcsin 2 x (arcsin 2 x)′ =

(cos 5 x)2

101−x ln10 (1 − x)′ cos 5 x − 101−x (−sin5 x) (5 x)′

−

cos2 5 x

−2 arcsin 2 x

(2 x)′ =

1 − (2 x)2

−101−x ln10 cos 5 x + 5 101−x sin5 x

−

4 arcsin 2 x

cos

2 5 x

1 − 4 x2

3) Правило дифференцирования обратной функции.

Пусть у дифференцируемой функции y = f (x) производная f ′(x) ≠ 0 и

существует обратная функция x = f −1 ( y) . Тогда обратная функция также дифференцируема и справедлива формула:

x′y =	1	.	(4.9)

	y′x

Пример 4.5. Найти производную x′y обратной функции к функции

y = arcsin(2x )		−1,	π
	в точке M		6	.

Решение. Воспользуемся правилом дифференцирования обратной функции. Для этого сначала вычислим

y′x =

(2x )′ =

2x ln 2

, y′x (M ) =

2−1 ln 2

ln 2 .

1 −(2x )2

1 − 22 x

1 − 2−2

Согласно формуле (4.9) имеем x′y (M ) =

y′x (M )

ln 2

Этот пример можно решить другим способом – найти обратную функцию и затем продифференцировать её:

2 x = sin y x = log2 (sin y) x′y =						1	1	cos y =	ctgy	.
2 x = sin y x = log2 (sin y) x′y =						sin y	ln 2	cos y =		.
						sin y	ln 2		ln 2
	ctg	π		3
Отсюда x′y (M ) =	ctg	6	=	3	.
Отсюда x′y (M ) =	ln	2	=		.
	ln	2		ln 2

4) Правило дифференцирования функции, заданной параметрически.

Пусть система уравнений x = x (t ) , y = y (t ) , где x (t ) , y (t ) – дифферен-

цируемые функции и x′(t ) ≠ 0 , определяет у как дифференцируемую функцию от

х. Тогда производная этой функции также задаётся параметрически и может быть
найдена по формуле:	yt′
x = x (t ), y′x =		.	(4.10)

	xt′

			x = sin t
Пример 4.6. Найти				.
Пример 4.6. Найти	y / функции, заданной параметрически			.
	x		y = cos2 t

Решение. Так как xt′ = cos t , yt′ = 2 cos t (−sin t ) , то по формуле (4.10) име-
	y′	= −2 sin t	легко исключить
ем y′x = −2 sin t . В данном случае из системы x			легко исключить
	x = sin t
параметр t, поэтому yx/	= −2 x .

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015193.02 Кб31ZADAChI_1.doc
#
14.02.2015134.14 Кб66ZADAChI_V.doc
#
14.02.2015866.93 Кб199zadat-fkh.pdf
#
14.02.201515.12 Mб32zaginajlov-kvl.pdf
#
14.02.20151.33 Mб24zaicevVM_2.pdf
#
14.02.20151.25 Mб29zajcevVM.pdf
#
12.03.2016345.72 Кб28zarnitsina-e-g-mapp-549003aae0d37.pdf
#
14.02.20154.64 Mб56zarn_met_kp.pdf
#
14.02.2015527.89 Кб23zarn_met_lab.pdf
#
14.02.20152.32 Mб8Zaschita_ot_shuma_404.doc
#
14.02.201521.04 Mб34zrumov_inf_pos.pdf