
zajcevVM
.pdf
Неопределенности вида (∞ – ∞), (0 ∞) рекомендуется предварительно приводить путём тождественных алгебраических преобразований к
неопределенностям вида |
0 |
|
|
|
∞ |
||
|
|
|
или |
|
. |
||
0 |
|||||||
|
|
|
|
|
∞ |
||
Пример 3.20. Вычислить |
|
|
lim |
x2 + 2 x − x |
) |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x→+∞( |
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Неопределённость вида (∞ − ∞). |
Умножив и разделив выражение |
|||||||||||||||||||||||
x2 + 2 x − x на |
x2 + 2 x + x , |
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|||||||||
сведём неопределённость к виду |
, а затем |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
раскроем её: |
|
|
|
|
|
|
|
( |
|
x2 + 2 x − x) ( x2 + 2 x + x) = |
|
|
|
|
||||||||||
lim |
|
( |
x2 + 2 x − x) = lim |
|
|
|
|
|
||||||||||||||||
x→+∞ |
|
|
|
|
x→+∞ |
|
|
|
|
|
x2 + 2 x + x |
|
|
|
|
|
||||||||
= lim |
|
x2 + 2 x − x2 |
= lim |
|
|
|
|
2 x |
|
|
= |
|
x2 + 2 x ~ x |
= lim |
2 x |
= 1 . |
||||||||
|
|
x2 + 2 x + x |
|
|
|
|
|
|
|
|
|
|||||||||||||
x→+∞ |
|
x→+∞ |
|
x2 + 2 x + x |
|
|
|
x→+∞ 2 x |
|
|
|
|||||||||||||
Пример 3.21. Вычислить lim( x −1 ) ctgπ( x −1 ). |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Неопределённость (0 ∞). |
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||
Сведём неопределённость к виду |
|
|
: |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
lim( x −1 ) ctgπ( x −1 ) = lim |
|
|
x −1 |
1 ) |
= tgπ( x −1 ) ~ π ( x −1 ) |
= |
|
|
|
|||||||||||||||
x→1 |
|
|
|
|
x→1 tgπ( x − |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
= lim |
|
x −1 |
= 1 / π . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
π( x −1 ) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x − 3 2 x+1 |
|
|
|
|
|
|
|
|
|
|
||||
Пример 3.22. Найти lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x→∞ |
x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. |
Так |
как |
lim |
x − 3 |
= 1 , |
а lim ( 2 x + 1 ) = ∞ , |
то имеем предел, |
|||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
x→∞ x + 2 |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|||||
связанный с раскрытием неопределенности вида ( 1∞ ). Преобразуем её так, чтобы воспользоваться вторым замечательным пределом (см. (3.8)):
|
|
2 x+1 |
|
|
|
|
|
2 x+1 |
|
|
|
|
x+2 −5 |
( 2 x+1 ) |
||
x − 3 |
|
|
|
x − 3 |
|
|
|
−5 |
|
|
|
|||||
|
|
|
|
−5 |
x+2 |
|||||||||||
lim |
|
|
= lim |
1 |
+ |
|
− 1 |
|
= lim |
1 + |
|
|
|
|
|
= |
|
x + 2 |
x + 2 |
|
|
|
|||||||||||
x→∞ x + 2 |
|
x→∞ |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|||
71

|
|
|
−5 |
|
x+2 |
|
lim |
−10 x−5 |
|
|
−5 |
|
|||||
= lim |
1 |
+ |
|
|
|
= e |
= ex→∞ |
x+2 = e−10 . |
x + 2 |
|
|||||||
x→∞ |
|
|
|
|
|
|
|
9. Непрерывность функции. Точки разрыва
Пусть функция |
y = f (x) определена в точке x = x0 и в некоторой окрестности |
|
этой точки. Функция y = f (x) называется непрерывной в точке x0, |
если в этой |
|
точке существует |
конечный предел функции и он совпадает с её |
значением |
f (x0 ) , т. е. |
|
|
|
lim f ( x ) = f ( x0 ) . |
(3.10) |
|
x→x0 |
|
Итак, в точке x0 непрерывности функции f(x) должны быть выполнены следующие условия:
1)функция определена в точке x = x0 и в некоторой её окрестности;
2)существуют конечные односторонние пределы функции
lim f ( x ) = f ( x0 −0 ), |
lim f ( x ) = f ( x0 +0 ) ; |
x→x0 −0 |
x→x0 +0 |
3)односторонние пределы совпадают: f ( x0 −0 ) = f ( x0 +0 ) ;
4)совпадающие односторонние пределы функции в точке x0 равны значению функции в этой точке, т. е. f ( x0 −0 ) = f ( x0 +0 ) = f ( x0 ) .
Если функция непрерывна в каждой точке некоторой области, то она называется непрерывной в этой области.
Справедлива теорема: все элементарные функции непрерывны в области определения.
Если функция определена хотя бы в проколотой окрестности некоторой точки и не является в ней непрерывной, то говорят, что функция имеет разрыв в этой точке, а саму точку называют точкой разрыва функции.
Правило нахождения точек разрыва и выяснения характера разрыва функций.
1)Находим область определения и точки, в которых функция не определена, но в окрестности которых имеются бесконечное число точек области определения. Если функция задается несколькими формулами, то выделяем ещё точки перехода от одной формулы к другой.
2)Ищем пределы слева и справа в этих точках.
3)Если пределы справа и слева конечны и различны, то имеем разрыв 1-го рода. Если пределы равны, то разрыв устранимый. Во всех остальных случаях имеем разрыв 2-го рода (если хотя бы один из односторонних пределов равен бесконечности или не существует).
72
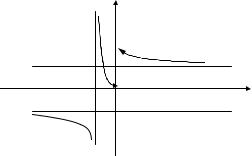
Пример 3.23. Исследовать функцию y = |
x |
+ |
1 |
на непрерывность. Найти |
|
|
|||||
x |
x + 1 |
||||
|
|
|
точки разрыва функции и определить их тип. Построить схематический график функции.
Решение. В точках x = 0 и x = – 1 функция не определена, так как знаменатели дробей обращаются в 0, а, значит, разрывна. Исследуем поведение функции вблизи этих точек, вычисляя односторонние пределы.
Заметим, что исходную функцию можно записать в виде:
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 + |
|
|
|
|
, |
|
если |
x > 0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
+ 1 |
|
|
|
|
. |
|
|
|
|
|
|||
|
|
f ( x ) = |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
−1 |
+ |
|
|
|
, |
если |
x < 0 |
|
|
|
|
|
|
||||
|
|
|
|
x + |
1 |
|
|
|
|
|
|
|||||||||
Для точки x = 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
f ( 0 −0 ) = lim |
|
−1 + |
|
= 0, |
f ( 0 +0 ) = |
lim |
|
1 |
+ |
|
= 2 . |
|||||||||
|
|
|
|
|
|
|||||||||||||||
x + 1 |
x + 1 |
|||||||||||||||||||
x→0−0 |
|
|
|
|
|
|
|
|
|
|
|
x→0−0 |
|
|
|
|
|
|||
Односторонние пределы функции в точке x = 0 существуют и конечны, но не равны между собой. Следовательно, эта точка является точкой разрыва 1-го рода.
Для точки x = – |
1: |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
||
f ( −1 −0 ) = −1 + |
|
lim |
|
|
|
= −∞, f ( −1 +0 ) = −1 + |
lim |
|
|
= +∞ .. |
||||||||
|
|
x + 1 |
|
x + 1 |
||||||||||||||
Итак, в точке x = – 1 |
|
x→−1−0 |
|
|
|
x→−1+0 |
|
|||||||||||
функция имеет разрыв 2-го рода. |
|
|
|
|
|
|
|
|||||||||||
Так как |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim f ( x ) = |
lim 1 |
+ |
|
|
|
|
=1, |
lim |
f ( x ) = lim |
−1 |
+ |
|
|
|
= −1 , |
|||
|
x +1 |
x +1 |
||||||||||||||||
x→+∞ |
x→+∞ |
|
|
|
|
|
|
x→−∞ |
x→−∞ |
|
|
|
|
|
||||
то схематический график функции имеет вид:
|
y |
|
|
2• |
|
|
1 |
y =1 |
–1 |
0 |
x |
|
–1 |
y = –1 |
73
|
|
1 |
|
|
|
, |
x < 1 |
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
||||
|
x + |
|
|
|
||||
Пример 3.24. |
|
|
|
|
|
|
|
1 ≤ x ≤ 2 найти точки разрыва, |
Для функции f ( x ) = x2 , |
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x > 2 |
|
|
|
|
|
|
|
||
|
e x−2 , |
|
||||||
|
|
|
|
|
|
|
|
|
указать характер разрыва, построить схематический график функции.
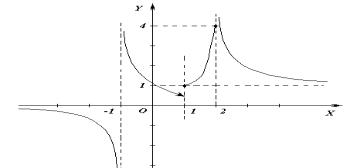
Решение. Данная функция составная и определена для всех действительных значений x ≠ −1 . Но нельзя сразу сказать, что она непрерывна для всех таких x. Разрывы могут быть в точках x = 1 и x = 2, где меняется ее аналитическое выражение. Итак, подлежат исследованию точки x = –1, x = 1, x = 2.
Исследуем точку x = – 1. Значение f(–1) не определено.
f ( −1 −0 ) = |
lim |
1 |
|
|
|
1 |
|
|
|
|
f ( −1+ |
0 ) = |
lim |
1 |
|
|
|
1 |
|||||||
|
|
= |
|
|
|
|
= −∞, |
|
|
|
= |
|
|
= +∞. |
|||||||||||
|
x→−1−0 |
x +1 |
|
|
−0 |
|
|
|
|
|
|
|
|
x→−1+0 |
x +1 |
|
|
+0 |
|||||||
Итак, точка x = – 1 является точкой разрыва 2-го рода. |
|
|
|
|
|
|
|
||||||||||||||||||
Исследуем точку x = 1. |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
f(1) = 12 = 1, |
f ( 1 − 0 ) = |
|
lim |
|
|
= |
, f ( 1 + 0 ) = |
lim |
x2 = 1 . |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x→1−0 x + 1 |
2 |
|
|
|
x→1+0 |
|
|
|||||||||
Итак, точка x = 1 является точкой разрыва 1-го рода. |
|
|
|
|
|
|
|
||||||||||||||||||
Исследуем точку x = 2. Имеем |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
f(2) = 22 = 4, |
|
|
|
|
|
|
|
|
x2 = 4 , |
|
|
|
|
|
|
|
|
= (e+∞ ) = +∞. |
|||||||
f ( 2 − 0 ) = lim |
f ( 2 +0 ) = |
lim e |
x−2 |
|
|||||||||||||||||||||
|
|
|
|
x→2−0 |
|
|
|
|
|
|
|
x→2+0 |
|
|
|
|
|
|
|
||||||
Итак, точка x = 2 – точка разрыва 2-го рода. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= e+0 = 1 + 0 , |
||
Так как lim |
f ( x ) = lim |
|
|
|
|
= −0 , а |
lim |
f ( x ) = lim e |
x−2 |
||||||||||||||||
|
|
|
|
1 |
|||||||||||||||||||||
x→−∞ |
x→−∞ x + |
|
|
|
x→+∞ |
|
x→+∞ |
|
|
|
|
|
|||||||||||||
то график данной функции имеет вид:
74
Варианты заданий контрольной работы № 3
3.1. Дана сложная функция y = f (u(v (x))) . Записать функции f(u), u(v), v(x). Составить сложную функцию v (u(x)).
1. |
y = cos |
4 |
1 |
|
|
2. |
|
y = e |
sin x |
|
|
|
3. |
y = lg(arccos x ) . |
||||||
|
|
|
. |
|
|
|
. |
|
|
|||||||||||
|
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = lg3 ( 1 |
− x2 ). |
|
|
|
|
|
1 |
|
|
y = log53 (lg x). |
|||||||||
4. |
5. |
|
y = 3 arctg |
|
. |
6. |
||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
7. |
y = |
|
|
1 |
|
. |
8. |
y = tg (4 ln x ) . |
|
9. |
y = ectg |
2 |
x . |
|||||||
cos(10 x ) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y = arcsin2 ( x ) . |
|
|
sin(3 x ) . |
|
|
|
1 |
|
|
||||||||||
10. |
11. |
|
|
|
12. |
y = 2 |
ln x |
. |
||||||||||||
13. |
y = arcctg (lg2 x) . |
14. |
1 |
|
. |
|
|
15. |
y = log02,1 (cos x). |
|||||||||||
|
3 cos(5 x ) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16. |
y = arctg( |
ln x ) . |
17. |
y = 2 arcsin x . |
|
|||||||||
19. |
y = sin |
3 |
|
1 |
20. |
y = 3 |
arccos(x |
2 ) |
|
|||||
|
|
|
|
. |
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
|
y = ln3 (arcsin x) . |
|
|
|
1 |
|
|
|
||||||
22. |
23. |
y = 4 tg |
|
|
|
. |
||||||||
x |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18. |
y = |
|
1 |
. |
|
log3 (lg x) |
|||||
21. |
y = |
tg ( x ) . |
|||
24. |
y = |
1 |
|
. |
|
sin(x3 ) |
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
y = 9cos |
2 |
|
|
|
|
|
|
|||||||||||
25. |
y = |
|
|
|
. |
|
26. |
y = |
arcsin |
|
|
|
|
. 27. |
|
x . |
|
|
|
|
|||||||||
cos3 |
(2x ) |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
28. |
y = log3 |
(sin x). |
|
29. |
y = |
|
1 |
. |
|
|
|
|
|
|
30. |
y = |
|
|
1 |
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
4 |
|
|
|
|
|
2 |
3 |
x |
|
|
|
|
|
|
|
|
|
arctg (e x ) |
|
|
|
||||||
3.2. Дана функция |
y = f (x). |
Найти |
обратную |
функцию |
y = f −1 (x) . |
||||||||||||||||||||||||
Указать области определения и множества значений этих функций. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
x+2 |
|
|
|
|
|
|
|
arcsin |
x |
|
|
3. f (x) |
|
|
1 − x 3 |
|||||||||
1. f ( x ) = log3 ( 2 |
|
− 4 ) . |
2. f ( x ) = 2 |
|
|
2 |
|
−1 . |
= |
|
|
|
. |
||||||||||||||||
|
|
|
|
1 + x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
75
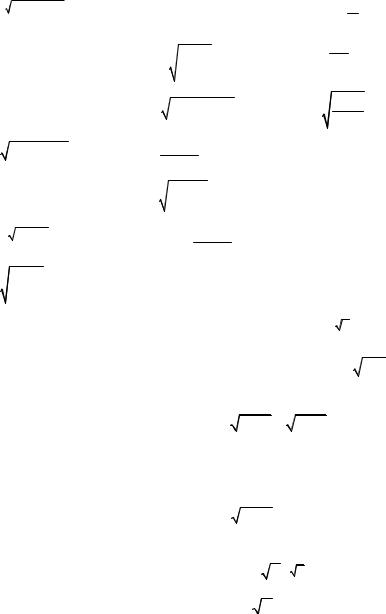
4. f ( x ) = 3 |
arc tg( x+1 ) . |
|
|||||
7. |
f ( x ) = |
arctg x + 1 |
. |
|
|
||
|
|
|
|||||
|
|
arctg x −1 |
|
||||
10. |
f ( x ) = |
|
|
arcsin x |
|
. |
|
|
arcsin x −1 |
||||||
|
|
|
|
||||
13. |
f ( x ) = 4 2arctgx −1 . |
||||||
16. |
f ( x ) = lg(arcsin x ) . |
||||||
19. |
f ( x ) = 4 |
2x +2 −8 . |
|
||||
5. f (x) = |
1 |
|
. |
|
lg (1 − 2 x) |
||||
8. f ( x ) = |
|
x −1 |
− 3 . |
|
|
x + 1 |
|||
|
|
|
|
|
6.f (x) = tg3 2 .
x
x+1
9.f ( x ) = 2 x−2 + 1 .
11.f ( x ) = lg( 3x + 1 ) .
14.f ( x ) = 4 x + 1 + 3 . 4 x −1
17. f ( x ) = 3 |
1 |
|
|
2 |
x |
−1 . |
|
20. f ( x ) = arctg 2 x +1 . 2x −1
12.f ( x ) = 3 11 +− xx + 1 .
15.f ( x ) = lg( 2 2 x+3 −1 ) .
18.f ( x ) = log3 ( 4 x −1 ) .
21. |
f ( x ) = |
arcsin x3 |
+ 1 |
. |
|
arcsin x3 |
−1 |
||||
|
|
|
|
f ( x ) = |
|
|
x + 2 |
|
|
x −1 |
|
. 24. f ( x ) = 2 |
log |
( x+2 ) |
|
|
22. |
4 |
|
|
. |
|
23. f ( x ) = arcsin |
|
|
3 |
|
. |
||
|
|
|
|
x + 1 |
|
|
x + 1 |
|
|
|
|
|
|
25. |
f ( x ) = |
|
2arcsin x+1 |
. |
26. f ( x ) = 3log5 ( 2x −2 ) . |
27. f ( x ) = lg( 4 |
x +1 + 1 ) . |
||||||
|
|
||||||||||||
|
|
2arcsin x + 1 |
|
|
|
30. f ( x ) = arctg ( |
lg x ). |
||||||
28. |
f ( x ) = arcsin( 2x −1 ) . 29. f ( x ) = 10log3 x+2 . |
|
|||||||||||
3.3. Вычислить пределы функций.
1. |
1) |
lim |
|
|
x2 −9 |
|
; |
|
|||
|
x2 |
|
|
|
|
|
|||||
|
|
x→3 |
|
− 4 x + 3 |
|
||||||
|
3) |
lim |
|
1 −cos 2 x |
; |
|
|
||||
|
|
|
3x2 |
|
|
|
|
||||
|
|
x→0 |
|
|
|
|
|
|
|
||
2. |
1) |
lim |
|
x |
2 −1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x→∞ 3x2 + 1 |
|
|
|
|
|
||||
|
3) |
lim |
arcsin 2 x |
|
; |
|
|
||||
|
|
|
|
||||||||
|
|
x→0 |
|
2 x2 − x |
|
|
|
||||
3. |
1) |
lim |
|
|
x2 −8 x + 15 |
; |
|||||
|
x2 |
−10 x + 21 |
|||||||||
|
|
x→3 |
|
||||||||
2) |
lim |
|
2 + x − |
|
2 − x |
; |
|||||
|
|
|
3x |
|
|
|
|||||
|
x→0 |
|
|
|
|
|
|
|
|||
|
lim |
x + 4 |
2 x |
|
|
|
|||||
4) |
|
|
|
|
. |
||||||
|
− 2 |
||||||||||
|
x→∞ x |
|
|
|
|
|
|||||
2) |
lim |
|
3 + x − 3 |
; |
|
|
|||||
|
x −6 |
|
|
||||||||
|
x→6 |
|
|
|
|
|
|||||
|
lim (1 − |
x ) |
2−x |
|
|||||||
4) |
|
x . |
|||||||||
|
x→+0 |
|
|
|
|
|
|
|
|||
2) |
lim |
|
x − |
x |
; |
|
|
|
|
||
|
x3 −1 |
|
|
|
|
||||||
|
x→1 |
|
|
|
|
|
|||||
76
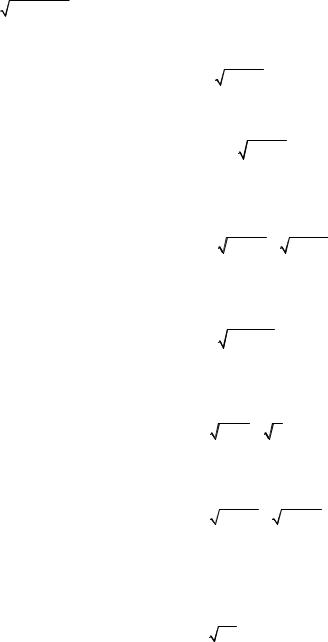
|
3) |
lim |
|
1 −cos 4 x |
; |
|
|
||||||||||
|
|
tgx |
|
|
|
|
|
|
|
|
|||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
1) |
lim |
|
3x3 + x2 −5 |
|
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x→∞ 2 x4 − x + 1 |
|
|
|||||||||||||
|
3) |
lim |
5−x −1 |
|
; |
|
|
|
|
|
|
|
|
|
|||
|
|
arctgx |
|
|
|
|
|
|
|
|
|
||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
||||
5. |
1) |
lim |
|
( x2 − 4 )2 |
|
|
|
; |
|
|
|||||||
|
x2 − 4 x + 4 |
|
|
||||||||||||||
|
|
x→2 |
|
|
|
|
|
||||||||||
|
3) |
lim |
cos x −cos3 x |
; |
|||||||||||||
|
|
ln2 (1 + 2 x) |
|
||||||||||||||
|
|
x→0 |
|
|
|
||||||||||||
6. |
1) |
lim |
|
2 x3 + x + 4 |
; |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x→∞ x4 − 2 x + 1 |
|
|
|
|
|||||||||||
|
3) |
lim |
|
x2 ctg5 x |
; |
|
|
|
|
|
|||||||
|
|
tg3x |
|
|
|
|
|
|
|
|
|||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
||||
7. |
1) |
lim |
|
x2 −6 x + 9 |
; |
|
|
|
|||||||||
|
( x2 −9 )2 |
|
|
|
|
|
|
||||||||||
|
|
x→3 |
|
|
|
|
|
|
|
|
|||||||
|
3) |
lim |
|
1 −cos 3x |
; |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x→0 |
|
1 −cos x |
|
|
|
|
|
|
|
|
|
||||
8. 1) |
lim |
|
5 − 3x |
|
|
; |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x→∞ x2 + x −5 |
|
|
|
|
|
|
|
||||||||
|
3) |
lim x2 ctg2 2 x ; |
|
|
|
|
|||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9. 1) |
lim |
|
x3 − 4 x |
|
|
|
; |
|
|
|
|||||||
x2 −5 x + |
6 |
|
|
|
|||||||||||||
|
|
x→2 |
|
|
|
|
|
|
|||||||||
|
3) |
lim |
|
|
1 −cos 4 x |
|
|
; |
|||||||||
|
|
x ln(1 + 2 x) |
|||||||||||||||
|
|
x→0 |
|
|
|||||||||||||
10. 1) |
lim |
|
3x2 + 4 |
; |
|
|
|
|
|
|
|
||||||
(2x −1)2 |
|
|
|
|
|
|
|
||||||||||
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
||||||
|
3x + 1 2 x |
||
4) lim |
|
. |
|
3x |
|||
x→∞ |
|
||
2) |
lim |
|
|
|
|
1 − x |
|
|
|
|
; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x→1 |
1 + 3x − 2 |
|
|
|
|||||||||||||||||||
4) |
lim( 1 − 2 x )1 / x . |
|
|
|
|||||||||||||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
lim |
|
|
3 − 9 − x2 |
|
|
|
|||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4) |
lim x ln |
x −1 |
. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x→∞ |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
lim |
|
1 + 2 x − |
|
|
|
|
|
1 − 4 x |
; |
|||||||||||||||
|
|
3x2 + x |
|
|
|||||||||||||||||||||
|
|
x→0 |
|
|
|
|
|||||||||||||||||||
4) |
lim (x + 1) |
|
|
2 |
|
|
|
. |
|
|
|
|
|||||||||||||
sin 4 x |
|
|
|
|
|||||||||||||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
lim |
1 − 3x2 −1 |
; |
|
|
||||||||||||||||||||
x3 + 2 x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
lim (1 − 2 sin x) |
1+x |
|
|
|
||||||||||||||||||||
4) |
|
|
|
x . |
|
|
|||||||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
lim |
|
|
|
|
|
x −1 − |
2 |
|
; |
|
|
|
|
|||||||||||
|
|
|
|
|
9 − x2 |
|
|
|
|
|
|
||||||||||||||
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
lim (2 − x) |
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
4) |
x−1 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
lim |
|
|
|
|
1 + 3x − |
|
2 x +6 |
; |
|
|||||||||||||||
|
|
|
|
x2 −5 x |
|
|
|||||||||||||||||||
|
x→5 |
|
|
|
|
|
|
|
|||||||||||||||||
|
lim |
|
2 x + 3 −x |
|
|
|
|
|
|
|
|
|
|||||||||||||
4) |
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||
2 x −1 |
|
|
|
||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2) |
lim |
|
|
|
|
|
x − 3 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3x − 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
77
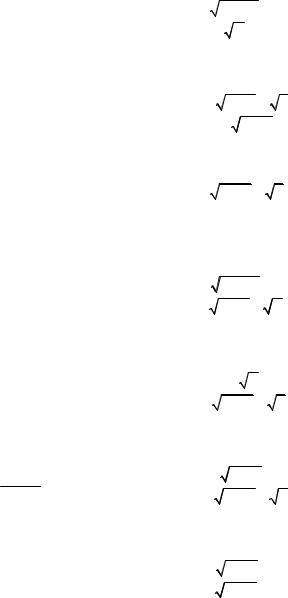
3) |
lim (e2 x −1) ctg3x ; |
|
||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. 1) |
lim |
|
4 x |
2 − x − 3 |
; |
|
|
|
|
|
|
|||||
|
|
|
x2 −1 |
|
|
|
|
|
|
|
|
|||||
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
lim |
3x |
2 − 2 x |
|
; |
|
|
|
|
|
|
|
|
|
||
|
sin 3x |
|
|
|
|
|
|
|
|
|
||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
||||
12. 1) |
lim |
|
( 2 x + 3 )2 − 25 |
; |
|
|||||||||||
|
3x2 −6 x + |
8 |
|
|
||||||||||||
|
x→∞ |
|
|
|
|
|||||||||||
3) |
lim |
cos2 2 x −1 |
; |
|
|
|
|
|
|
|||||||
|
x2 − 2 x |
|
|
|
|
|
|
|
|
|||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
||||
13. 1) |
lim |
3x |
2 − 2 x − 21 |
; |
|
|
||||||||||
|
x2 − 4 x + |
3 |
|
|
|
|
|
|||||||||
|
x→3 |
|
|
|
|
|
|
|
||||||||
3) |
lim |
|
sin(x − 2) |
|
; |
|
|
|
|
|
|
|||||
|
x2 − 3x + 2 |
|
|
|
|
|
|
|
||||||||
|
x→2 |
|
|
|
|
|
|
|
|
|
||||||
14. 1) |
lim |
|
x2 −7 x + 10 |
; |
|
|
|
|||||||||
|
|
4 − x2 |
|
|
|
|
|
|
|
|
||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
lim |
|
x3 + 4 x |
|
|
; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→0 l n(5 x + 1) |
|
|
|
|
|
|
|
|
|||||||
15. 1) |
lim |
|
2 x |
2 + 3x −5 |
|
; |
|
|
|
|
||||||
|
|
|
x2 −1 |
|
|
|
|
|
|
|
|
|
||||
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
lim (1 − x) ctg |
x2 −1 |
; |
|||||||||||||
|
||||||||||||||||
|
x→1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
16.1) lim 1 −5 x ; x→∞ 3x − 4
3) lim sin( x2 − 2 x ) ; x→0 tg( x2 + 3x )
17. 1) lim |
x2 |
− 4 |
; |
|
x2 − |
4 x + 4 |
|||
x→2 |
|
4) lim (3 − x)2 / (x−2) .
x→2
2) |
lim |
|
|
|
|
|
1 + 2 x − 3 |
; |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x→4 |
|
|
|
|
|
x − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim |
|
|
|
3x −10 x−3 |
|
||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||
|
3x + 2 |
|
||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2) |
lim |
|
|
|
|
|
1 − x − |
|
|
|
3 |
|
; |
|
||||||||||
|
|
|
|
|
x + 2 |
|
|
|
|
|
|
|
||||||||||||
|
x→−2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4) |
lim (4 − x) |
|
2 x |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x−3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
lim |
|
|
|
|
|
x + 3 − |
5 |
|
; |
|
|||||||||||||
|
|
|
|
|
x2 − 4 |
|
|
|
|
|
||||||||||||||
|
x→2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
lim |
|
7 x + 1 2 x+1 |
|
||||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x→∞ |
|
7 x −6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2) |
lim |
|
|
|
|
|
1 + 3x − 2 |
; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x→1 |
|
|
|
|
1 + x − |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x −1 |
||||||||
4) |
lim |
(x −1) ln |
|
|
|
|
|
|
|
|
. |
|||||||||||||
|
4 x + 3 |
|||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) |
lim |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
; |
|
|||||||
|
|
|
|
|
x + 3 − |
3 |
|
|||||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
lim |
x + 4 2 x+1 |
|
|||||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
. |
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
x→∞ |
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2) |
lim |
|
|
|
|
|
2 + x −1 |
; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x→−1 |
|
3 + x − |
|
|
|
2 |
|
|
|
||||||||||||||
|
lim (1 −5 x) |
2−x |
|
|
|
|
|
|
|
|
|
|||||||||||||
4) |
3 x |
. |
|
|||||||||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
lim |
|
|
|
|
|
3 + x −1 |
|
; |
|
|
|
|
|||||||||||
|
|
|
|
|
6 + x − 2 |
|
|
|
|
|
||||||||||||||
|
x→−2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
78
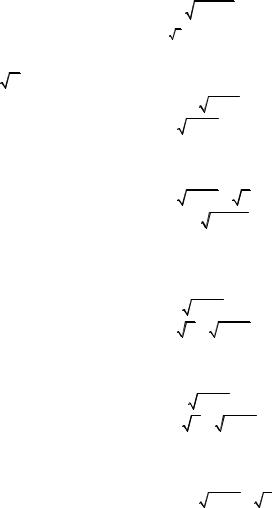
3) |
lim |
x2 − 2 x |
|
; |
|
|
|
|
|
|
|
|
|
|
|||
1 −e−2 x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
18. 1) |
lim |
2 x3 + x2 − 3 |
; |
|
|
||||||||||||
x3 + x − |
1 |
|
|
|
|
||||||||||||
|
x→∞ |
|
|
|
|
|
|
||||||||||
3) |
lim |
arcsin 4 x |
; |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
x→0 |
2 x + x |
|
|
|
|
|
|
|
|
|||||||
19. 1) |
lim |
|
|
|
x2 −1 |
|
|
|
; |
|
|
|
|
|
|
||
|
|
x2 + x − 2 |
|
|
|
|
|
|
|||||||||
|
x→1 |
|
|
|
|
|
|
|
|
||||||||
3) |
lim |
lg (3x + 1) |
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
x→0 |
x2 − 2 x |
|
|
|
|
|
|
|
|
|||||||
20. 1) |
lim |
2 x3 +6 x −5 |
|
; |
|
|
|||||||||||
x2 − x + |
2 |
|
|
|
|
|
|||||||||||
|
x→∞ |
|
|
|
|
|
|
||||||||||
3) |
lim |
sin(x2 ) |
|
|
; |
|
|
|
|
|
|||||||
(2x2 + x)2 |
|
|
|
|
|
||||||||||||
|
x→0 |
|
|
|
|
|
|
||||||||||
21. 1) |
lim |
|
|
2 x2 − 3x + 1 |
; |
|
|
||||||||||
|
1 − x4 |
|
|
|
|
|
|
||||||||||
|
x→1 |
|
|
|
|
|
|
|
|
||||||||
3) |
lim |
arc sin2 ( x2 − 4 x ) |
; |
||||||||||||||
x2 |
|
|
|
|
|
|
|
||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
||||||||
22.1) lim 7 − 2 x3 ;
x→∞ x2 + x
3) |
lim |
3−x −1 |
; |
|
|
||
|
|
|
|
||||
|
x→0 tg (x2 − x) |
|
|
|
|||
23. 1) |
lim |
2 x |
2 + x −10 |
; |
|
||
x2 |
−7 x + 10 |
|
|||||
|
x→2 |
|
|
||||
3) |
lim |
sin2 ( x2 − 3x ) |
; |
||||
(1 −102 x ) tg2 x |
|||||||
|
x→0 |
|
|||||
x − 2 |
3 x |
|
4) lim |
|
. |
|
||
x→∞ x + 1 |
|
|
2) |
lim |
|
|
|
x2 + 2 − 2 |
; |
|
|
|
|||||||||||||
|
|
|
|
|
x2 − 2 |
|
|
|
|
|
|
|
|
|
||||||||
|
x→ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
lim (1 + x2 ) |
5 x−1 |
|
|
|
|
|
|
||||||||||||||
4) |
|
x2 . |
|
|
|
|
||||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
lim |
2 − |
x + 1 |
; |
|
|
|
|
|
|
|
|||||||||||
|
|
x +6 − 3 |
|
|
|
|
|
|
||||||||||||||
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
lim |
|
5 x + 1 x+1 |
|
|
|
|
|
|
|||||||||||||
4) |
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||
5 x − 2 |
|
|
|
|
|
|||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) |
lim |
|
|
x + 3 − |
6 |
|
; |
|
|
|
||||||||||||
4 − |
x + 13 |
|
|
|
||||||||||||||||||
|
x→3 |
|
|
|
|
|
|
|||||||||||||||
|
lim (1 − 4 x) |
|
x+3 |
|
|
|
|
|
|
|||||||||||||
4) |
|
2 x |
. |
|
|
|
|
|
|
|
||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
lim |
|
|
|
x + 3 − 2 |
|
; |
|
|
|
||||||||||||
|
|
|
5 − x + 4 |
|
|
|
||||||||||||||||
|
x→1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
lim |
|
4 x −1 −x |
|
|
|
|
|
|
|||||||||||||
4) |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||
4 x + 1 |
|
|
|
|
|
|
|
|||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) |
lim |
|
|
|
|
x + 2 −1 |
|
|
; |
|
|
|
||||||||||
|
|
3 − |
|
x + 4 |
|
|
|
|
|
|||||||||||||
|
x→−1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
lim (1 − tg2 x) |
5 x+1 |
|||||||||||||||||||
|
4) |
|
|
|
x . |
|||||||||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2) |
lim |
|
|
x +7 − |
|
|
6 |
|
; |
||||||||||||
|
|
|
x2 + x |
|
|
|
||||||||||||||||
|
|
x→−1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
3x −7 − |
|
x |
+1 |
|
||||||||||
|
4) |
lim |
|
2 |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3x + 1 |
|
|
|
|
|
|
|||||||||||||||
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|||||||||||
79
24. 1) lim |
2 x2 − x −6 |
; |
||
x2 |
− 4 |
|||
x→∞ |
|
|||
3) |
lim |
|
sin2 |
x |
|
|
; |
|
|
|
|
||
(x2 − 4 x)2 |
|
|
|
|
|
|
|||||||
|
x→0 |
|
|
|
|
|
|
|
|
||||
25. 1) |
lim |
|
4 x2 |
−1 |
|
|
|
|
|
; |
|
|
|
|
2 x2 − 3x + |
|
1 |
|
|
|
|||||||
|
x→ |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3) |
lim |
arctg2 ( x2 − x ) |
; |
||||||||||
|
ln(1 |
− x |
2 |
|
) |
|
|
|
|||||
|
x→0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
26. 1) |
lim |
|
x2 +7 x −8 |
; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
x→∞ 2 x2 + x − 3 |
|
|
|
|||||||||
3) |
lim |
sin( x2 |
− 2 x ) |
; |
|
|
|||||||
|
x2 −6 x + 8 |
|
|
||||||||||
|
x→2 |
|
|
|
|
||||||||
27. 1) |
lim |
4 x2 − x − 3 |
|
; |
|
|
|
|
|||||
|
x2 + x |
− 2 |
|
|
|
|
|
|
|
||||
|
x→1 |
|
|
|
|
|
|
|
|
|
|||
3) |
lim |
arc sin( x2 − x ) |
; |
||||||||||
|
x2 |
−1 |
|
|
|
|
|
||||||
|
x→1 |
|
|
|
|
|
|
|
|||||
28.1) lim 2 x2 +7 x −9 ; x→∞ 3x2 + 4 x −7
3) |
lim |
tg( x |
2 − 4 x ) |
; |
|
|
|||||
x2 |
−16 |
|
|
|
|||||||
|
x→4 |
|
|
|
|
||||||
29. 1) |
lim |
x2 |
+ 3x −10 |
|
; |
|
|
||||
x2 |
+ |
4 x −12 |
|
|
|
||||||
|
x→2 |
|
|
|
|
||||||
3) |
lim |
|
sin2 ( x2 −5 x ) |
; |
|||||||
|
|
(43 x −1) |
|
|
|||||||
|
x→0 x |
|
|
|
|||||||
30. 1) |
lim |
x3 − x2 |
|
|
|
|
|||||
|
|
|
; |
|
|
|
|||||
|
|
|
|
|
|
||||||
|
x→∞ x2 |
+7 x −8 |
|
|
|
|
|||||
2) |
lim |
|
|
|
x +6 − 2 |
2 |
|
; |
|||||||||
|
|
|
3 − |
|
x +7 |
||||||||||||
|
x→2 |
|
|
|
|
|
|||||||||||
4) |
lim |
(1 + 2 x3 )ctg3 x . |
|||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
lim |
|
|
|
x +6 − 3 |
|
; |
|
|
||||||||
4 |
|
− |
|
|
|
|
|
|
|
|
|
||||||
|
x→3 |
|
x + 13 |
|
|||||||||||||
|
lim |
|
|
2 x + 3 4 x−1 |
|
||||||||||||
4) |
|
|
|
|
|
|
|
. |
|||||||||
|
2 x + |
1 |
|||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|||||||
2) |
lim |
|
|
|
x +7 − 3 |
|
; |
|
|
|
|
||||||
|
|
|
2 − |
x |
|
|
|||||||||||
|
x→2 |
|
|
|
|
|
|
|
|
|
|||||||
|
lim (3 − 2 x) |
2 x+1 |
|
||||||||||||||
4) |
|
x−1 |
. |
|
|
||||||||||||
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
lim |
|
|
|
x + 3 − |
6 |
; |
|
|
||||||||
|
2 |
− |
|
|
|
|
|
|
|
||||||||
|
x→3 |
|
2 x − 2 |
|
|||||||||||||
|
lim |
|
8 x −1 3 x |
|
|||||||||||||
4) |
|
|
|
|
|
. |
|
||||||||||
8 x + |
7 |
|
|
||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|||||||
2) |
lim |
|
|
|
1 + x |
2 |
|
− |
2 |
|
; |
||||||
|
|
|
3 − |
x + |
2 |
|
|||||||||||
|
x→1 |
|
|
|
|
|
|||||||||||
|
lim (5 x + 1) |
−2 x+1 |
|
||||||||||||||
4) |
|
|
3 x . |
||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
lim |
|
|
|
x + 8 − |
|
|
10 |
|
; |
|||||||
|
4 − |
|
x + 14 |
||||||||||||||
|
x→2 |
|
|
||||||||||||||
4) |
lim |
|
5 x − 3 −x+3 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
5 x + |
2 |
|
|
|
|
|
|
||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|||||||
2) |
lim |
|
|
x + 90 −10 |
; |
||||||||||||
|
|
7 − |
|
x + 39 |
|||||||||||||
|
x→10 |
|
|
||||||||||||||
80
