
zajcevVM
.pdf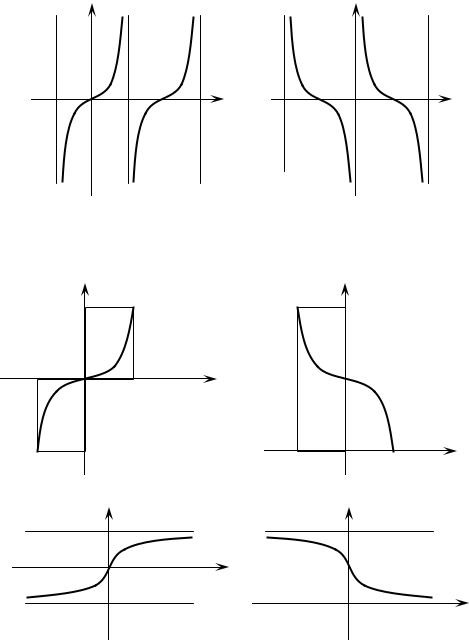
y |
y |
y = tg x |
y = ctg x |
– |
π |
0 π |
π |
x |
– π |
– |
π |
0 |
π |
π x |
2 |
2 |
|
|
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
Рисунок 7б
5) Обратные тригонометрические функции y = arcsinx, y = arccosx,
y = arctgx и y = arcctgx, называемые соответственно арксинусом, арккосинусом,
арктангенсом и арккотангенсом.
Нарисунках8а и8бпоказаны графикиобратныхтригонометрических функций.
|
y |
|
y |
|
|
π |
|
|
|
|
– |
y = arcsin x |
π |
|
|
2 |
|
||
|
|
|
π |
|
|
|
|
– |
|
– 1 |
0 |
1 |
2 |
y = arccos x |
x |
|
|||
π |
|
– 1 |
0 |
1 |
x |
- – |
|
|
|
|
|
2 |
Рисунок 8а |
|
|
|
|
|
|
|
|
|
|
y |
|
|
y |
|
|
π |
|
|
|
|
|
– |
|
|
|
|
|
2 |
y = arctg x |
|
|
|
|
|
|
π |
y = arcctg x |
|
|
0 |
x |
|
– |
|
|
|
2 |
|
|
π |
0 |
x |
- – |
||
2 |
|
|
|
Рисунок 8б |
|
61

Элементарными называются функции, получаемые из основных элементарных функций с помощью арифметических операций и суперпозиций (взятия функций от функций), примененных конечное число раз.
6. Понятие предела функции
При рассмотрении предела функции используется понятие окрестности точки.
Любой интервал (a, b), содержащий некоторую точку x0 числовой прямой, называется окрестностью этой точки и обозначается U( x0 ) . В частности,
интервал |
(x0 −δ , x0 +δ ) , где |
δ > 0 , называется δ - окрестностью точки x0 и |
|||||
обозначается Uδ ( x0 ) . Число x0 называется центром, а число δ – радиусом. |
|||||||
Если |
x (x0 −δ , x0 +δ ) , |
то выполняется неравенство |
x0 −δ < x < x0 +δ , |
||||
или, что |
то же, |
|
x − x0 |
|
<δ . |
Выполнение рассмотренных |
неравенств означает |
|
|
||||||
попадание точки x в δ - окрестность точки x0 .
Если из окрестности U( x0 ) исключить точку x0, то говорят о проколотой
окрестности U°( x0 ).
Множество Uδo ( x0 ) ={ x R : 0 < x − x0 <δ} называется проколотой δ -
окрестностью точки x0 .
Проколотые окрестности бесконечно удалённых точек +∞, –∞ и их объединения ∞ считаются совпадающими с окрестностями этих точек, т. е. при δ > 0
Uδo ( +∞) =Uδ ( +∞ ) ={x R : x > 1δ} = (1δ , + ∞), Uδo ( −∞) =Uδ ( −∞ ) ={x R : x < − 1δ}= (−∞, − 1δ ),
Uδo ( ∞) =Uδ ( ∞) ={x R : | x |> 1δ}= (−∞, − 1δ ) (1δ , + ∞).
Число b называют пределом функции f(x) в точке x0 и обозначают
b = lim f ( x ) , если для любой окрестности точки b найдётся такая проколотая
x→x0
окрестность точки x0, что любое число x из неё переводится функцией f(x) в окрестность точки b.
Это определение коротко можно записать так:
lim f (x) = b Uε (b) Uδo (x0 ) : x Uδo (x0 ) f (x) Uε (b) . (3.1)
x→x0
При обозначении предела иногда пишут f(x)→ b при x→ x0 и читают так: « f(х) стремится к b при x стремящемся к x0 ».
62

Это достаточно общее определение предела функции и в нём точки x0 и b числовой прямой не обязательно конечны. Важно лишь правильно выбрать окрестности, когда эти точки конечны и когда они таковыми не являются.
Например, для случая конечных x0 , b:
lim f (x) = b ε > 0 δ > 0 : 0 < x − x0 < δ f (x) − b < ε . (3.2)
x→x0
Если x→ x0 и при этом x < x0, то говорят, что x стремится к x0 слева и пишут x→ x0 – 0. Аналогично, если x→ x0 и x > x0, то x стремится к x0 справа и
пишут x→ x0 + 0. |
lim |
f ( x ) ≡ f (x0 −0) называют левосторонним пределом |
||
В таких случаях |
||||
x→x0 −0 |
|
lim f ( x ) ≡ f (x0 +0) – |
|
|
функции f(x) в точке |
x = |
x0, а |
правосторонним |
|
пределом. |
|
|
x→x0 +0 |
|
|
|
|
|
|
Справедлива теорема: |
предел функции существует тогда и только тогда, |
|||
когда существуют оба односторонних предела и они равны: |
|
|||
lim |
f (x) = b f (x0 −0) = f (x0 +0) = b . |
|
||
x→x0 |
|
|
|
|
Пример 3.9. Показать, что если |
f (x) = c , то lim f (x) = c . |
|||
|
|
|
x→x0 |
|
Решение. Действительно, x |
f (x) −c = c − c = 0 < ε , |
если ε – любое |
||
положительное число. Поэтому в качествеδ можно взять любое положительное число.
|
|
1, |
если x > 0, |
|
|
|
|
|
если x > 0, |
Пример 3.10. Показать, что составная функция знака sgn x = 0, |
||||
|
|
|
−1, если x > 0 |
|
|
|
|
||
не имеет предела в точке x0 = 0 . |
|
|
|
|
Решение. Вычислим односторонние пределы в данной точке: |
|
|
||
lim sgn x = lim |
(−1) = −1, |
|
|
|
x→0−0 |
x→0−0 |
|
|
|
lim sgn x = lim 1 = 1. |
|
|
||
x→0+0 |
x→0−0 |
|
|
|
Односторонние пределы не совпадают, поэтому lim sgn x не существует.
x→0
Сформулируем основные теоремы о пределах.
Теорема об единственности предела. Если существует предел функции при
х→ x0, то он единственный.
63
Теорема о пределе суммы, произведения и частного. Если существуют
конечные пределы lim = b1 , |
lim = b2 , то справедливы утверждения: |
x→x0 |
x→x0 |
lim ( f ( x ) ± g( x )) = b1 ± b2 ; |
|
||||||
x→x0 |
|
|
|
|
|
|
|
lim ( f ( x ) g( x )) = b1 b2 ; |
(3.3) |
||||||
x→x0 |
|
|
|
b1 |
|
|
|
lim |
f ( x ) |
= |
, |
( b ≠ 0 ) . |
|
||
g( x ) |
|
|
|
||||
x→x0 |
|
b |
2 |
|
|||
|
|
|
2 |
|
|
|
|
Замечание. Из последней теоремы следует, что:
1) постоянный сомножитель с можно выносить за символ предела, т. е.
|
|
lim (c f ( x )) = c lim f ( x ) ; |
|
|
|
x→x0 |
x→x0 |
2) lim ( f ( x )) |
n |
|
n |
|
= lim |
f ( x ) , n – любое целое число. |
|
x→x0 |
|
x→x0 |
|
Теорема о пределе элементарной функции. Предел элементарной функции в любой точке x0 её области определения равен значению функции в этой точке:
lim f ( x ) = f ( x0 ) .
x→x0
7. Предел числовой последовательности
Рассмотрим действительную функцию натурального аргумента, т. е. f(n) R,
n N. Такую функцию называют числовой последовательностью и обычно обозначают так:
xn = f(n) R, n N или {xn}, n N.
Числа x1 , x2 , x3 , …, xn , … называют элементами (или членами)
последовательности, символ xn – общим элементом последовательности, а число n
– его номером.
Формула, задающая величину xn , называется формулой общего элемента последовательности {xn} и она полностью определяет последовательность.
Например, последовательность {n2} задана формулой xn = n2. С помощью
этой формулы можно вычислить любой элемент этой последовательности: x1 = 12 = 1, x2 = 22 = 4, x5 = 52 = 25 и т. д.
Однако знание нескольких первых элементов последовательности ещё не определяет саму последовательность. Нужно ещё определить вид общего элемента.
Например, последовательность задана такими первыми элементами: 2, 10, 26,
82, 242, 730, … . Заметим, что 2 = 3 – 1, 10 = 32 + 1, 26 = 33 – 1, 82 = 34 +1 и
т. д. Итак, формула общего элемента xn = 3n +(–1)n.
64

Последовательность {xn} называется ограниченной сверху (снизу), если существует число M (число m) такое, что n N xn ≤ M (xn ≥ m) .
Последовательность {xn} называется ограниченной, если она ограничена и сверху и снизу. Условие ограниченности можно записать в виде:
C : xn ≤ C n N .
Дадим определение конечного предела последовательности.
Число b называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа ε можно указать такое натуральное число n0, что при всех n ≥ n0 элементы последовательности xn отличаются от b
меньше, чем на ε.
Это определение можно записать в символической форме:
b = lim xn ε > 0 n0 : n ≥ n0 |
|
xn − b |
|
< ε . |
(3.4) |
|
|
||||
n→∞ |
|
|
|
|
|
В общем случае n0 зависит от ε. Как правило, чем меньше ε, тем больше n0. Последовательность, для которой точка b является пределом, называют
сходящейся к этой точке.
|
Пример 3.11. Показать, что lim |
1 |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
n→∞ n |
|
|
|
|
|
|
|
1 |
|
|
|
||
|
Решение. При произвольном ε > |
0 предположим, |
|
что |
− 0 |
< ε . |
Тогда |
||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
n > |
|
1 |
. Если взять n |
= |
1 |
(целая часть числа |
1 |
), то утверждение будет верно |
|||||||||||
|
|
|
|
||||||||||||||||
|
|
ε |
0 |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|||
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|||||
по определению (3.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Дадим определение бесконечного предела для последовательности: |
|
||||||||||||||||
|
|
|
lim xn = ∞ ε > 0 n0 : n ≥ n0 |
|
xn |
|
> |
1 |
. |
|
(3.5) |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В отличие от сходящихся последовательностей, которые сходятся к конечному пределу, последовательности, которые имеют бесконечный предел (также, как и последовательности, не имеющие ни конечного, ни бесконечного предела)
называют расходящимися.
Пример 3.12. Показать, что lim |
( −1 )n n |
не существует, т. е. |
|
n + 1 |
|||
n→∞ |
|
( −1 )n n
последовательность расходится.
n + 1
Решение. В самом деле, если выбрать, например, ε = 1, то все элементы
65
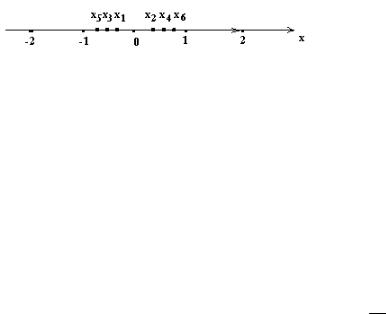
последовательности с чётными номерами попадают в ε – окрестность точки x = 1, а все элементы с нечётными номерами – в ε – окрестность совсем иной точки x = –1, причём эти окрестности не имеют общих точек (рисунок 6).
Рисунок 9
Но, по определению, если бы одна из точек x = 1 или x = –1 была пределом этой последовательности, то все её элементы, начиная с некоторого номера, должны были попасть в выбранную окрестность этой точки.
Если для последовательности {xn} справедливо неравенство xn ≤ xn+1 (в
частности, xn < xn+1 ) или xn ≥ xn+1 (в частности, xn > xn+1 ) n N, то её называют неубывающей (в частности, возрастающей) или невозрастающей (в
частности, убывающей). Последовательности всех этих типов, изменяющиеся в одном направлении, объединяются под общим названием монотонных (в частности, строго монотонных) последовательностей. В этом случае обычно говорят, что последовательность монотонно возрастает или монотонно убывает.
Для монотонных последовательностей имеет место важная теорема Вейерштрасса: монотонная ограниченная последовательность имеет конечный предел, т. е. сходится.
Пример 3.13. Доказать, что последовательность с общим элементом xn = nn!n
сходится.
Решение. Напомним, что n! = 1 2 3 ... ( n −1 ) n – факториал числа n. Достаточно показать, что данная последовательность монотонна и ограничена. Для
этого рассмотрим |
x |
n+1 |
= |
( n + 1 )! |
: |
n! |
= |
n!( n + 1 )nn |
= |
nn |
. |
|
|
(n + 1)n+1 |
nn |
(n + 1)n ( n + 1 )n! |
( n + 1 )n |
||||||
|
xn |
|
|
|
|
||||||
Так как |
nn |
< 1 , то xn+1 < xn , а это означает, что последовательность |
|
( n + 1 )n |
|||
|
|
монотонно убывает и ограничена сверху. Так как xn > 0, то она ограничена снизу, например, нулём. Следовательно, последовательность монотонна и ограничена. По теореме Вейерштрасса она сходится, т. е. имеет конечный предел.
8. Бесконечно малые и бесконечно большие функции
Функция α (x) называется бесконечно малой (б. м.) при x→ x0 , если |
|
lim α( x ) = 0 . |
(3.6) |
x→x0
Сумма конечного числа б. м. функций и произведение б. м. функций являются
66

б. м. функциями. Этого, вообще говоря, нельзя сказать о частном: деление одной б. м. на другую может привести к различным результатам, говорят, что имеется
0
неопределённость вида . В этом случае надо применять специальные приёмы
0
раскрытия неопределённости.
Пример 3.14. Найти lim |
x3 − x2 − x + 1 |
. |
||
x3 |
− 3x + 2 |
|||
x→1 |
|
|||
Решение. Убеждаемся, |
что |
предел нельзя найти непосредственной |
||
подстановкой вместо x величины 1, в данном случае имеем отношение двух б. м.
0
функций (неопределённость ).
0
Так как многочлены числителя и знаменателя дроби обращаются в ноль при x = 1, то, можно без остатка разделить эти многочлены на (x – 1):
_x3 – x2 – x + 1 |x – 1 |
|
|
|
|
_x3 – 3x + 2 |
|
|x – 1 |
|
||||||||||||||||||
x3–x2 |
|
|
x2 – 1 |
|
|
|
|
x3– x2 |
|
|
|
|
|
|
x2 + x – 2 |
|||||||||||
|
|
_–x+1 |
|
|
|
|
|
|
|
|
_x2–3x+2 |
|
|
|
|
|
|
|||||||||
|
|
|
–x+1 |
|
|
|
|
|
|
|
|
|
|
x2–x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
_–2x+2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2x+2 |
|
|
|
|
||||||
|
|
|
x3 |
− x2 − x + 1 |
|
|
x2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||
|
|
lim |
= lim |
− 1 |
= |
0 |
|
|
|
|
|
|
|
|
||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||
x |
3 − 3x + 2 |
|
|
x2 + x − 2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
x→1 |
|
|
x→1 |
|
0 |
|
|
|
|
|
|
|
|
|||||||||||
Снова аналогичная ситуация. Можно снова произвести деление, или разложить |
||||||||||||||||||||||||||
многочлены на множители: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
lim |
|
x2 − 1 |
|
= lim |
( x − 1 )( x + 1 ) |
|
= lim |
x + 1 |
|
= |
|
2 |
. |
|
|
|
||||||||||
|
x2 + x − |
2 |
( x − 1 )( x |
+ 2 ) |
x + 2 |
3 |
|
|
|
|||||||||||||||||
x→1 |
x→1 |
x→1 |
|
|
|
|
|
|||||||||||||||||||
Пример 3.15. Найти lim |
1 − x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x→1 |
1 − 3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
Решение. Убедившись, что имеет место неопределённость |
|
, умножим |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
числитель и знаменатель на произведение |
|
( 1 + |
|
x )( 1 + 3 x + 3 x2 ) и |
||||||||||||||||||||||
воспользуемся формулами разности квадратов и разности кубов |
|
|||||||||||||||||||||||||
(1 + x )(1 − x ) = 1 − x, (1 − 3 x )(1 + 3 x + 3 x2 |
) = 1 − x : |
|||||||||||||||||||||||||
67

lim |
1 − x |
= lim |
( 1 − x )( 1 + 3 |
x + 3 x2 ) |
= lim |
1 + 3 |
x + 3 x2 |
= |
3 |
. |
||
1 − 3 x |
( 1 − x )( 1 |
+ x ) |
|
1 |
+ x |
2 |
||||||
x→1 |
x→1 |
x→1 |
|
|
||||||||
Можно иначе решить эту задачу путем замены переменной. Полагая x=t6, получим t→ 1 при x→ 1, поэтому
lim |
1 − x |
= lim |
1 − t3 |
= lim |
( 1 − t )( 1 + t + t2 ) |
= lim |
1 + t + t2 |
= |
3 |
. |
||
1 − 3 x |
1 − t2 |
( 1 − t )( 1 + t ) |
|
1 + t |
2 |
|||||||
x→1 |
x→1 |
x→1 |
x→1 |
|
|
|||||||
При вычислении пределов часто используются два замечательных (из-за большого числа их приложений) предела:
1-й замечательный предел
lim sin x = 1
x→0 x
2-й замечательный предел
или lim |
sinα (x) |
= 1 ; |
(3.7) |
|
α (x) |
||||
α(x)→0 |
|
|
lim |
( |
1 + x |
) |
1 x = e или |
lim |
( |
1 +α |
( |
x |
)) |
1α(x) = e . |
(3.8) |
x→0 |
|
|
α(x)→0 |
|
|
|
|
Иррациональное число e = 2,71828... ≈ 2,72 называют неперовым числом. В
курсе математики важное значение имеют экспонента ex и натуральный логарифм ln x = loge x .
Две б. м. функции α (x) |
и β (x) при x→ x0 |
|
называются эквивалентными, |
||||||||||||||||||||
если lim |
α( x ) = 1 . Обозначение: |
α( x ) |
β( x ) при x→ x0. |
||||||||||||||||||||
x→x0 |
β( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот результат можно записать в виде эквивалентности sin x x при x→ 0. |
|||||||||||||||||||||||
Пример 3.16. Показать, что 1 −cos x |
|
|
x2 |
при x→ 0. |
|
||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
x 2 |
|
|||||
|
|
1 −cos x |
|
|
2 sin |
|
|
|
|
|
|
sin |
|
|
|
|
|
||||||
Решение. lim |
= lim |
|
|
2 |
|
= lim |
|
2 |
= 1 . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|||||||||||||
|
x→0 |
|
x2 |
x→0 |
x2 |
|
|
x→0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
Укажем важное свойство эквивалентных б. м.:
если α (x) α1 ( x), а β ( x) |
β1 |
( x) при x→ x0, то lim |
α( x ) |
= |
lim |
α1 |
( x ) |
. |
|
β( x ) |
β1 |
( x ) |
|||||||
|
|
x→x0 |
|
x→x0 |
|
68

Пусть α(x) – б. м. функция при x→x0. Приведем таблицу основных эквивалентностей, которая во многих случаях позволяет упрощать вычисление
пределов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) sinα (x) |
α (x) ; |
|
|
|
|
|
|
2) arcsinα ( x) |
|
|
α ( x) ; |
|||||||||||||||||||
3) tgα ( x) |
α ( x) ; |
|
|
|
|
|
|
|
4) arctgα ( x) |
|
α (x); |
|||||||||||||||||||
5) loga (1 +α (x)) |
α ( x) |
1 |
|
; |
|
|
6) aα(x) − 1 |
α ( x) lna ; |
||||||||||||||||||||||
lna |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7) ( 1 +α ( x) )a − 1 α (x) a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 3.17. Вычислить lim |
tgx − sin x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. |
|
|
|
|
|
x→0 |
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
sin x − sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
tgx − sin x |
0 |
|
|
|
|
|
|
|
sin x( 1 − cos x ) |
|
|||||||||||||||||||
|
|
cos x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
lim |
|
|
|
= |
|
= lim |
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||
|
x3 |
|
|
|
|
|
|
x3 cos x |
|
|
||||||||||||||||||||
x→0 |
|
0 |
|
x→0 |
|
x3 |
|
|
x→0 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
x |
x2 |
|
|
1 |
|
|
|
|
|||
= sin x |
x, 1 |
− cos x |
при x → 0 |
= lim |
|
|
2 |
|
= |
|
. |
|
|
|
||||||||||||||||
2 |
|
x3 cos x |
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
||||||||||
Полученный результат позволяет сделать вывод: tgx − sin x |
|
|
x3 |
при x→ 0. |
||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функция β (x) называется бесконечно большой (б. б.) при x→ x0 , если |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
lim β( x ) = ∞. |
|
|
|
|
|
|
|
|
|
|
|
(3.9) |
||||||||||
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Связь между б. б. и б. м. функциями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
если β (x) – б. б. функция при x→ x0, то |
|
1 |
|
|
– б. м. функция при x→ x0; |
|||||||||||||||||||||||||
|
β( x ) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
если α (x) – б. м. функция при x→ x0, то α(1x ) – б. б. функция при x→ x0.
Пусть |
α1 (x) ,α2 (x) – б. м., |
β1 (x), β2 |
(x) – б. б. при x→ x0, lim |
g( x ) = 1 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
Тогда при |
x→ x0 функции |
α1 , |
β1 |
, |
α |
1 |
β |
, |
β |
1 |
−β |
2 |
, |
gβ1 , β α1 , |
α α2 |
есть |
|
||||||||||||||||
|
|
α2 |
β2 |
|
|
1 |
|
|
|
1 |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
69

неопределённости соответственно вида |
|
||||||
0 |
∞ |
|
(0 ∞), |
(∞ − ∞), (1∞ ) , (∞0 ) , (00 ) . |
|||
|
|
, |
|
, |
|||
|
|||||||
0 |
∞ |
|
|
|
|
||
Неопределённость |
|
|
∞ |
раскрывается путём использования |
|||
|
вида |
|
|||||
|
|
|
|
|
|
∞ |
|
эквивалентных б. б. функций (определение и обозначение такое же, что и для б. м.).
Пример 3.18. Найти |
|
lim |
Pn ( x ) |
, где P (x) =a xn +a |
|
xn−1 +...+a x +a |
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x→∞ Qm ( x ) |
|
|
|
|
|
n |
|
|
|
n |
|
|
|
n−1 |
|
|
|
1 |
0 |
|||||||||||
|
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
и Q |
=b xm +b |
|
xm−1 |
+...+b x +b |
|
|
– многочлены |
степени n и |
m |
||||||||||||||||||||||||||||
m |
|
|
n |
|
|
m−1 |
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
соответственно (n, |
m – натуральные числа). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Решение. |
При x→ ∞ многочлены Pn(x) и Qm(x) – б. |
б. |
функции, поэтому |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
имеет место неопределённость |
. Поделим числитель и знаменатель данной |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞, если k > 0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
lim x |
k |
= |
|
|
|
|
|
< 0 : |
|
|
|
|
|||||||||||
дроби, например, на x и учтём, что |
|
|
|
0, если k |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, если k |
= 0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n < m |
|
|
|
|
|
|
|
|
|
|
a xn−m |
|
|
|
|
xn−m−1 + K + a x−m |
|
|
0 , |
|
||||||||||||||||||||
|
P ( x ) |
|
|
|
+ a |
|
|
a |
|
|
|||||||||||||||||||||||||||
lim |
n |
|
|
|
= lim |
|
n |
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
= |
|
n |
,n = m . |
|
|||||
|
|
|
|
|
bm + bm−1 x−1 + K + b0 x−m |
|
|
|
|
|
|||||||||||||||||||||||||||
x→∞ Qm ( x ) |
x→∞ |
|
|
|
|
|
|
|
|
bm |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞, n > m |
|
||
|
|
|
Pn( x ) |
|
|
|
|
|
|
|
|
|
an−1 |
|
|
1 |
|
|
|
|
|
a0 |
|
1 |
|
|
|
|
|
|
|
|
|||||
Так как lim |
= |
lim |
1 + |
|
|
|
+ |
K + |
|
= |
1 , то можно сделать |
||||||||||||||||||||||||||
|
|
|
x |
a |
|
xn |
|||||||||||||||||||||||||||||||
|
x→∞ |
|
a xn |
|
|
x→∞ |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||
важный вывод: многочлен при x→ ∞ эквивалентен своему старшему члену: |
|
||||||||||||||||||||||||||||||||||||
|
|
|
a xn +a |
|
xn−1 |
+...+a x +a |
|
|
a xn |
при x→ ∞. |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
n |
|
n−1 |
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 3.19. Вычислить |
lim |
|
|
1 −7 x2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 x2 + x |
−9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∞
Решение. Здесь неопределённость вида . Раскроем её, используя
∞
эквивалентные б. б. функции при x→ ∞ : |
|
|
|
|
||
lim |
1 −7 x2 |
= 1 −7 x2 ~ −7 x2 , 2 x2 |
+ x −9 ~ 2 x2 |
= lim |
−7 x2 |
= −3,5 . |
x→∞ 2 x2 + x −9 |
|
|
x→∞ |
2 x2 |
|
|
70
