zajcevVM

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(0 ≤ ε < 1) называется эксцентриситетом

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

1.25 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 145 6 7 8 9 10 11 12 13 14 > Следующая >>>

x − x1	=	y − y1	.	(2.13)

x2 − x1		y2 − y1

5) Уравнение прямой, проходящей через точку M0(x0, y0) с заданным угловым коэффициентом k:

y − y0 = k ( x − x0 ),

(2.14)

где k – тангенс угла наклона прямой с положительным направлением оси Ox.

Расстояние от точки M0(x0, y0) до прямой с уравнением Ax + By + C = 0

можно вычислить по формуле

r =

Ax0 + By0 + C

(2.15)

A2 + B2

Пример 2.5. Написать общее уравнение прямой L, положение которой на

плоскости определяется следующими способами:

M1( 1; − 2 ) L, nr ={3; − 1} L ;

M1( 2; 0 ) L, sr ={1; 3} || L ;

M1( 1; 1 ) L, M2 ( 0; − 1 ) L ;

M1( −1; 1 ) L,

( OX , L ) = 120o ;

M1( 2; − 4 ) L, L L1 , L1 : 3x −5 y + 2 = 0 .

Решение.

1) Согласно (2.10) получим:

3 ( x − 1 ) + ( −1 ) ( y − ( −2 )) = 0 3x − y − 5 = 0.

2) Запишем каноническое уравнение прямой, используя (2.11):

x − 2

y − 0

Получим общее уравнение: 3( x − 2 ) = y 3x − y − 6 = 0 .

Заметим, что прямые в случае 1) и 2) параллельны.

3) Воспользуемся (2.13):

x − 1

y − 1

x − 1

y − 1

2( x − 1 ) = y − 1 2x − y − 1 = 0 .

−1

−2

0 − 1

−1 − 1

4) Так как ( OX ,L ) = 120o , то угловой коэффициент прямой

k = tg120o = tg( 90o + 30o ) = −ctg30o = − 3 . Тогда, согласно

(2.14),

уравнение прямой имеет вид

y − 1 = − 3 ( x − ( −1 )) 3x + y + 3 − 1 = 0 .

r				r
5) Вектор n ={3; −5} L1 ,				а, значит, n L , поэтому этот вектор можно
взять в качестве направляющего вектора прямой L. Согласно (2.11), уравнение
прямой имеет вид:	x − 2	=	y + 4	или 5 x + 3 y + 2 = 0 .
			−5
3

7. Плоскость и прямая в пространстве

Всякая плоскость в декартовой прямоугольной системе координат Oxyz может быть задана уравнением 1-й степени (линейным) относительно переменных x, y, z :

Ax + By + Cz + D = 0	(2.16)
– общее уравнение плоскости, причём вектор nr ={A, B, C}	перпендикулярен

этой плоскости.

Плоскость в пространстве можно задать разными способами. Каждому из них соответствует определённый вид её уравнения.

1) Уравнение плоскости, проходящей через точку M0(x0, y0, z0) перпендикулярно вектору нормали nr ={A, B, C} :

A( x − x0 ) + B ( y − y0 ) + C (z − z0 ) = 0 .	(2.17)
2) Уравнение плоскости, проходящей через три заданные точки	M1(x1 , y1 , z1),
M2(x2 , y2 , z2) и M3(x3 , y3 , z3), можно записать в виде

x − x1 x2 − x1 x3 − x1

y − y1 y2 − y1 y3 − y1

z − z1

z2 − z1 = 0 . (2.18) z3 − z1

Угол между двумя плоскостями P1 и P2, имеющими нормальные векторы n1

и n2 , равен или дополняет до 180° угол между n1 и n2 , поэтому

cos (P ,P

) =

cos (n ,n

)

(2.19)

Расстояние от точки M0(x0 , y0 , z0) до плоскости, определяемой уравнением

Ax + By + Cz + D = 0, можно вычислить по формуле

r =

Ax0 + By0 + Cz0

+ D

(2.20)

A2 + B2 + C 2

Пример 2.6. Написать общее уравнение плоскости P, положение которой

определяется следующими способами:
		uuuuuur
	1)	M1 P , M1 M2 P , где M1 ( 3, − 1, 2 ), M2 ( 1, 3, 5 ) ;
	2)	M1 ( 1, −1, 2 ) P , P \|\| P1 , где P1 : x + y − 2z + 1 = 0 .
	Решение.
r	1) Используем уравнение (2.17). Так как x0 = 3,		y0 = –1, z0 = 2,
	uuuuuuuur	={1 − 3, 3 −( −1 ), 5 − 2} ={–2, 4, 3},
n = M1 M2			поэтому А = –2, В = 4, С = 3.

Получаем искомое уравнение плоскости:

–2(x – 3) + 4(y – (–1)) + 3(z – 2) = 0 или –2x + 4y + 3z + 4 = 0.

2) Вектор нормали nr ={1, 1, − 2}плоскости P1 также будет вектором нормали

и для плоскости P, так как P || P1. Уравнение плоскости P по точке M1 и вектору нормали n (формула (2.17)): (x – 1) + (y + 1) – 2(z – 2) = 0 x + y – 2z + 4 = 0.

Уравнения прямой в пространстве, проходящей через точку M0(x0, y0, z0)

параллельно направляющему вектору sr ={sx , sy , sz } :

x − x0

y − y0

z − z0

(канонические уравнения).

(2.21)

Уравнения (2.21) можно записать в виде параметрических уравнений:

x = x

+ s

t – параметр.

y = y0 + sy t ,

(2.22)

z = z

+ s

Уравнения прямой в пространстве, проходящей через две заданные точки

M1(x1, y1, z1) и M2(x2 , y2 , z2), записываются в виде

x − x1

y − y1

z − z1

(2.23)

− x

− y

− z

Пример 2.7. Даны координаты точек A1(2;– 3; 1), A2(–1; – 4; 2),

A3 (4; –1; 2), A4 (3; – 4; 2). Найти:

1)уравнение плоскости P1, проходящей через точки A1, A2, A3 и уравнение плоскости P2, проходящей через точки A1, A2, A4;

2)угол между плоскостями P1 и P2 ;

3)расстояние от точки A4 до плоскости P1 ;

4)уравнения прямой L1, проходящей через точки A1, A2;

5)уравнения прямой L2, проходящей через точку A4, перпендикулярно

плоскости P1;

6) координаты точки М0 (x0; y0; z0) пересечения прямой L2 с плоскостью P1.

Решение.

1) Уравнение плоскости P1 находим по формуле (2.18):

x −2 y +3 z −1

=−3(x −2)+5( y +3) −4(z −1) =0

−1−2 −4 +3 2 −1

−3

−1

4 −2 −1+3 2 −1

Поэтому 3 x − 5 y + 4z − 25 = 0 – уравнение плоскости P1.

Аналогично находится уравнение плоскости P2 :

x −2 y +3 z −1

=0(x −2)+4( y +3)+4(z −1) =0

−1−2 −4 +3 2 −1

−3

−1

3 −2 −4 +3 2 −1

−1

Поэтому

y + z + 2 = 0 – уравнение плоскости P2.

2) Плоскостям P1 и P2 соответствуют нормальные векторы

{3, − 5 , 4}, nr

{0, 1, 1}.

Находим угол между плоскостями, используя формулу (2.19):

r r

3 0 − 5 1 + 4

cos (P ,P ) =

cos (n ,n )

= 0,1 ,

32 + ( −5 )2 + 42 12 + 12

поэтому (P1 ,P2 ) = arccos(0,1) ≈ 84o .

3) При определении расстояния от точки A4(3; –4; 2) до плоскости P1, описываемой уравнением 3x – 5y + 4z – 25 = 0, обращаемся к формуле (2.20):

r =

Ax4 + By4 + Cz4 + D

3 3 + 5 4 + 4 2 − 25

6 2

A2 + B2 + C 2

32 + 52 + 42

4) Уравнения прямой L1, проходящей через точки A1 и A2, запишем по

формуле (2.23):

x − 2

y − ( −3 )

z − 1

поэтому

x − 2

y + 3

z − 1

–

−3

−1

−1 − 2

−4 − ( −3 ) 2 − 1

канонические уравнения прямой L1.

5) Вектор nr

={3, − 5, 4} P . Так как P

L n || L

, значит n –

направляющий вектор прямой L2. Согласно(2.21) получим канонические уравнения

прямой L2: x −3 3 = y−+54 = z −4 2 .

6) Точка M0(x0 , y0 , z0) – общая точка прямой L2 и плоскости Р1, поэтому для нахождения величин x0, y0, z0 необходимо решить систему уравнений:

x	0	− 3				y + 4			z	0	− 2
				=			0	=
	3						−5				4 .

3x		0	−5 y				+ 4z	− 25 = 0
					0		0

Проще всего решить эту систему, если от канонических уравнений прямой перейти к параметрическим:

x		− 3
	0		= t
		3	= t	x	= 3t + 3
		3		x	= 3t + 3
y		+ 4		0
	0		= t	y	= −5t − 4 .
			= t	y	= −5t − 4 .
	−5			z 0	= 4t + 2
z	0	− 2	= t	0
	0
		4
		4

Подставим величины x0, y0, z0 в уравнение плоскости P1:

3(3t + 3) − 5 (−5t − 4) + 4 (4t + 2) − 25 = 0 t = −0,24 .

Зная параметр t, легко определить точку М0:

x0 = 3(−0,24) + 3 = 2,28; y0 = −5(−0,24) − 4 = 2,8; z0 = 4(−0,24) + 2 = 1,04 . Итак, M0(2,28; 2,8; 1,04).

8. Линии второго порядка

Общее уравнение линии второго порядка имеет вид:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0,	(2.24)

где коэффициенты A, B и C одновременно в ноль не обращаются.

Может оказаться, что уравнение (2.24) определяет так называемую вырожденную линию (пустое множество, точку, прямую, пару прямых).

Если же линия невырожденная, то для неё найдётся такая прямоугольная декартова система координат, в которой уравнение этой линии имеет один из следующих трёх видов (каноническое уравнение):

x2	+	y2	= 1	,	(2.25)
a2		b2

x2	−	y2	= 1	,	(2.26)
a2		b2

y2 = 2 px .					(2.27)

При этом линия называется соответственно эллипсом, гиперболой, параболой.

Рассмотрим основные геометрические свойства этих линий на основе их канонических уравнений.

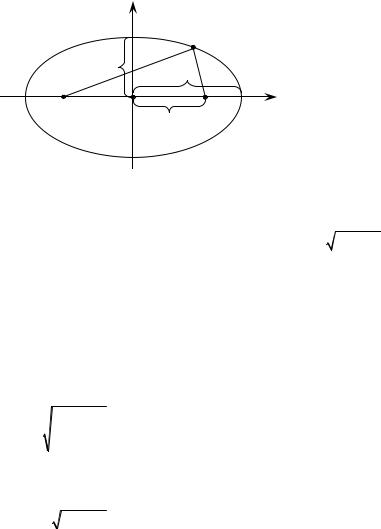
Эллипс с каноническим		уравнением				x2	+	y2	= 1, a ≥ b > 0 имеет вид,
Эллипс с каноническим		уравнением				a2	+	b2	= 1, a ≥ b > 0 имеет вид,
изображённый на рисунке 1.						a2		b2
изображённый на рисунке 1.
			y	B2
				B2			M(x, y)
							M(x, y)
		b		r1 a			r2
A1	F1		0				F2		x
A1	F1		0		с		F2		A2
					с

Рисунок 1

Величины a и b называются полуосями эллипса, точки A1(–a, 0), A2(a, 0),

B1(0, –b), B2(0, b) – его вершинами. Точки F1(–c, 0), F2(c, 0), где c =	a2 − b2 ,
называются фокусами эллипса, ось Ox, на которой располагаются фокусы,
называется фокальной осью, а числа r1 = F1 M , r2 = F2 M – фокальными
радиусами точки M, принадлежащей эллипсу.
Для всех точек эллипса справедливо равенство r1 + r2 = 2a ,	т. е. сумма

расстояний каждой точки эллипса до фокусов постоянна и равна большей оси.

В частном случае a = b фокусы F1 и F2 совпадают с центром О, а каноническое уравнение в этом случае можно записать в виде x2 + y2 = a2 , т. е. описывает окружность радиуса a с центром в начале координат.

эллипса и характеризует форму (степень сжатия) эллипса (при ε = 0 эллипс является окружностью).

Если в уравнении (2.25) a < b, то фокальной осью этого эллипса является ось

Oy. В этом случае c = b2 − a2	, ε =	c	.
Oy. В этом случае c = b2 − a2	, ε =		.
		b
Гипербола с каноническим	уравнением			x2	−	y2	= 1, a > 0, b > 0	имеет
Гипербола с каноническим	уравнением			a2	−	b2	= 1, a > 0, b > 0	имеет
				a2		b2

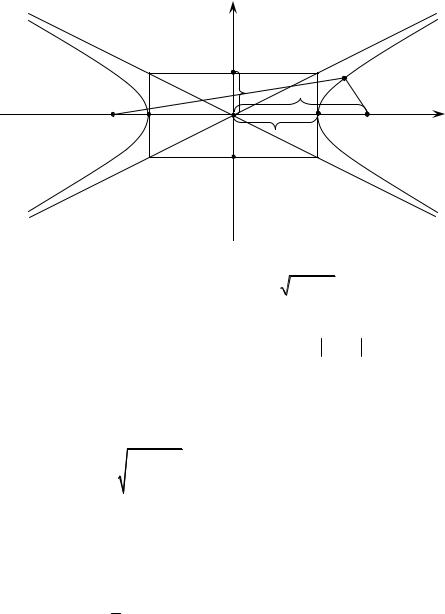
вид, изображённый на рисунке 2.

y = – –– x a

F1 A1

	y		b
	y		y = –– x
			a
	B2		M(x, y)
	r1		M(x, y)
	b	c	r2
0		A2	x
0	a	A2	F2
	a
	B1

Рисунок 2

Величины a и b называются полуосями гиперболы, точки A1(–a, 0), A2(a, 0) – её вершинами. Точки F1(–c, 0), F2(c, 0), где c = a2 + b2 , называются фокусами гиперболы, а числа r1 = F1 M , r2 = F2 M – фокальными радиусами точки M, принадлежащей гиперболе.

Для всех точек гиперболы справедливо равенство r1 − r2 = 2a , т. е. модуль

разности расстояний каждой точки гиперболы до фокусов есть величина постоянная, равная расстоянию между вершинами.

Оси Ox и Oy называются действительной и мнимой осями соответственно.

Прямые	y = ±		b	x	являются асимптотами гиперболы.

			a
		c			b	2
Число	ε =		=		1 +	(1 < ε < ∞) называется эксцентриситетом
		a
					a

гиперболы и характеризует форму (степень сжатия) гиперболы.

Уравнению

−

= 1

будет соответствовать также

гипербола.

Только

Oy, а

мнимой

–

Ox.

Её

фокусы

действительной

осью

будет

ось

F1 ( 0, −c ), F2 ( 0,c )

и вершины

B1 ( 0,b ) ,

B2 ( 0,b )

лежат

на оси

OY, а

эксцентриситет ε = bc . Построение такой гиперболы аналогично.

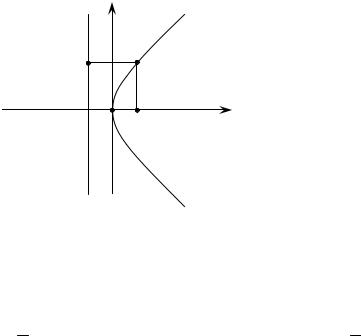
Парабола с каноническим уравнением y2 = 2 px, p > 0 имеет вид, изображённый на рисунке 3.

M(x, y)

, 0

x = −

Рисунок 3

Число p называется параметром

параболы,

точка F

, 0

– фокусом

параболы, число r = FM – фокальным радиусом точки М параболы, точка О –

вершиной параболы, а ось Ox – осью (фокальной) параболы.

Прямая L : x = − 2p , перпендикулярная оси и проходящая на расстоянии 2p

от вершины параболы, называется её директрисой.

Для всех	точек М параболы справедливо равенство	r = ρ (M , L) , где
ρ (M , L) –	расстояние от точки М до директрисы L,	т. е. каждая точка

параболы одинаково удалена от фокуса и директрисы.

Если в уравнении (2.27) поменять местами x и y, то уравнению x2 = 2 py

будет соответствовать также	парабола			с осью симметрии		Oy.			Парабола будет
располагаться над осью Ox,							p
	фокусом			будет точка F	0,			,	директрисой –
	фокусом			будет точка F	0,			,	директрисой –
							2
прямая, заданная уравнением	y = −	p	.
прямая, заданная уравнением	y = −		.
	2

В дальнейшем будет рассмотрен только частный случай (В = 0) уравнения

(2.24):

Ax2 + Cy2 + Dx + Ey + F = 0.

Такое уравнение может быть преобразовано к каноническому виду с помощью

параллельного переноса осей координат по формулам

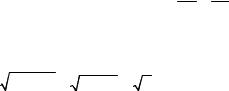
x		= x − x	x = x		+ x	(2.28)
	1	0	или	1	0 ,	(2.28)
y1 = y − y0			y = y1 + y0

где (x0, y0) – координаты нового начала O1 (в старой системе координат). Новые оси O1x1 и O1y1 параллельны старым. Приведение уравнения к каноническому виду удобно делать методом выделения полных квадратов. Рассмотрим этот метод на примере.

Пример 2.8. Уравнение линии второго порядка

9x2 + 16y2 – 90x + 32y + 97 = 0

привести к каноническому виду. Определить тип и расположение этой линии, характерные параметры. Сделать рисунок.

Решение. Группируем члены, содержащие только x и только y:

(9x2 – 90x) + (16y2 + 32y) + 97 = 0.

Выносим за скобки коэффициенты при x и y :

9(x2 – 10x) + 16(y2 + 2y) + 97 = 0.

Дополняем выражения в скобках до полных квадратов:

9(x2 – 10x + 25 – 25) + 16(y2 + 2y + 1 – 1) + 97 = 0, 9[(x – 5)2 – 25] + 16[(y + 1)2 – 1] + 97 = 0,

9(x – 5)2 – 225 + 16(y + 1)2 – 16 + 97 = 0,

9(x – 5)2 + 16(y + 1)2 – 144 = 0.

Введём новые пеpеменные (см. фоpмулы (2.28)):

x1 = x − 5		x = x1	+ 5	.
	= y + 1		− 1
y1		y = y1

Последние выражения определяют параллельный перенос осей координат в точку O1(5; –1). В новой системе координат O1x1y1 уравнение запишется в виде

9x12 + 16 y12 − 144 = 0

или (после переноса вправо свободного члена и деления на него) в канонической форме

x12 + y12 = 1 .

16 9

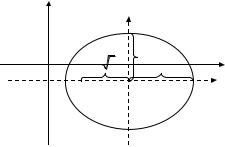
Итак, заданная линия второго порядка представляет собой эллипс с полуосями a = 4, b = 3. Центр эллипса находится в новом начале координат O1(5; –1), а его фокальная ось есть ось O1x1. Расстояние фокусов от центра

c = a2 − b2 = 16 − 9 = 7 .

Делаем рисунок.

		y1
0	c=	7	b=3
			a=4	x
	●
–1			●	x1
	F1	О1(5,–1) F2

Варианты заданий контрольной работы № 2

2.1. Даны координаты вершин треугольника ABC. Найти:

1)косинус угла BAC;

2)уравнение прямой L1, проходящей через точки A и С;

3)уравнение высоты L2, опущенной из вершины B на сторону AC;

4)координаты точки D пересечения прямых L1 и L2 .

1.	A ( 2; 1), B (– 1; 3), C ( 4; 5).	2.	A ( 1; 2), B ( 4; 2), C ( 3; – 2).
3. A ( 0; 2), B (– 2; 0), C (– 3; 4).		4.	A ( 1;– 2), B (– 2; 1), C ( 2; 4).
5. A (0; 2), B (– 2; – 2), C (1; 1).		6.	A ( – 2; 0), B ( 2; 4), C ( 4; 2).
7. A ( 1; 3), B ( 3; 5), C ( 5; – 3).		8.	A (– 2; 4), B (2; 2), C (0; – 2).
9. A(– 2; 4), B ( 3; 2), C ( 5; – 6).		10.	A (– 2; 1), B (– 4; 3), C (0; 5).
11.	A (1; 0), B ( 3; 2), C (0; – 4).	12.	A (– 2; 4), B (– 4; 0), C (2; 4).
13.	A (– 3; 0), B (1; – 2), C (– 2; 5).	14.	A (1; 3), B (3; 1), C (4; 5).
15.	A (2; 4), B (8; 0), C (0; – 2).	16.	A (– 1; – 4), B (– 2; 0), C (2; 2).
17.	A (4; – 2), B (1; 1), C (9; 2).	18.	A (1; 5), B (3; – 1), C (– 3; – 1).
19.	A (– 1; 2), B (– 3; 0), C (– 6; 4).	20.	A (2; – 1), B (0; 3), C (4; 5).
21.	A (1; 1), B (3; – 1), C (– 1; 2).	22.	A (4; 1), B (2; – 1), C (6; 0).
23.	A (– 1; 4), B (1; – 2), C (– 4; 2).	24.	A (– 1; 3), B (– 3; – 1), C (0; 3).
25.	A (1; 5), B (3; 1), C (– 1; 0).	26.	A (6; 2), B (2; 0), C (4; – 2).
27.	A (1; 3), B (– 1; 1), C (– 3; 4).	28.	A (2; 2), B (– 2; 0), C (1; – 1).
29.	A (4; 1), B (– 1; 1), C (5; 3).	30.	A (0; – 2), B (3; 0), C (2; – 4).

2.2. Даны координаты вершин пирамиды A, B, C, D. Найти:

1)площадь гpани ABC;

2)объём пиpамиды ABCD;

3)уравнение плоскости P1, содержащей грань ABC;

<<< < Предыдущая 1 2 3 45 / 145 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015193.02 Кб31ZADAChI_1.doc
#
14.02.2015134.14 Кб66ZADAChI_V.doc
#
14.02.2015866.93 Кб199zadat-fkh.pdf
#
14.02.201515.12 Mб32zaginajlov-kvl.pdf
#
14.02.20151.33 Mб24zaicevVM_2.pdf
#
14.02.20151.25 Mб29zajcevVM.pdf
#
12.03.2016345.72 Кб28zarnitsina-e-g-mapp-549003aae0d37.pdf
#
14.02.20154.64 Mб56zarn_met_kp.pdf
#
14.02.2015527.89 Кб23zarn_met_lab.pdf
#
14.02.20152.32 Mб8Zaschita_ot_shuma_404.doc
#
14.02.201521.04 Mб34zrumov_inf_pos.pdf