
zajcevVM
.pdf
знак f ′( x )«+»−1 «−» 0 «−» 1 «+» x
Итак, функция возрастает на интервалах ( −∞,−1), (1,+∞) и убывает на интервалах ( −1;0 ) и (0; 1).
4.2. Экстремум функции.
Если существует такая окрестность точки х0, что для всякой точки x ≠ x0
этой окрестности выполняется неравенство f (x) ≥ f (x0 ) ( f (x) ≤ f (x0 )) , то
точка х0 называется точкой минимума (максимума) данной функции.
Для обозначения максимума или минимума используется объединяющий их термин – экстремум.
Правило исследования функции на экстремум:
1)найти критические точки функции;
2)определить знак f ′(x) слева и справа от каждой критической точки. Если
при переходе аргумента х через критическую точку х0 (слева направо): |
||||||||||||
f ′(x) |
меняет знак с «−» |
на «+», то х0 |
– точка минимума; |
|||||||||
f ′(x) |
меняет знак с «+» на «–», то х0 |
– точка максимума; |
||||||||||
f ′(x) |
не меняет знака, то в точке х0 нет экстремума. |
|||||||||||
Иногда проще исследовать критические точки х0, если f ′′(x ) существует, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
пользуясь другим правилом, с помощью 2-ой производной: |
||||||||||||
если |
f ′′(x |
) > 0 , то х0 |
– точка минимума; |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
если |
f ′′(x |
) < 0 , то х0 |
– точка максимума; |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
если |
f ′′(x |
) = 0 , то требуются дополнительные исследования. |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Пример 5.5. |
Исследовать на экстремум функцию f ( x ) = 2 x + 3 3 x2 . |
|||||||||||
Решение. Функция определена и непрерывна при всех x. Производная |
||||||||||||
f ′( x ) = 2 + 3 |
2 |
x |
−1 |
3 = 2 |
|
1 + |
1 |
|
|
|||
|
|
|
|
не существует в точке x1 = 0 и обращает- |
||||||||
3 |
|
3 x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
ся в ноль при x2 = − 1. Отметим эти критические точки на числовой оси и определим знак f ′( x ) на полученных интервалах (см. рисунок).
111

знак f ′( x ) «+» −1 «−» 0 «+» x
Нетрудно убедиться, что lim f ′( x ) = ∞ (касательная к графику функции в его
x→0
точке О(0; 0) вертикальна).
Итак, точка x2 = − 1 − точка максимума, максимум f(−1) = 1; точка x1 = 0 − точка минимума, минимум f(0) = 0.
На рисунке показаны также интервалы возрастания и убывания функции.
4.3. Выпуклость, вогнутость, точки перегиба графика функции.
График функции y = f (x) называется выпуклым (вогнутым) на (a,b) , если график на этом промежутке расположен ниже (выше) касательной, проведенной к графику данной функции в любой точке x (a,b) .
Точка (x0 , f (x0 )) графика функции y = f (x) , отделяющая выпуклую его часть от вогнутой, называется точкой перегиба.
Точки, в которых f ′′(x) = 0 или не существует, называются критическими
точками 2-го рода.
Для функции f ( x ) , дважды непрерывно дифференцируемой на ( a,b ) , вер-
но утверждение (необходимый и достаточный признак выпуклости и вогнутости):
график функции f ( x ) выпуклый (вогнутый) на ( a,b ) тогда и только тогда, когда
f ′′( x ) ≤0 |
( f ′′( x ) ≥0) x (a,b ) . |
y = f (x) , то х0 – кри- |
Если |
х0 – абсцисса точки перегиба графика функции |
|
тическая точка 2-го рода (необходимый признак). |
x = x0 меняется знак |
|
Если при переходе через критическую точку 2-го рода |
||
второй производной, то точка кривой y = f (x) с абсциссой х0 является точкой
перегиба (достаточный признак).
Отсюда вытекает следующее правило отыскания интервалов выпуклости и вогнутости, а также точек перегиба графика функции y = f ( x ):
1)находим f ′′( x ) ;
2)находим точки, в которых f ′′( x ) равна нулю или не существует (критические точки 2-го рода);
3)определяем знак f ′′( x ) в каждом из промежутков, на которые область оп-
ределения функции разбивается найденными точками;
112
4) применяем достаточные признаки выпуклости и вогнутости, существования точек перегиба, находим их координаты.
Пример 5.6. Определить промежутки выпуклости и вогнутости, точки перегиба графика функции f ( x ) = xe−x .
Решение. Функция определена при всех значениях x. Вычислим производные: f ′(x) = (xe−x )′ = e−x + xe−x (−1) = (1 − x)e−x ,
f ′′(x) = ((1 − x)e−x )′ = −e−x +(1 − x)e−x (−1) = (x − 2)e−x .
Производная 2-го порядка существует при всех значениях аргумента. Найдём критические точки 2-го рода: f ′′( x) = 0 (x − 2)e−x = 0 x = 2 . Так как e−x > 0 при всех x, то f ′′(x) < 0 при x < 2, f ′′(x) > 0 при x > 2.
Итак, на интервале (−∞; 2) график функции выпуклый, на интервале (2; +∞) – вогнутый. При x = 2 график осуществляет перегиб (вторая производная меняет знак при переходе через x = 2), точка (2; 2e−2) – точка перегиба.
4.4. Асимптоты графика функции.
Прямая L называется асимптотой графика функции y = f (x) , если рас-
стояние точки кривой от прямой L стремится к нулю при неограниченном удалении указанной точки по графику от начала координат (т. е. при стремлении к бесконечности хотя бы одной из координат точки).
Если хотя бы один из пределов |
|
lim |
f (x) =∞ , |
то прямая x = a является |
||||||||||||||
вертикальной асимптотой. |
|
x→a±0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Прямая |
y = kx + b является |
наклонной |
асимптотой |
|
графика |
функции |
||||||||||||
y = f (x) , если существуют конечные пределы |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
k = lim |
f (x) |
, |
b = lim |
( |
f |
( |
x |
) |
− kx |
) |
. |
(5.6) |
|||||
|
|
|||||||||||||||||
|
x→∞ |
x |
|
|
x→∞ |
|
|
|
|
|
|
|||||||
При k = 0 имеем горизонтальную асимптоту |
y = b . |
|
|
|
|
|||||||||||||
Пример 5.7. Найти асимптоты графика функции |
|
y = |
|
e x |
. |
|
|
|
||||||||||
|
|
|
x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. |
Функция определена и непрерывна при всех x , за исключением |
|||||||||||||||||
x = 0 ( x = 0 |
– точка разрыва). Так как |
lim |
e x |
= ±∞ , то прямая с уравнением |
||||||||||||||
x |
||||||||||||||||||
|
|
|
|
x→0±0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
113 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||

x = 0 (ось Oy ) – вертикальная асимптота (двусторонняя).
Ищем наклонные асимптоты в виде y = kx + b . Для данной функции нужно
отдельно рассмотреть случаи x → +∞ и x → −∞ . Согласно (5.6) имеем
k = |
lim |
y |
= |
lim |
e x |
|
∞ |
= |
правило Лопиталя = |
lim |
ex |
|
∞ |
= |
|
|
= |
|
|
= |
|
||||||||
|
x→+∞ x |
|
x→+∞ x2 |
|
∞ |
|
|
x→+∞ 2 x |
|
∞ |
|
|||
= правило Лопиталя |
= lim |
|
e x |
= +∞ . Так как предел не конечен, то пра- |
||||||||||||||
|
|
|
|
x→+∞ 2 |
|
|
|
|
|
|
|
|
|
|
||||
восторонней наклонной асимптоты нет. |
|
|
|
|
|
|
|
|
|
|
||||||||
Ищем левостороннюю наклонную асимптоту: |
|
|
|
|
|
|
|
|
||||||||||
k = lim |
y |
= lim |
|
e x |
= |
+0 |
|
= +0 , |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x→−∞ x |
x→−∞ x2 |
|
+∞ |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
e x |
|
|
|
|
e x |
|
|
+0 |
|
|||
b = lim ( y − kx ) |
= lim |
|
− 0 x |
= |
lim |
|
= |
|
|
|
= −0 . |
|||||||
|
|
|
||||||||||||||||
x→−∞ |
|
|
|
|
|
|
|
|
|
x→−∞ x |
|
|
|
|||||
|
|
|
x→−∞ x |
|
|
|
|
|
−∞ |
|
||||||||
Коэффициенты k и b найдены, поэтому прямая y = kx + b = 0 x + 0 = 0 , т.е. y = 0 (ось Ox ) является левосторонней асимптотой (горизонтальной, частный
случай). Проведённое исследование знака числа b говорит о том, что график функции асимптотически приближается к оси Ox снизу.
4.5. Общая схема исследования функции и построения её графика.
Исследование функции и построение её графика рекомендуется проводить по следующей схеме.
1)Найти область определения функции.
2)Исследовать функцию на непрерывность. Найти точки разрыва функции и её односторонние пределы в этих точках.
3)Определить асимптоты графика и поведение функции на границе области определения.
4)Выяснить, является ли функция чётной, нечётной, периодической. При наличии какого–либо из этих свойств можно использовать симметрию при построении графика.
5)С помощью производной первого порядка найти промежутки возрастания и убывания, найти экстремумы функции.
6)С помощью производной второго порядка найти промежутки выпуклости и вогнутости графика функции, точки перегиба.
7)Используя результаты исследования, построить график функции. Построение графика удобно проводить в следующем порядке:
114

а) построить асимптоты; б) отметить точки экстремумов и точки перегиба;
в) соединить отмеченные точки в соответствии с поведением функции на интервале между ними.
При необходимости можно дополнительно найти значения функции в некоторых точках из тех промежутков, для которых предыдущие пункты исследования дали недостаточно информации. Их роль – проверка и уточнение построенного графика. Можно определить точки пересечения графика с осями координат, а также посмотреть, какой угол составляет касательная графика с осью Ox в некоторых точках графика и т. д.
Пример 5.8. Исследовать функцию f ( x ) = x3 и построить её график.
2( x + 1 )2
Решение. Следуем предложенной схеме исследования функции.
1)Функция определена при всех значениях x , кроме x = −1 .
2)Выясним характер разрыва функции при x = −1 . Для этого рассмотрим односторонние пределы функции в точке x = −1 :
lim |
x3 |
|
−1 |
|
, |
lim |
x3 |
|
−1 |
= −∞ . |
|||
|
= |
|
|
= −∞ |
|
= |
|
|
|||||
2( x + 1 )2 |
+0 |
2( x + 1 )2 |
+0 |
||||||||||
x→−1−0 |
|
|
|
|
x→−1+0 |
|
|
|
|||||
Полученные результаты говорят о том, что точка x = −1 является точкой разрыва 2-го рода для данной функции, а прямая с уравнением x = −1 – вертикальной асимптотой графика функции.
3) Ищем наклонные асимптоты:
k = |
|
lim |
f ( x ) |
|
lim |
|
x2 |
|
|
|
|
∞ |
|
lim |
|
|
2x |
|
|
∞ |
|
lim |
2 |
= 0,5 |
, |
|||||||||||||||
|
|
|
|
= |
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
= |
|
|
= |
|
||||||||||||||||
|
x |
2( x +1 )2 |
∞ |
4( x + 1 ) |
|
4 |
||||||||||||||||||||||||||||||||||
|
x→±∞ |
|
|
x→±∞ |
|
|
x→±∞ |
|
∞ |
|
x→±∞ |
|
|
|
|
|||||||||||||||||||||||||
b = lim ( f ( x ) − kx) = |
|
|
|
|
x |
3 |
|
|
|
|
|
x |
|
1 |
|
|
|
|
x |
3 |
− x( x + |
1 ) |
2 |
|
|
|||||||||||||||
lim |
|
|
|
|
− |
= |
|
lim |
|
|
|
= |
|
|||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||
|
|
x→±∞ |
|
|
|
|
|
|
|
|
|
2( x + |
1 ) |
|
|
2 |
|
2 x→±∞ |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
x→±∞ |
|
|
|
|
|
( x + 1 ) |
|
|
|
|
|
|||||||||||||||||||||
|
1 |
lim |
−2x2 |
− x |
|
∞ |
|
1 |
lim |
−4x −1 |
|
|
|
∞ |
|
|
1 |
lim |
|
−4 |
= −1 . |
|
|
|
|
|||||||||||||||
= |
|
|
|
|
|
|
= |
|
= |
|
|
|
|
|
|
|
= |
|
|
= |
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
2 x→±∞ ( x +1)2 |
|
∞ |
|
2 x→±∞ 2( x +1) |
|
|
|
∞ |
|
|
2 x→±∞ |
|
|
|
|
|
|
|||||||||||||||||||||
Обратим внимание на то, что полученные результаты одинаковы как при |
||||||||||||||||||||||||||||||||||||||||
x → +∞ , |
так и при x → −∞ . Из существования этих конечных пределов следует, |
|||||||||||||||||||||||||||||||||||||||
что график функции имеет двустороннюю наклонную асимптоту y = 0,5 x − 1 .
4) Чётной или нечётной функция f ( x ) не является, так как её область определения не симметрична относительно x = 0 (например, при x = 1 функция определена, а при x = −1 не определена).
Периодической функция тоже не является, так как среди элементарных функций периодическими могут быть только тригонометрические функции.
115

5) Вычислим производную 1-го порядка: |
|
|
|
|
|
|
|||||||||
|
x3 |
|
′ |
|
1 3x2 |
( x + 1 )2 − x3 2( x + 1 ) |
|
1 x2 ( x + 3 ) |
|
||||||
f ′( x ) = |
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
4 |
|
|
|
3 |
|
|||||
|
2( x + 1 ) |
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
( x + 1 ) |
|
|
( x + 1 ) |
|
|||||
Приравнивая f ′( x ) нулю, получим критические точки 1-го рода:
|
1 |
|
x2 ( x + 3 ) |
= 0 x2 ( x + 3 ) = 0 x1 = 0 , x2 = −3 . |
||||
2 |
|
|||||||
|
|
( x + 1 )3 |
||||||
|
|
|
|
|||||
|
|
|
|
|
||||
Знак |
f ′( x ) «+» −3 «−» −1 «+» 0 «+» x |
|||||||
Кроме того, |
f ′( x ) не существует при x = −1 . Отметим найденные точки на |
|||||||
оси и в каждом из четырёх полученных интервалов определим знак f ′( x ). Итак,
функция возрастает на интервалах ( −∞ ,−3 ) , ( −1 ,+∞ ) и убывает на интервале |
||||||
( −3;−1 ) . |
|
|
|
|
|
|
В точке x = −3 функция |
f ( x ) определена и производная f ′( x ) меняет знак |
|||||
с «+» на «–», поэтому |
x = −3 – точка максимума. Значение функции в этой точке |
|||||
f ( −3 ) = |
|
( −3 )3 |
|
= − |
27 |
≈ −3,4 . |
|
−3 + 1 )2 |
|
||||
2( |
8 |
|
||||
В точке x = −1 функция не определена и, хотя |
f ′( x ) меняет знак при перехо- |
|||||||||||||||||
де через эту точку, точка x = −1 не является точкой экстремума. |
|
|
|
|||||||||||||||
Точка x = 0 |
также не является точкой экстремума, так как f ′( x ) не меняет |
|||||||||||||||||
знак при её переходе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6) Вычислим производную 2-го порядка: |
|
|
|
|
|
|
||||||||||||
f ′′( x ) = |
1 |
x3 + 3x2 |
′ |
|
1 ( 3x2 + 6 x )( x + 1 )3 − x2 ( x + 3 ) |
3( x + 1 )2 |
||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
3 |
|
|
|
|
|
|
6 |
|
|
|
||||
|
2 |
|
( x + 1 ) |
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
( x + 1 ) |
|
|
|
|
|||||||
|
|
|
|
= |
1 |
|
|
3x ( |
( x + 2 )( x + 1 ) − x( x + 3 )) |
= |
3x |
|
. |
|
||||
|
|
|
|
2 |
|
|
|
|
|
( x + 1 )4 |
|
( x + 1 )4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Приравнивая |
f ′′( x ) нулю, получим критическую точку 2-го рода: x =0 . Кроме |
|||||||||||||||||
того, f ′′( x ) не существует при x = −1 . Отметим эти две точки на оси и определим знаки f ′′( x ) на полученных интервалах.
Итак, на интервале ( −∞, 0 ) график выпуклый, на интервале ( 0, + ∞ ) – вогну116
тый. При x = 0 график имеет перегиб. Так как |
f ( 0 ) = 0 , то точка O( 0;0 ) – |
|||||||||
точка перегиба. |
|
|
|
|
|
|
|
|
|
|
Знак f ′′( x ) «–» −1 |
«–» |
0 |
«+» |
x |
|
|
|
|||
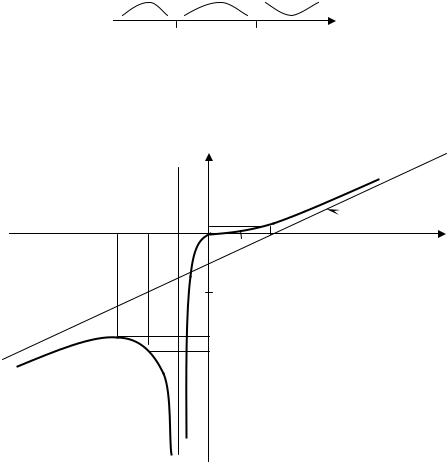
7) Используя полученные результаты, строим график функции (см. рисунок). |
||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
Для уточнения графика функции вычислены точки |
A( −2;−4 ) и B 2; |
|
|
этого |
||||||
|
||||||||||
графика. |
|
|
|
|
|
|
9 |
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
|
|
|
|
|
|
x = –1 |
|
1 |
B |
|
y = 0,5x–1 |
|
|
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
–3 –2 –1 |
|
|
О |
2 |
|
|
x |
|
||
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
–3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–3,4 |
|
|
|
|
|
|
A |
|
|
–4 |
|
|
|
|
|
|
|
5. Нахождение наибольшего и наименьшего значений функции
Многие практические задачи сводятся к отысканию наибольшего и наименьшего значений функции на каком либо множестве, т. е. значений функции больших (меньших) всех других её значений на этом множестве (а не только значений в близких точках, как это получается в точках локального экстремума).
Если функция задана и непрерывна на отрезке [a,b], то такие значения существуют. При этом наибольшим значением M и наименьшим значением m функции
117
y = f ( x ) может оказаться значение этой функции в одной из критических точек 1-го рода этого отрезка или значение функции на концах [a,b].
Правило отыскания наибольшего (наименьшего) значений функции на отрезке
[a,b]:
1)найти критические точки 1-го рода x = xi (a, b);
2)вычислить значения f(xi ), f(a), f(b);
3)выбрать из полученных чисел самое большое (малое), это и будет наиболь-
шее M (наименьшее m) значение функции. При этом будет ясно, при каком значении аргумента x [a, b] будет достигнуто M и m.
Пример 5.9. Найти наибольшее и наименьшее значения функции f(x) = 2x3 − 3x2 + 1 на отрезке [−1; 2].
Решение. Ищем критические точки 1-го рода заданной непрерывной функции: f ′( x ) = 6x2− 6x; f ′( x ) = 0 6x2− 6x = 0 x(x−1) = 0 x1 = 0, x2 = 1
– критические точки, обе внутри отрезка [−1; 2].
Вычислим значения функции в критических точках и на концах отрезка: f(−1) = − 4; f(0) = 1; f(1) = 0; f(2) = 5.
Так как самое большое из этих чисел равно 5, а самое малое равно (− 4), поэтому наибольшее значение M = f(2) = 5 (достигается при x = 2, т. е. на правом
конце отрезка), наименьшее значение m = f(− 1) = − 4 (достигается при x = − 1, т. е. на левом конце отрезка).
Замечания.
1. Если непрерывная функция f(x) на отрезке [a,b] возрастает (убывает), то m = f(a), M = f(b) (m = f(b), M = f(a)).
2. Пусть непрерывная функция f(x) на отрезке [a,b] имеет только один экстремум f(x0), x0 (a,b). Если в этой точке функция имеет максимум (минимум), то без сравнения с граничными значениями ясно, что M = f(x0) (m = f(x0)). Важно подчеркнуть, что сказанное справедливо и в случае, если функция задана на открытом промежутке (a,b), или на бесконечном промежутке.
К задачам рассмотренного типа приводятся многие практические задачи. Особенностью таких задач является то, что не задана функция, подлежащая исследованию. Поэтому вначале следует, исходя из условий задачи, выбрать независимую переменную и выразить исследуемую величину через эту переменную (т. е. задать функцию аналитически). При этом промежуток изменения независимой переменной, который может быть конечным или бесконечным (т. е. область определения функции), также следует определить из условия задачи.
118

Пример 5.10. Найти такой цилиндр, который имел бы наибольший объём при данной полной поверхности S.
Решение. Объём искомого цилиндра V примем за функцию. Объ`м цилиндра
зависит от двух величин – радиуса основания r и высоты h: V =πr 2h . Одну из этих переменных – радиус основания – примем за аргумент х. Тогда другую переменную h (высоту) – выразим через х и известную величину S (полную поверхность):
|
|
|
|
|
|
S = 2π x2 + 2π xh h = |
S − 2π x2 |
= |
S |
|
|
− x . |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2π x |
|
2π x |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
S |
|
|
|
|
|
S |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||
Составим функцию V = |
π x |
|
|
|
|
|
|
|
|
− x |
= |
|
|
x − |
π x |
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2π x |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Исследуем её на экстремум: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Vx′ = |
S |
−3π x2 ; Vx′ |
=0 |
|
S |
|
− 3π x2 =0 |
|
|
x = |
|
|
S |
|
|
– критическая точка. |
||||||||||||||||||||||||
|
2 |
|
6π |
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
′′ |
< 0 , то при x = |
|
S |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Найдём Vxx = −6π x . Так как при x = |
|
6π |
имеем Vxx |
|
6π |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
объём цилиндра будет наибольшим. При этом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
h = |
|
S |
|
|
6π |
− |
S |
|
= |
|
6π S 2 |
|
− |
|
S |
= |
|
6 S |
− |
|
|
|
S |
= |
2 |
S |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2π |
|
S |
6π |
|
|
4π |
2 S |
|
|
6π |
|
2 6π |
|
|
6π |
6π |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Получили, что 2 x = h , т. е. наибольший объ`м будет у цилиндра с квадратным осевым сечением.
Варианты заданий контрольной работы № 5
5.1. Вычислить пределы функций с помощью правила Лопиталя.
1. 1)
2. 1)
3. 1)
lim
x→0
lim
x→0
lim
x→0
3 1 −6 x −1 + 2 x |
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
2 |
|
1 |
|
|||||||||||||
; 2) |
lim |
− |
|
; |
|
3) |
lim |
(2 − 4sin |
x )ln cos x . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
sin |
2 |
x |
|
ln x |
|
|
||||||||||||||||||||||||
|
|
x→1 |
ln x |
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
||||||||||||
x arctgx |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
x−2 |
|
|||||||||
; |
|
|
2) |
lim |
− |
|
|
|
; |
3) |
lim |
(2e x −1) x . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
lncos x |
|
|
|
|
|
x→1 |
ln x |
|
|
x − 1 |
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|||||||
cos 3x −ex |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
(cos |
x )x . |
||||||||||||||||
|
|
|
|
|
|
; |
2) |
lim |
ctgx − |
|
|
; |
|
|
|
|
3) |
|||||||||||||
arctg |
2 |
5 x |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
x |
|
|
|
|
|
x→0+0 |
|
|
|
|
|
|
|
|
|||||||
119

4. 1) lim |
1 + x2 −cos 4 x |
; 2) lim |
ctg2 x |
; |
|
ln2 (1 + x) |
ln x |
||||
x→0 |
x→0 +0 |
|
5. 1)
6. 1)
7. 1)
8. 1)
9. 1)
10. 1)
11. 1)
lim |
e x − x −cos 2 x |
; |
|
|||||||||||||
|
|
sin(x |
2 |
) |
|
|
|
|
|
|||||||
x→0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
ln(1 − 3 x)+ 3 x |
|
; |
|||||||||||||
|
|
|
|
|
|
|
||||||||||
x→0 |
|
|
arcsin2 5 x |
|
|
|||||||||||
lim |
|
|
|
x |
2 |
|
|
|
|
|
; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x→0 e2 x − |
1 + 2 x |
|
|
|||||||||||||
lim |
|
3 |
1 +6 x −e |
2 x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||
|
|
|
sin2 |
2 x |
|
|
|
|
|
|||||||
x→0 |
|
|
|
|
|
|
|
|
|
|
||||||
lim |
e−x −cos 2 x |
; |
|
|
|
|
|
|||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||||
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
|
|
|
x2 |
|
|
|
|
|
|
|
; |
|||
|
|
|
|
|
|
|
|
−5 x |
||||||||
x→0 ln(1 + 5 x) |
|
|||||||||||||||
lim |
π − 2arctg2 x ; |
|
||||||||||||||
x→+∞ |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
e x |
− 1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
lim |
e2 x |
; |
|
|
|
|
|
|||
|
x4 |
|
|
|
|
|
|||||
|
x→+∞ |
|
|
|
|
|
|
|
|||
2) |
lim(π − 2 x )tg x ; |
||||||||||
|
x→π |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2) |
lim |
|
|
x ln x ; |
|
|
|
|
|
||
|
x→0 +0 |
|
|
|
|
|
|
|
|
||
2) |
lim |
|
|
ln tg x |
; |
|
|
|
|
||
|
ln tg 2 x |
|
|
|
|||||||
|
x→0+0 |
|
|
|
|
|
|
||||
2) |
lim |
x − arctg2 x |
|
; |
|
|
|||||
|
|
|
|||||||||
|
x→0 |
|
|
|
x 3 |
|
|
|
|
|
|
2) |
lim( 1 − x )tg |
π x |
; |
|
|||||||
|
x→1 |
|
|
|
|
2 |
|
|
|
|
|
2) |
lim |
|
|
ln( x − 4 ) |
|
|
; |
||||
|
|
ln( ex − e4 |
) |
||||||||
|
x→4+0 |
|
|
||||||||
|
|
|
1 |
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
||
3) |
lim |
x |
. |
|||||||
|
|
|
|
|||||||
1 + sin x |
||||||||||
|
x→0 |
|
|
|
||||||
|
|
|
5 |
|
|
|
|
|
||
3) |
lim (cos x) |
|
. |
|
||||||
tg2 5 x |
|
|||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
−2
3) lim (2 −cos x)x2 .
x→0
1
3) xlim→0 (cos(x2 ))sin4 x .
3) lim 5 −
x→0
3) lim (1 −
x→0
3) lim (1 +
x→0
4 ctg2 x |
. |
|
cos x
1
5 x)ln(1+2 x) .
−1
sin 2 x)tgx .
2
3) lim( ex + x )x .
x→0
12. 1) lim |
ex2 − 1 |
; |
|
cos x − 1 |
|||
x→0 |
|
|
|
|
|
|
|
1 |
|
− 2tgx |
|
|||
|
|
|
|
cos2 |
|
|
||||||
13. 1) |
lim |
x |
|
|
; |
|||||||
|
|
|
|
|
|
|||||||
|
π |
1 + cos 4 x |
|
|
|
|||||||
|
x→4 |
|
|
|
|
|
|
|
||||
14. 1) |
lim |
|
x cos x − sin x |
|
; |
|||||||
|
|
|
|
|||||||||
|
x→0 |
3 |
|
x3 |
|
|
|
|||||
|
|
|
|
1 + 2 x + 1 |
|
|
|
|||||
15. 1) |
lim |
|
|
|
|
|
; |
|
|
|||
|
2 + x + x |
|
|
|||||||||
|
x→−1 |
|
|
|
||||||||
16. 1) |
lim |
|
|
e x − 2x |
|
|
|
|||||
|
|
|
|
|
; |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
x→0 x |
1 − x2 |
|
|
|
|||||||
2) lim arcsin 2 x ctg x ; |
3) lim( 3 − 2 x )tg |
π |
x |
. |
|
2 |
|||
x→0 |
x→1 |
|
|
|
2) |
lim |
ln( x − 1 ) |
|
; |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x→1 |
ctgπ x |
|
|
|
|
|
|
|
|
|
||||||||||
2) |
lim |
|
|
|
|
ln x |
|
|
|
|
|
|
; |
||||||||
1 + 2 ln sin x |
|||||||||||||||||||||
|
x→0+0 |
|
|||||||||||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
2) |
lim |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
; |
|
||||
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
x→0 |
|
|
|
|
|
sin x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
e |
|
1 |
|
|
|
|
|
|
|
|
|
|||
2) |
lim |
|
|
|
1−x |
|
|
|
|
; |
|
|
|
||||||||
|
ln( 1 − x ) |
|
|
|
|||||||||||||||||
|
x→1−0 |
|
|
|
|
|
|||||||||||||||
3) |
lim(π − 2 x )cos x . |
||||
|
x→π |
||||
|
2 |
|
|
|
|
|
3 |
|
|
||
3) |
lim(cos 2 x ) |
x2 |
. |
||
|
x→0 |
||||
|
1 |
|
|
||
3) |
lim( x + 2x ) |
x |
. |
||
|
x→∞ |
||||
3) |
lim( tg2 x )sin x . |
||||
|
x→0 |
||||
120
