
zajcevVM
.pdf
5. Производная по направлению. Градиент
Производной функции z = f (x, y) в точке M ( x, y) в направлении вектора
uuuuuur |
∂z |
|
|
|
|
f (M1 ) − f |
(M ) |
|
|
|
|
|
|||||||||||
s = MM1 называется величина |
∂s |
= |
uuuuuurlim |
|
|
|
|
|
|
uuuuuur |
|
|
|
|
|
|
, которая показыва- |
||||||
|
|
MM1 |
|
→0 |
|
|
|
|
|
MM1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
||
ет скорость изменения функции z в точке M (x, y) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
в направлении вектора s . |
|||||||||||||||||||||||
Если функция z = f (x, y) дифференцируема, а cosα и cos β направляю- |
|||||||||||||||||||||||
щие косинусы вектора s , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z = |
∂z |
cosα + ∂z |
cos |
β . |
|
|
|
|
|
(6.5) |
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||
∂s |
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
s |
|
|
|
sy |
|
|
r |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Напомним, если s ={sx , sy } , то cosα = |
|
|
rx |
|
, |
cos β |
= |
|
|
r |
|
|
, |
s |
|
= sx2 + s2y . |
|||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
Для функции трех аргументов u = f |
(x, y,z) |
производная в направлении |
|||||||||||||||||||||
r |
|
|
|
|
|
cosα , cos β , cosγ |
|
равна |
|||||||||||||||
вектора s с направляющими косинусами |
|
|
|||||||||||||||||||||
∂∂us = ∂∂ux cosα + ∂∂uy cos β + ∂∂uz cosγ .
Градиентом функции z = f (x, y) в точке M (x, y) называется вектор, ко-
ординатами которого являются значения частных производных данной функции в точке M :
grad z (M ) = z′ |
(M ), z′ |
(M ) |
= z′ |
(M ) ir |
+ z′ |
(M ) rj . (6.6) |
{ x |
y |
} |
x |
|
y |
|
Направление градиента совпадает с направлением, вдоль которого функция изменяется быстрее всего, т. е. градиент функции указывает направление наибыстрейшего роста функции в точке M . Наибольшая скорость изменения функции z в
данной точке равна |
|
|
grad z (M ) |
|
: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
∂z (M ) |
|
grad z (M ) |
|
|
∂z (M ) 2 |
|
∂z (M ) |
2 |
|||||||
|
|
|
|
|
= |
= |
|
|
|
+ |
|
. |
||||
∂s |
|
|
∂x |
∂y |
||||||||||||
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
Пример 6.5. Вычислить производную функции z = x3y − 5xy2 + 1 в точке uuur
M(1; 1) по направлению вектора MN , где N – точка с координатами (0; 2). Най-
ти grad z (M ) и grad z (M ) .
131
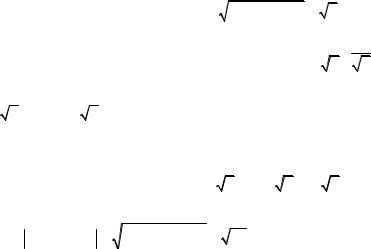
Решение. Имеем |
|
|
|
|
|
|||
uuur |
−1; 2 −1}={−1; 1}, |
uuuur |
= ( −1 )2 |
+( 1 )2 = 2 . |
||||
MN ={0 |
MN |
|||||||
|
|
|
|
uuur |
|
−1 |
|
|
|
вектор в данном направлении s = |
MN |
; |
|||||
Единичный |
uuuur |
= |
|
|||||
2 |
||||||||
|
|
|
|
MN |
|
|
||
|
|
|
|
|
|
|
|
|
, т. е.
2
cosα = − |
1 |
, cos β = |
1 |
. Найдём частные производные функции z в точке M: |
|
2 |
2 |
||||
|
|
|
z′x ( x, y ) = 3x2 y − 5 y2 z′x ( M ) = −2, z′y ( x, y ) = x3 − 10 xy z′y ( M ) = −9.
|
∂ z |
|
|
|
|
1 |
|
|
1 |
|
7 |
|
|
|
|
|
|
|
|||||||
По формуле (6.5) получим |
∂ s |
|
|
= −2 |
− |
|
|
− 9 |
|
= − |
|
. |
|
|
2 |
2 |
2 |
||||||||
|
|
M |
|
|
|
|
|
|
||||
|
|
|
|
|
|
Согласно (6.6) определяем grad z (M ) ={−2, −9} .
Поэтому grad z (M ) = (−2)2 +(−9)2 = 85 ≈ 9,2 . Это число равно наи-
большей скорости изменения данной функции z в точке M – скорости её изменения в направлении вектора grad z (M ) ={−2, −9} .
6. Экстремум функции
Функция u = f(M) в точке M0 имеет максимум (минимум), если в некоторой окрестности U( M0 ) этой точки значение f(M0) не меньше (не больше) значения функции в любой другой точке этой окрестности, т. е.
f(M0 ) ≥ f(M) ( f(M0 ) ≤ f(M) ) M U( M0 ) .
Максимум и минимум объединяются общим названием экстремум. Точку M0 называют в этом случае точкой экстремума.
Пусть функция u = f(M) имеет экстремум в точке M0 и дифференцируема в этой точке. Тогда все частные производные первого порядка в точке M0 обращают-
ся в нуль (необходимое условие экстремума).
Итак, точками экстремума дифференцируемой функции могут быть только те точки, в которых все частные производные первого порядка обращаются в нуль
(критические точки функции).
Удобным признаком наличия или отсутствия экстремума в критической точке для функции 2-х переменных является достаточный признак Сильвестра.
Пусть в критической точке M0(x0, y0) и некоторой её окрестности функция z = f(x, y) имеет непрерывные частные производные второго порядка. Вычислим
′′ |
|
′′ |
|
′′ |
|
|
|
A B |
2 |
( M0 |
( M0 |
( M0 |
) , |
D = |
|
= A C − B . |
|||
A = fxx |
), B = fxy |
), C = f yy |
B C |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
132 |
|
|
|
|
|

Тогда:
1)если D > 0, то в точке M0 функция f(M) имеем экстремум (максимум, если A < 0, минимум, если A > 0);
2)если D < 0, то в точке M0 функция f(M) не имеет экстремума.
Вслучае D = 0 экстремум в точке M0 может быть, а может не быть. Требуется дополнительное исследование.
Пример 6.6. Исследовать на экстремум функцию z = − 23 x3 + 2xy − y2 − 1 .
Решение. Находим частные производные z′x = −2x2 + 2 y, z′y = 2 x − 2 y . Приравнивая их нулю, составим систему и решим её:
|
−2 x2 + 2 y = 0 |
|
y |
= x |
2 |
x = 0 |
x = 1 |
. |
|||
|
2 x − 2 y = 0 |
|
|
= x |
|
= 0 |
или |
|
|||
|
|
|
y |
|
y |
y = 1 |
|
||||
Получили две критические точки M1(0; 0) и M2(1; 1). Вычислим частные |
|||||||||||
производные второго порядка: |
′′ |
= −4 x, |
′′ |
= 2, |
′′ |
= −2 . |
Так как |
||||
zxx |
zxy |
zyy |
|||||||||
A1 = z′′xx ( M1 ) =0, B1 = z′′xy ( M1 ) =2, C1 = z′′yy ( M1 ) =−2, D1 = A1C1 −B12 =−4 <0 ,
то в точке M1 экстремума нет.
В точке M2:
A2 = z′′xx ( M2 ) = −4, B2 = B1 = 2, C2 = C1 = −2, D2 = A2C2 − B22 = 4 > 0 .
Точка M2 – точка максимума, так как D2 > 0 и A2 < 0. Значение максимума f ( M2 ) = − 23 .
7. Наименьшее и наибольшее значения функции
Пусть функция z = f(x, y) определена и непрерывна в замкнутой области G с границей L на плоскости Oxy. Тогда она достигает наименьшее m и наибольшее M значения в этой области. Эти значения достигаются либо во внутренней точке (в этом случае это точка локального экстремума), либо на границе.
Правило нахождения наименьшего и наибольшего значений функции f(x, y) в
замкнутой области G нужно:
1)найти все её критические точки внутри области G;
2)вычислить значения функции в этих точках;
3)найти наименьшее и наибольшее значения функции на границе L области G;
4)из всех полученных значений выбрать наименьшее и наибольшее.
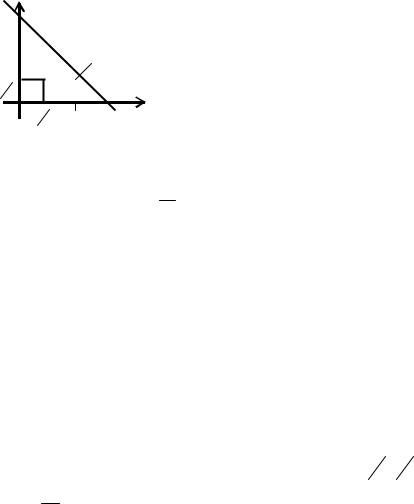
Пример 6.7. Найти наименьшее m и наибольшее M значения функции f(x, y) = xy(1 – x – y) в замкнутой области G, ограниченной линиями x = 0, x + y = 2, y = 0 (см. рисунок).
133
|
y |
|
|
|
|
2 |
A |
|
|
|
|
x=0 – |
G |
|
D |
x+y = 2 |
|
• M3 |
|
|
|
||
1 3 |
|
|
|
• |
B |
|
1 |
|
|
||
0 |
3 |
y=0 |
2 |
x |
|
|
|
|
|
|
|
Решение.
Ищем критические точки функции.
fx′ = y − 2xy − y2 , |
|
|
f y′ = x − x2 − 2xy . |
|||||
Решаем систему: |
|
|
||||||
f |
′ |
= y( 1 − 2 x − y ) = 0 |
|
|||||
|
x |
|
|
|
|
|
|
. |
|
|
= x( 1 |
− |
2 y − x ) = 0 |
||||
f y′ |
|
|||||||
|
|
|
|
|
|
|
|
|
Критические точки: |
O(0; 0), M1(0; 1), |
|||||||
M2(1; 0), M |
|
1 |
; |
1 |
|
|||
3 |
|
|
|
, из них только одна |
||||
3 |
3 |
|
||||||
|
|
|
|
|
|
|
||
критическая точка M3 внутри области G, остальные располагаются на границе данной области. Вычислим f ( M3 )= 271 .
Исследуем функцию на границе области.
1)На участке OB имеем y = 0 z ≡ 0.
2)На участке ОА имеем x = 0 z ≡ 0.
3) На участке АB имеем y = 2 – x, x [0; 2] z = x(2 – x)(1 – x – 2 + x) =
= x(x –2), x [0; 2]. Получили функцию z одной переменной x на промежутке [0; 2]. Её наименьшее и наибольшее значение достигается либо при x = 0, либо при x = 2, либо во внутренней критической точке:
dxdz = ( x2 − 2 x )′ = 2 x − 2 dxdz = 0 при x = 1.
Таким образом, нужно вычислить значения функции z в точках
O(0; 0), A(0; 2), B(2; 0), D(1; 1): z(O) = 0, z(A) = 0, z(B) = 0, z(D) = – 1.
Сравнивая найденные значения, приходим к выводу, что наименьшее значение функция принимает на границе области в точке D(1; 1): m = f (D) = −1 ;
наибольшее значение функция принимает внутри области в точке M3 ( 1 3 ; 1 3) :
M = f ( M3 ) = 271 .
8. Касательная плоскость и нормаль к поверхности
Касательная плоскость к поверхности в точке M0 есть плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.
Если поверхность задана уравнением F (x, y,z) = 0 , то уравнение касатель-
ной плоскости к ней в точке M0 (x0 , y0 ,z0 ) поверхности имеет вид:
134
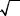
F ′ (M |
0 |
) (x − x |
) + F ′ (M |
0 |
) ( y − y |
) + F ′(M |
0 |
) (z − z |
) = 0 . (6.7) |
x |
0 |
y |
0 |
z |
0 |
|
Нормалью к поверхности называется прямая, перпендикулярная касательной плоскости в точке касания.
Канонические уравнения нормали к поверхности с уравнением F (x, y,z) = 0
в точке M0 (x0 , y0 ,z0 ) имеют вид: |
|
|
|
|
|
|
|
|
|
|
||||
|
x − x0 |
|
= |
|
y − y0 |
|
= |
z − z0 |
|
. |
(6.7) |
|||
|
|
) |
|
) |
|
) |
||||||||
|
F ′ (M |
0 |
|
|
F ′ (M |
0 |
|
F ′(M |
0 |
|
|
|||
|
x |
|
|
|
y |
|
|
z |
|
|
|
|||
Если же уравнение поверхности задано в виде |
z = f (x, y), |
то его можно |
||||||||||||
привести к виду F (x, y,z) = 0 : |
|
f (x, y)− z = 0 и пользоваться уже приведён- |
||||||||||||
ными формулами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 6.8. Найти уравнения касательной плоскости и нормали к эллиптиче-
скому параболоиду z = 2x2 + y2 в точке M0(1; −1; 3).
Решение. Запишем уравнение поверхности в виде 2x2 + y2 – z = 0.
Здесь x0 = 1, y0 = − 1, z0 = 3, F(x, y, z) = 2x2 + y2 – z.
Имеем F′( M |
0 |
) = 4 x |
= 4 , |
F′( M |
0 |
) = 2 y |
|
= −2 |
, F ′(M |
0 |
) = −1 . |
||||
x |
|
M0 |
y |
|
|
|
M0 |
|
z |
|
|||||
Итак, уравнение касательной плоскости: |
|
|
|
|
|
||||||||||
4(x − 1) + (−2)(y + 1)+(–1)(z − 3) = 0 или |
4x − 2y − z − 3 = 0. |
||||||||||||||
Уравнения нормали: |
|
x − 1 |
= |
y + 1 |
= |
z − 3 |
. |
|
|
|
|
|
|||
4 |
−2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
−1 |
|
|
|
|
|
||||
Варианты заданий контрольной работы № 6
6.1. Найти частные производные 1-го и 2-го порядка для функции z. Записать полный дифференциал.
1. |
z = ln(x − 2 y) . |
2. z = yx2 . |
|
4. |
z = y sin2 2x . |
5. |
z = xe− xy . |
7. |
z = x2 y . |
8. z = ln( x + ln y). |
|
10. |
z = x cos( x − 3 y) . |
11. |
z = yx y+1 . |
|
|
|
135 |
3. |
z = |
|
x2 |
|
. |
|
|
|||
1 |
− y |
|
|
|||||||
|
|
|
|
|
|
|||||
6. |
z = y ln |
x |
. |
|
|
|||||
|
|
|
||||||||
|
|
|
|
|
|
y |
|
|
|
|
9. |
z = ye2 y−x . |
|
||||||||
12. |
z = |
|
x2 |
− |
|
y |
|
. |
||
|
y2 |
|
x |
|||||||
|
|
|
|
|
|
|
||||
13. z = y ln( x − y ) . |
14. |
z = |
x2 − |
|
y . |
|
15. z = ln(e− y |
+ x) . |
|||||||||
16. z = |
|
1 − y2 |
. |
17. z = e− x2 y / x . |
|
18. z = yexy3 + x . |
|||||||||||
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
19. z = x cos2 (2 x − y). |
20. |
z = y2ex−3 y . |
|
|
21. z = |
x − y |
. |
|
|||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
22. z = ( 5 x − 1 )y2 x . |
23. |
z = |
|
|
y |
. |
|
24. z = y x − 4 y . |
|||||||||
|
x2 + 1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
25. z = x( y − 2 ln x) . |
26. z = |
y2 |
. |
|
|
|
27. z = x y1−x2 . |
||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
x |
|||
28. z = |
|
. |
29. |
z = y x |
|
+ 2 y |
. |
30. z = ln y − |
|
. |
|||||||
yex2 y |
|
y |
|||||||||||||||
6.2. Даны функция z = f (x, y), точка M0 , вектор s , замкнутая область G . |
|||||||||||||||||
Требуется найти: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) производную функции z = f (x, y) в точке M0 |
по направлению вектора s ; |
||||||||||||||||
2)градиент функции z = f (x, y) в точке M0 ;
3)величину наибольшей скорости изменения функции в точке M0 ;
4)наименьшее m и наибольшее M значения функции z = f (x, y) в областиG .
1. z = x2 − 4 xy − y2 + 2 y, M0 (2, 1) , sr ={3, 4} , G : x ≥ 0, 0 ≤ y ≤ 4 − x . 2. z = x3 − 3x2 + y2 − 2 y, M0 (1, 1), sr ={−5, 12} , G : x ≥ 0, x2 ≤ y ≤ 4 . 3. z = 2 x2 + xy − y2 + 9 y, M0 (1, 2), sr ={−3, 4} , G : x ≤ 2, 0 ≤ y ≤ 2 + x . 4. z = x2 − 2xy − y2 + 4 x, M0 (1, 1), sr ={3, −4} , G : x ≥ −3, 0 ≤ y ≤ −1 − x . 5. z = x2 − 4 xy − 2 y2 −6 x, M0 (1, 3) , sr ={5, 12} , G : x ≥ 0, 0 ≤ y ≤ 3 − x . 6. z = x2 − 2 xy + 4, M0 (−1, 2) , sr ={3, − 4} , G : 0 ≤ y ≤ 4 − x2 .
7. z = x2 + 2 xy − y2 − 4 x, M0 (1, −1) , sr ={6 , 8} , G : x ≤ 3, 0 ≤ y ≤ 1 + x . 8. z = 4 x2 + y2 + 2 y + 4 x, M0 (1, 0), sr ={−8, 6} , G : x ≤ 0, − 2 − x ≤ y ≤ 0 . 9. z = 5 x2 − 3xy + y2 −1, M0 (0, 2), sr ={3, 4} , G : x ≥ −1, −1 ≤ y ≤ 1 − x .
136
10. |
z = 4 x2 +9xy −4 x −6 y, M0 (0, 1), sr ={12, −5} , G : x ≥0, 0 ≤ y ≤ 1 − x . |
11. z = x2 + y2 −9xy + 27 , M0 (−1, 3), sr ={1, 1} , G : x + y ≤ 3, x ≥0, y ≥0 . |
|
12. |
z = 3 − 2x2 − y2 − xy, M0 (−1, 2), sr ={2, 2} , G : x ≤ 1, 0 ≤ y ≤ x . |
13. z = x2 + 3 y2 + x − y, M0 (−2, 1), sr ={4, 3} , G : x + y ≤ 1, x ≥ 1, y ≥ −1 .
14. |
z = x2 + 2 y2 + 2xy, M0 (−2, 0), sr ={3, 4} , G : −1 ≤ x ≤ 1, 0 ≤ y ≤ 2 . |
15. |
z =5 x2 −3xy + y2 +4, M0 (−1, 1), sr ={6, 8} , G : x + y ≤1, x ≥ −1, y ≥ −1 . |
16. z = 10 + 2xy − x2 , M0 (0, 1), sr ={8, −6} , G : 0 ≤ y ≤ 4 − x2 . |
|
17. |
z = x2 − y2 +2xy +4x, M (3, 1), sr ={5, 12} , G : x + y +2 ≥0, x ≤0, y ≤0 . |
|
0 |
18. |
z = x2 + xy − 2, M0 (−2, 1), sr ={−3, 4} , G : 4 x2 −4 ≤ y ≤ 0 . |
19. |
z = x2 + y2 − xy − x − y, M0 (2, 2), sr ={1, −1} , G : −1 ≤ x ≤ 1, 0 ≤ y ≤ 3 . |
20. z = x2 + y2 + xy, M0 (1, 0), sr ={−4, 3} , G : y − x ≤ 1, x ≤ 0, y ≥0 .
21. z = 3x2 − xy + x + y, M0 (1, −1), sr ={2, 2} , G : x − y ≤ 1, x ≥0, y ≤0 . 22. z = x2 + 3xy −6 y, M0 (2, 3), sr ={12, −5} , G : −1 ≤ x ≤ 1, 0 ≤ y ≤ 1 .
23. z = x2 − y2 +6 x + 3 y, M0 (1, 1), sr ={2, − 2} , G : x + y ≥ −1, x ≤0, y ≤0 .
24. |
z = x2 +3 y2 + 2xy, |
M0 (1, 2), |
sr ={4, −3} , G : x − y ≥ −1, 0 ≤ x ≤1, y ≥0 . |
25. z = x2 + y2 + 2x + y, M0 (2, 0), sr ={3, 4} , G : 0 ≤ x ≤ 2, 1 ≤ y ≤ 2 . |
|||
26. |
z = 3x2 + 2 y2 − xy, |
M0 (1, 3), |
sr ={6, −8} , G : −1 ≤ x ≤ 1, −1 ≤ y ≤0 . |
27. z = x2 − y2 +5 x + 4 y, M0 (1, 1), sr ={3, −4} , G : |
|
x |
|
≤ y ≤ 1 . |
|
|
|
||||
28. |
z = 2xy + 3 y2 −5 x, M0 (0, 1), sr ={3, 4} , G : 0 ≤ x ≤ 3, 0 ≤ y ≤ 1. |
||||
29. |
z = xy + 2 y2 − 2x +1, M0 (2, 0), sr ={8, −6} , G : x ≤ y ≤ 1, x ≥0 . |
||||
30. z = 2x2 + y2 + 3xy, M0 (2, 1), |
sr ={−4, 3} , G : x + y ≤ 2, x ≥ 0, y ≥ 1 . |
|
6.3. Исследовать на экстремум функцию z = f (x, y). |
||
1. |
z = y x − y2 − x +6 y . |
2. z = e0 ,5 x (x + y2 ) . |
3. |
z = x3 − y3 − 3xy . |
4. z = x3 + 8 y3 −6 xy + 1 . |
|
|
137 |

5. |
z = 2 x3 − xy2 + 5 x2 + y2 . |
6. z = x3 + 12 xy2 −15 x − 24 y . |
|||||||||||
|
|
1 |
|
|
1 |
|
|
|
2 |
|
|||
|
z = x2 + xy + y2 + |
+ |
|
|
8. z = 1 −(x2 + y2 ) |
|
. |
||||||
7. |
|
. |
3 |
||||||||||
|
|
|
|||||||||||
|
|
x |
y |
|
|
|
|
|
|
|
|||
9. |
z = x2 + y2 − xy + 9 x −6 y . |
10. z = x2 + xy + y2 − 2 x − y . |
|||||||||||
11. |
z = x3 + y2 −6 xy − 39 x + 18 y . |
12. z = xy + |
50 |
+ |
20 |
, ( x >0, y >0 ). |
|||||||
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
y |
||||
13. |
z = x2 + y2 − 2 ln x −18 ln y . |
14. z = 2 xy − 4 x − 2 y + 1 . |
|||||||||||
15. |
z = x3 + 3xy2 −15 x −12 y . |
16. z = 2 xy − 2 x −6 y −1 . |
|||||||||||
17. |
z = x4 + y4 − 2 x2 − 2 y2 + 4 xy . |
18. z = e x−y (x2 − 2 y2 ) . |
|||||||||||
19. |
z = x3 + y3 −15 xy . |
|
|
20. z = 3x2 − x3 + 3 y2 + 4 y . |
|||||||||
21. |
z = (x − y + 1)2 . |
|
|
22. z = 1 − x2 + y2 . |
|||||||||
23. |
z = x3 −6 x2 − 3 y2 + 9 x − 3 y . |
24. z = y3 − 3 y2 + 3x2 −9 y − x . |
|||||||||||
25. |
z = 9 x2 + 2 x3 + 2 y2 + 5 y − 24 x . 26. z = 3x2 + y3 +6 y2 + 9 y + x . |
||||||||||||
27. |
z = e2 x (x + y2 + 2 y) . |
|
|
28. z = xy (4 − x − y) . |
|||||||||
29. |
z = 4 (x − y)− x2 − y2 . |
|
|
30. z = x3 + y3 − 3xy . |
|||||||||
6.4. Составить уравнения касательной плоскости и нормали к поверхности, заданной уравнением, в указанной точке M.
1. |
z = x2 − y2 , |
M (5,4,3) . |
2. |
x + y + z = ez , |
M (2,−1,0). |
||||||
|
xyz = x + y +z , |
M (0,1,−1). |
|
z = arctg |
y |
|
|
|
|
π |
|
3. |
4. |
|
, |
M |
1,1, |
. |
|||||
x |
|||||||||||
|
|
|
|
|
|
|
|
|
4 |
||
5. |
z = x2 − 2 xy + y2 + y , M (1,1,1) . |
6. |
x2 + y2 −z2 =−1, M (2,2,3) . |
||
7. |
z = x2 + y2 −xy, |
M (1,1,1) . |
8. |
z3 − 3xyz = 2 , |
M (1,1,2) . |
9. |
x2 − y2 + z2 = 4 , |
M (2,1,1) . |
10. |
z2 = x2 + y2 , |
M (3,4,5) . |
11. z = yx2 , |
M (1,1,1) . |
12. |
xy = z2 − |
x |
+1 , |
M (1,1,1) . |
|
y |
|||||||
|
|
|
|
|
|
||
13. exz + e yz |
= 2 , M (1,1,0) . |
14. |
z = ( x − 5 y2 )2 , |
M (6 ,1,1). |
|||
|
|
138 |
|
|
|
|
|

15. xy + x2 + z3 + z = 11 , M (1,0,2) . |
16. y−2x +xyz =4, M (1,3,1). |
|||||||||||||
|
−z |
|
2 |
|
|
|
π |
|
π |
|
1 |
|
||
17. xyz=e |
+x −5, M (2,1,0) . |
18. |
z = sin x cos y , M |
|
, |
|
, |
|
. |
|||||
4 |
4 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
19. z = xy , |
|
M (1,1,1) . |
20. z = ye−x −2y2 + x2 , |
M (0,1,−1). |
||||||||||
21. z = x + y2 , M (1,2,5) . |
22. yz = xln( x2 + y2 ) +1 , M (0,1,1) . |
|||||||||||||
23. z = x32 + y32 , M (1,1,2) . |
24. x2 + 3z2 + xy − z = 2 , M (0,1,1) . |
|||||||||||||
25. |
ex z +ey z |
= 2e , M (1,1,1) . |
26. |
z2 + 2 y2 + 3 x = 4 , |
M (1,1,−1) . |
|||||||||
27. |
x2 − y2 + |
|
1 |
+ z = 2 , M (1,1,1) . |
28. |
z = ln( x2 + y2 ) + x2 , |
M (0,1,0) . |
|||||||
|
|
|||||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
||
29. |
ex z +ey z |
= 2e , M (1,1,1) . |
30. |
ex z +ey z = 2e , M (1,1,1) . |
|
|||||||||
139
