Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

book.pdf

Скачиваний:

281

Добавлен:

14.02.2015

Размер:

800.84 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2316 17 18 19 20 21 22 23 > Следующая >>>

Лекция 12. Введение в анализ

1. Числовая последовательность

Определение. Если каждому натуральному числу n поставлено в соответствие число xn , то говорят, что задана последовательность x1, x2 ,…, xn = { xn} .

Общий элемент последовательности является функцией от n xn = f (n) .

Таким образом последовательность может рассматриваться как функция порядкового номера элемента. Задать последовательность можно различными способами - главное, чтобы был указан способ получения любого члена последовательности.

Пример. {xn} = {(−1)n} или { xn} = −1;1; −1;1;…

{ xn} = {sin π n / 2} или { xn} = 1;0;1;0;…

Для последовательностей можно определить следующие операции: 1. Умножение последовательности на число m :

m{ xn} = {mxn} , т.е. mx1, mx2 ,…

2.Сложение (вычитание) последовательностей:

{xn} + { yn} = { xn + yn} .

3.Произведение последовательностей:

{xn} { yn} = { xn yn} .

4.Частное последовательностей:

{ x	}	x	n	при { yn} ≠ 0 .
n		=
{yn}
		yn

2. Ограниченные и неограниченные последовательности

Определение. Последовательность {xn} называется ограниченной, если существует такое число M > 0 , что для любого n верно неравенство: xn < M т.е. все члены последовательности принадлежат промежутку (−M ; M ) .

Определение. Последовательность {xn} называется ограниченной сверху, если для любого xn существует такое число M , что xn ≤ M .

Определение. Последовательность {xn} называется ограниченной снизу, если для любого n существует такое число M , что xn ≥ M .

Пример. {xn} = n - ограничена снизу {1, 2,3,…} .

Определение. Число называется пределом последовательности {xn } , если для любого положительного ε >0 существует такой номер N , что для всех n > N выполняется условие:

a − xn < ε

Это записывается: lim xn = a .

В этом случае говорят, что последовательность {xn } сходится к a при n → ∞ .

Свойство: Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

, т.к. n N , то

в самой точке

Пример. Доказать, что предел последовательности lim

(-1)n

= 0 .

Пусть при n > N верно

0 − (−1)n

< ε , т.е. 1

< ε . Это верно при n > 1 , таким образом, если

за N взять целую часть от 1 , то утверждение, приведенное выше, выполняется.

Теорема. Если xn

→ a , то

→

Доказательство. Из xn → a следует, что

xn − a

< ε . В то же время:

−

≤

xn − a

т.е.

−

< ε , т.е.

→

. Теорема доказана.

Теорема. Если xn

→ a , то последовательность {xn} ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности

последовательности не следует ее сходимость.

, при четном n

Например, последовательность xn =

не имеет предела, хотя

2 −

, при нечетном n

≤ 2

3. Монотонные последовательности

Определение.

1)Если xn+1 > xn для всех n , то последовательность возрастающая

2)Если xn+1 ≥ xn для всех n , то последовательность неубывающая.

3)Если xn+1 < xn для всех n , то последовательность убывающая

4)Если xn+1 ≤ xn для всех n , то последовательность не возрастающая

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Пример. Выяснить является возрастающей или убывающей последовательность {xn} =

Найдем x		= n + 1	. Найдем разность x	− x	=	n + 1	−	n	= n + 1− 5n	= 1− 4n
						5 5n		5n
n	+1	5n+1	n+1	n					5 5n	5 5n
1− 4n < 0 , т.е.	xn+1 < xn . Последовательность монотонно убывает.

nn . 5

4. Предел функции в точке

Пусть функция f (x) определена в некоторой окрестности точки x = a (т.е. x = a функция может быть и не определена).

Определение. Число A называется пределом функции f (x) при x → a , если для любого

ε > 0 существует такое число			> 0 , что для всех х таких, что 0<	x - a	<	верно неравенство
ε > 0 существует такое число			> 0 , что для всех х таких, что 0<	x - a	<	верно неравенство
	f(x) - A	<ε .
	f(x) - A	<ε .
	То же определение может быть записано в другом виде:
	Если а - <x<a + , x ≠ a,		то верно неравенство A-ε <f(x)<A+ε .

Запись предела функции в точке: lim f (x) = A.
x→a
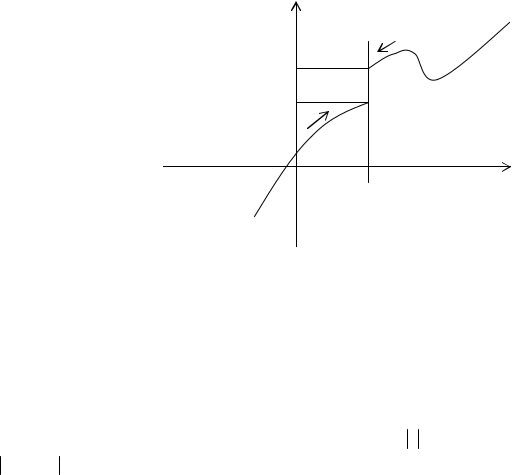
Определение. Если f (x) → A1 при x → a только при x < a , то lim		f (x) = A1 -
	x→a−0
называется пределом функции f (x) в точке x = a слева, a если	f (x) → A2	при x → a только
при x > a , то lim f (x) = A2 называется пределом функции f (x)	в точке x = a справа.
x→a−0

f(x)

Приведенное выше определение относится к случаю, когда функция f (x) не определена в самой точке x = a , но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы A1 и A2 называются также односторонними пределами функции f (x) в точке x = a . Также говорят, что A - конечный предел функции f(x) .

5.Предел функции при стремлении аргумента к бесконечности

Определение. Число A называется пределом функции f(x) при x → ∞ , если для любого

числа ε > 0 существует такое число M > 0 , что для всех x, x > M выполняется неравенство

A − f (x) < ε .

При этом предполагается, что функция f(x) определена в окрестности бесконечности. Записывают:

lim f (x) = A

x→∞

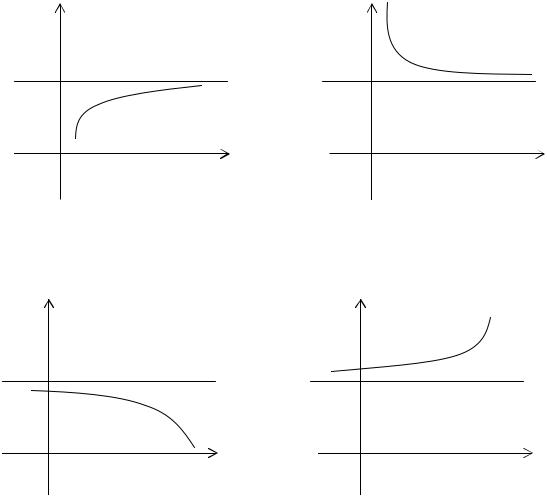
Графически можно представить:

Аналогично можно определить пределы lim f (x) = A для любого x > M и lim f (x) = A
для любого x < M .						x→+∞	x→−∞
для любого x < M .
6. Основные теоремы о пределах
Теорема 1 . lim C = C , где C = const .
x→a
Следующие теоремы справедливы при предположении, что функции f (x)							и g(x) имеют
конечные пределы при x → a .
Теорема 2 . lim( f (x) ± g(x)) = lim f (x) ± lim g(x)
x→a				x→a		x→a
Доказательство этой теоремы будет приведено ниже.
Теорема 3 . lim	[ f (x) g(x)]) = lim f (x) lim g(x)
x→a				x→a		x→a
Следствие. lim C f (x) = C lim f (x)
x→a				x→a
Теорема 4 . lim	f (x)	=	lim f (x)		при lim g(x) ≠ 0 .
	f (x)		x→a
	g(x)		lim g(x)
x→a	g(x)		lim g(x)			x→a
			x→a
Теорема 5 . Если f (x) > 0				вблизи точки x = a и lim f (x) = A, то A > 0 .
						x→a

Аналогично определяется знак предела при f (x) < 0, f (x) ≥ 0, f (x) ≤ 0 .

Теорема 6 . Если g(x) ≤ f (x) ≤ u(x) вблизи точки x = a и lim g(x) = lim u(x) = A , то и

x→a

lim = A .

x→a

Определение. Функция f (x) называется ограниченной вблизи точки x = a , если

существует такое число M > 0 , что

f (x)

< M вблизи точки x = a .

Теорема 7 . Если функция f (x) имеет конечный предел при x → a , то она ограничена

вблизи точки x = a .

Доказательство. Пусть lim f (x) = A, т.е.

f (x) − A

< ε , тогда

x→a

f (x)

f (x) − A + A

≤

f (x) − A

или

f (x)

< ε +

, т.е.

f (x)

< M , где M = ε +

Теорема доказана.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2316 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151.46 Mб80Belousov_N_A_Logika.pdf
#
03.05.2015810.58 Кб53Beusheva_fr1.pdf
#
25.09.20198.31 Mб7Blanki--INST_PRAKT.doc
#
18.09.2019498.69 Кб15Bogema.doc
#
14.02.2015149.5 Кб41Bonk_13-26.doc
#
14.02.2015800.84 Кб281book.pdf
#
14.02.2015192.51 Кб20Chernykh_A_G.doc
#
14.02.2015194.56 Кб30Chernykh_A_G.doc
#
14.02.20151.74 Mб32Chinkin-IR-OPD-Konspekt-lekcij.pdf
#
14.02.20152.81 Mб19cl-Ast-informatikaУЧЕБНОЕ ПОСОБИЕ.pdf
#
22.11.2019552.76 Кб3COLOURS (Автосохраненный).docx

Лекция 12. Введение в анализ

1. Числовая последовательность

2. Ограниченные и неограниченные последовательности

3. Монотонные последовательности

4. Предел функции в точке

5.Предел функции при стремлении аргумента к бесконечности

6. Основные теоремы о пределах