Кроме того, для точки М1 можно записать:
x − x1 |
= |
y − y1 |
= |
z − z1 |
. |
m |
n |
|
|||
|
|
p |
|||
Решая совместно эти уравнения, получим:
x − x1 |
= |
y − y1 |
= |
z − z1 |
. |
||||||
x |
|
− x |
y |
|
− y |
|
|||||
2 |
|
2 |
|
z |
2 |
− z |
|||||
|
1 |
|
|
1 |
|
|
1 |
|
|||
Это уравнение прямой, проходящей через две точки в пространстве.
13. Общие уравнения прямой в пространстве
Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей. Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:
N r + D = 0 , где
N - нормаль плоскости; r - радиусвектор произвольной точки плоскости.
Пусть в пространстве заданы две плоскости: N1 r + D1 = 0 и N2 r + D2 = 0 , векторы нормали имеют координаты: N1 (A1,B1,C1), N2 (A2,B2,C2); r (x,y,z).
Тогда общие уравнения прямой в векторной форме:
N |
1 |
r + D |
|
= 0 |
|
1 |
|
||
|
|
r + D |
|
= 0 |
N |
2 |
2 |
||
|
|
|
||
Общие уравнения прямой в координатной форме:
A1 x + B1 y + C1 z + D1 = 0A2 x + B2 y + C2 z + D2 = 0
Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.
Для этого надо найти произвольную точку прямой и числа m, n, p.
При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.
|
|
|
|
|
i |
j |
k |
|
B1 |
C1 |
|
A1 |
C1 |
|
A1 |
B1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
S = N |
1 |
× N |
2 |
= |
A B |
C |
= i |
− j |
+ k |
= i m + jn + kp. |
|||||||
|
|
|
1 |
1 |
1 |
|
B2 |
C2 |
|
A2 |
C2 |
|
A2 |
B2 |
|
||
|
|
|
|
|
A2 |
B2 |
C2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Найти каноническое уравнение, если прямая задана в виде:
2x − y + 3z − 1 = 05x + 4y − z − 7 = 0
Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.
y = 3z − 1 |
y = 3z − 1 |
y = 3z − 1 y = 2 |
, т.е. А(0,2,1). |
|
4y − z − 7 = 0 |
12z − 4 − z − 7 = 0 |
z = 1 |
z = 1 |
|
Находим компоненты направляющего вектора прямой.
39
m = |
|
B1 |
C1 |
|
= |
|
− 1 |
3 |
|
= −11; |
n = − |
|
A1 |
|
C1 |
|
|
= − |
|
2 |
3 |
|
= 17; |
p = |
|
A1 |
B1 |
|
= |
|
2 |
− 1 |
|
= 13. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
B |
2 |
C |
2 |
|
|
|
4 |
− 1 |
|
|
|
|
|
|
A C |
2 |
|
|
|
|
|
5 |
− 1 |
|
|
|
|
A B |
2 |
|
|
|
5 |
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
Тогда канонические уравнения прямой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
x |
|
= |
y − 2 |
= |
z − 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
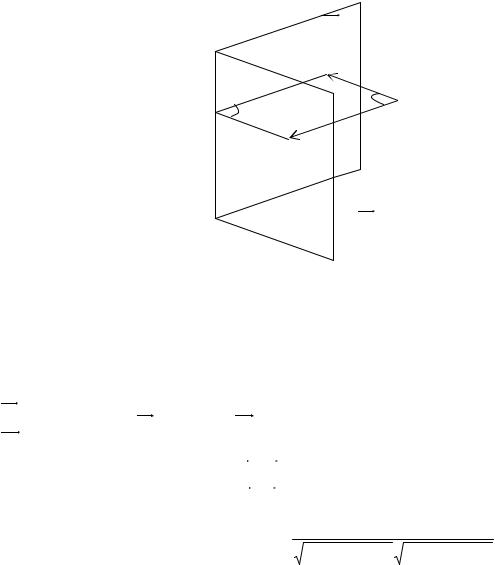
14. Угол между плоскостями
N2
ϕ1
N1
Угол между двумя плоскостями в пространстве ϕ связан с углом между нормалями к этим
плоскостям ϕ1 соотношением: ϕ = ϕ1 или ϕ = 180 − ϕ1 , т.е. |
|||||||
|
|
|
|
|
|
|
cosϕ = ± cosϕ1 . |
|
|
Определим угол ϕ 1 . Известно, что плоскости могут быть заданы соотношениями: |
|||||
N |
1 |
r + D |
|
= 0 |
|
|
|
|
1 |
|
, где N1 |
(A1,B1,C1), N2 |
(A2,B2,C2). Угол между векторами нормали найдем из их |
||
|
|
r + D |
|
= 0 |
|||
N |
2 |
2 |
|
|
|
||
|
|
|
|
|
|
||
скалярного произведения: cosϕ1 |
= |
|
|
N1 |
N2 |
. Таким образом, угол между плоскостями находится |
|||||||||
|
|
N1 |
|
N2 |
|
|
|||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
по формуле: cosϕ = ± |
A1 A2 + B1 B2 + C1C2 |
|
|||||||||||||
+ B2 |
+ C 2 |
A2 |
+ B2 |
+ C 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
A2 |
||||||
|
1 |
1 |
1 |
2 |
2 |
2 |
|||||||||
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
15. Условия параллельности и перпендикулярности плоскостей
На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:
A1 A2 + B1 B2 + C1C2 = 0 .
40
Параллельны, векторы нормалей коллинеарны: N1 N1 .Это условие выполняется
Плоскости, если: A1 = B1 = C1 .
A2 B2 C2
16. Угол между прямыми в пространстве
Пусть в пространстве заданы две прямые. Их параметрические уравнения: l1: r = r1 + S1t
l2: r = r2 + S2t
r = (x, y, z); r1 = (x1 , y1 , z1 ); r2 = (x2 , y2 , z2 ); S1 = (m1 , n1 , p1 ); S2 = (m2 , n2 , p2 ).
Угол между прямыми ϕ и угол между направляющими векторами ϕ этих прямых связаны соотношением: ϕ = ϕ1 или ϕ = 180 − ϕ1 . Угол между направляющими векторами находится из
скалярного произведения. Таким образом:
cosϕ = ± |
S1 |
S2 = ± |
|
m1m2 |
+ n1n2 + p1 p2 |
|
|||||
|
S |
1 |
S |
2 |
m2 |
+ n2 |
+ p2 |
m2 |
+ n2 |
+ p2 |
|
|
|
|
1 |
1 |
|
1 |
2 |
2 |
2 |
||
17. Условия параллельности и перпендикулярности прямых в пространстве
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были
пропорциональны. m1 = n1 = p1 m2 n2 p2
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю. m1m2 + n1n2 + p1 p2 = 0
18. Угол между прямой и плоскостью
Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.
α |
N |
S |
|
|
α
Пусть плоскость задана уравнением N r + D = 0 , а прямая - r = r0 + St . Из геометрических соображений (см. рис.) видно, что искомый угол α = 900 − ϕ , где α - угол между векторами N и S . Этот угол может быть найден по формуле:
41
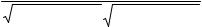
cosα = |
|
N S |
|
sinϕ = ± cosα = ± |
|
|
N S |
. |
||||||||||
|
N |
|
S |
|
|
|
N |
|
|
|
S |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В координатной форме: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
sinϕ = ± |
Am + Bn + Cp |
|||||||||||||||||
+ B2 + C 2 m2 + n2 + p2 |
||||||||||||||||||
|
|
|
|
A2 |
||||||||||||||
19. Условия параллельности и перпендикулярности прямой и плоскости в пространстве
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
N S, N S = 0, sinϕ = 0, |
Am + Bn + Cp = 0. |
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарны. Это условие выполняется, если векторное произведение этих векторов было равно нулю.
N × S = 0; |
A |
= |
B |
= |
C |
|
m |
n |
p |
||||
|
|
|
42