10. Наибольшее и наименьшее значение функции

Согласно теореме Вейерштрасса, если функция непрерывна наотрезке , то она принимает на нем наибольшего и наименьшего значения. Наибольшее и наименьшее значения функции может достигаться как в точках экстремума, так и в точках на концах отрезка.

Для отыскания наибольшего и наименьшего значений функции на отрезке рекомендуется пользоваться следующей схемой.

1. Находим производную .

2. Определяем критические точки функции, в которых или не существует.

3. Находим значения функции в критических точках и на концах отрезка и выбираем из них наибольшее и наименьшее.

Замечание. Если функция непрерывна наинтервале , то она может не принимать на нем наибольшего и наименьшего значения.

Если илибольше большего из значений функции в критических точках интервала, то наибольшего значения на всем интервале не существует. Аналогично не существует наименьшего значения, еслиилименьше меньшего из значений в критических точках.

Пример 1. Найти наибольшее и наименьшее значения функции на отрезке.

Решение:

1. Производная функции:

.

2. Приравниваем производную функцию к нулю 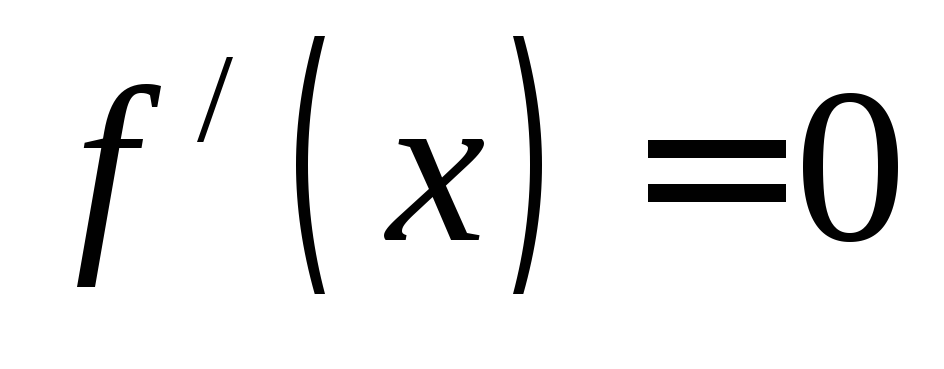и находим критические точки.

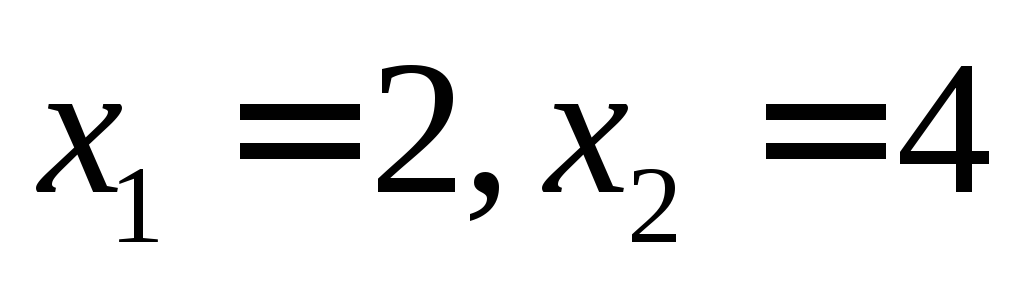3. Значения функции в критических точках 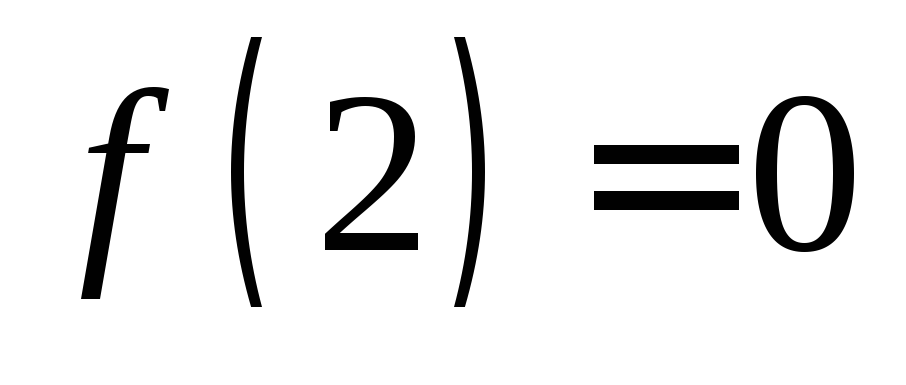,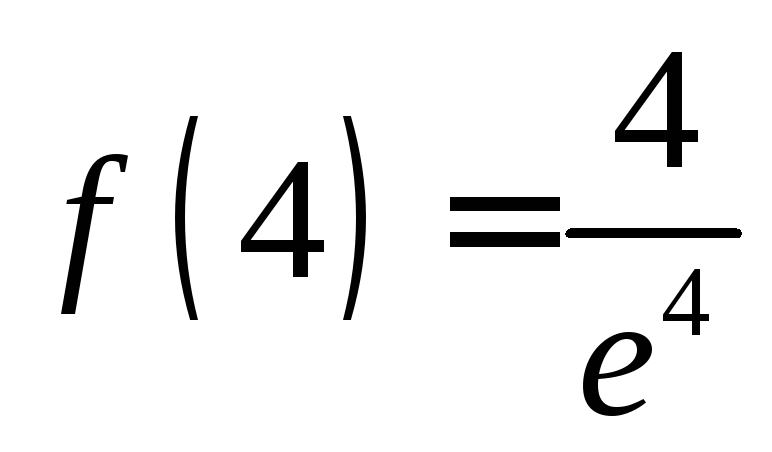и на концах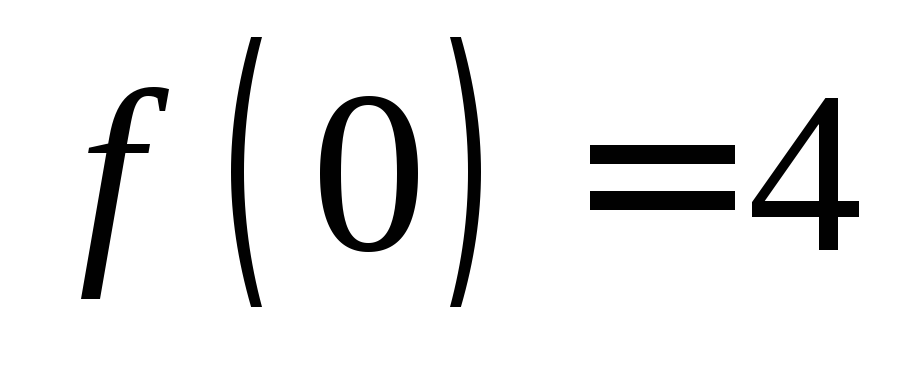и.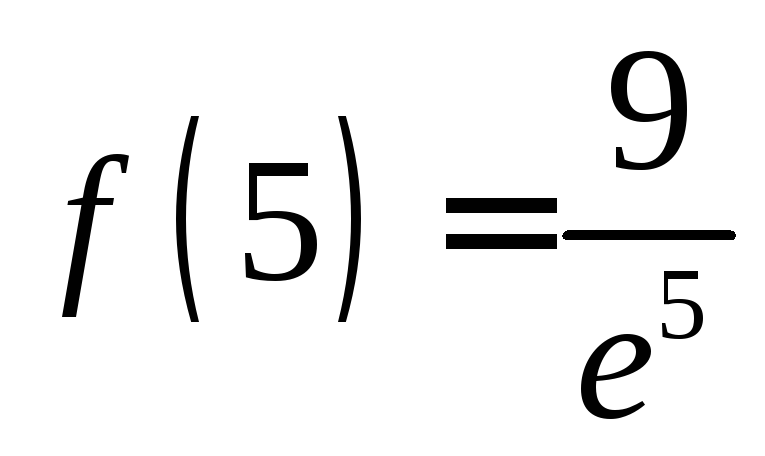

Следовательно, ,.

Пример 2. Найти наибольшее и наименьшее значения функции .

Решение: Функция определена на всей числовой оси. Изменение аргументане ограничено каким-либо отрезком. Поэтому исследуем функцию для. Вычисляем производную. Приравнивая производную к нулю, находим критическую точку:. При переходе через эту точку производная функции меняет знак с плюса на минус, следовательно,точка максимума. Если, функция бесконечно убывает, но наименьшего значения не имеет.

Пример 3. Найти наибольшее и наименьшее значения функции .

Решение: Функция определена на всей числовой оси. Изменение аргументане ограничено каким-либо отрезком. Поэтому исследуем функцию для.

Находим производную и приравниваем ее к нулю. Откуда,,,,. Подставляя найденные критические точки в функцию, находим, что при,функция имеет наибольшие значения, равные единице, а при,- наименьшие значения, равные.

Пример 4. Найти наибольшее и наименьшее значения функции .

Решение: Функция определена на всей числовой оси. Изменение аргументане ограничено каким-либо отрезком. Поэтому исследуем функцию для. Найдем производную. В точкепроизводная не существует. Значение функции приравно -1. Прифункция неограниченно возрастает. Следовательно, наименьшее значение функции будет, а наибольшего значения функция не имеет.

Найти наибольшее и наименьшее значения функции:

1. . Ответ: 9; -7.

2. .

Ответ: Наибольшее значение не существует; 64.

3. . Ответ:.

4. . Ответ: 1;.

5. . Ответ: 0,.

6. . Ответ:.

7. . Ответ:.

8. ,. Ответ:.

9. . Ответ:.

10. . Ответ:.

11. . Ответ:.

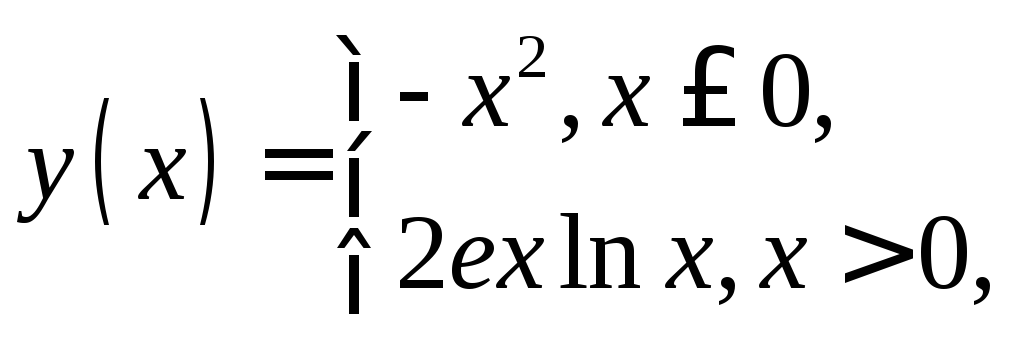
12. . Ответ:.

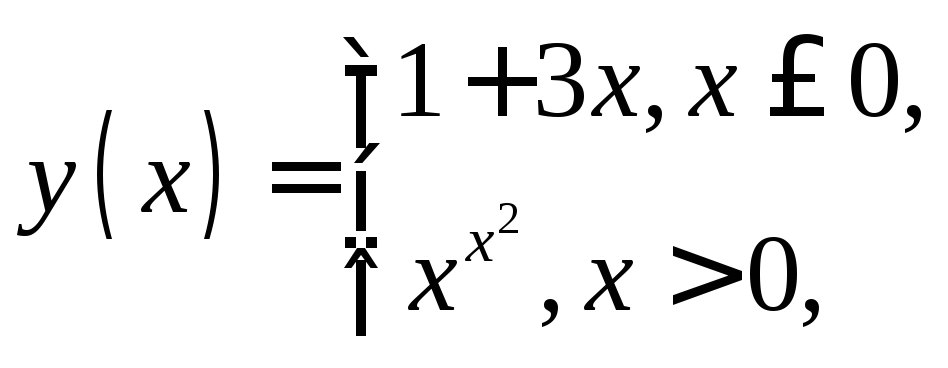
13. . Ответ:.