Самостоятельная работа
Найти пределы:
1.
.
Ответ:
.
2.
.
Ответ:
.
3.
.
Ответ:
.
4.
.
Ответ:
.
5.
.
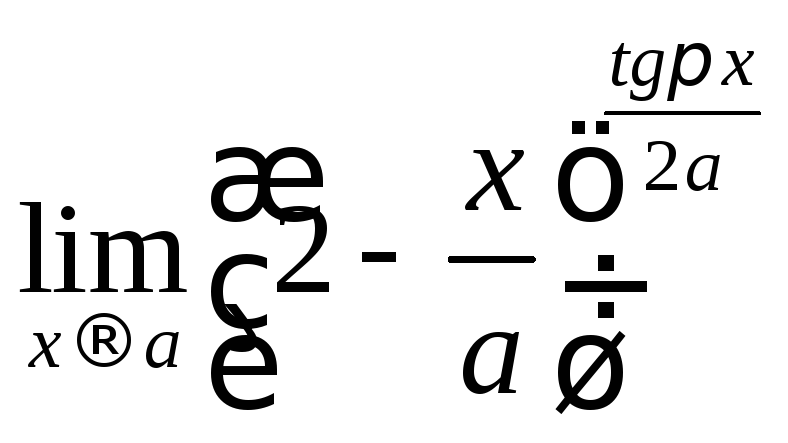Ответ:
.
6.
.
Ответ: 1.
7.
.
Ответ:
.
8.
.
Ответ:
.
9.
.
Ответ:
.
10.
.
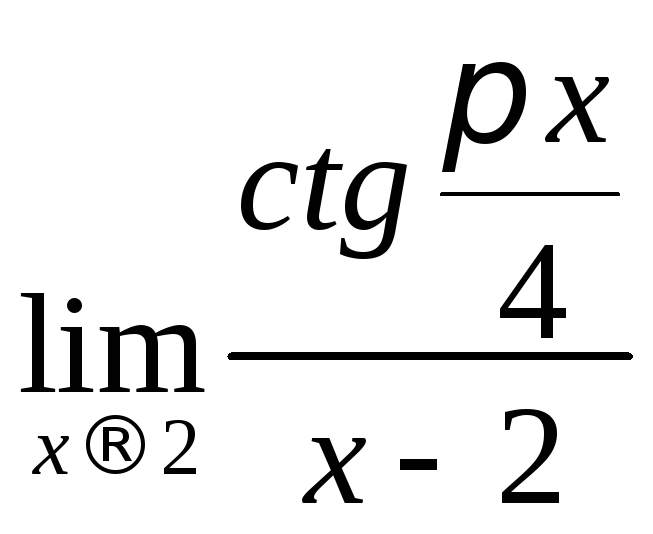Ответ:
.
11.
.
Ответ: 1.
12.
.
Ответ: 3.
13.
.
Ответ:
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
Примерный вариант контрольной работы
1.
Найти
:
a)
,
b)
,
c)
,
d)
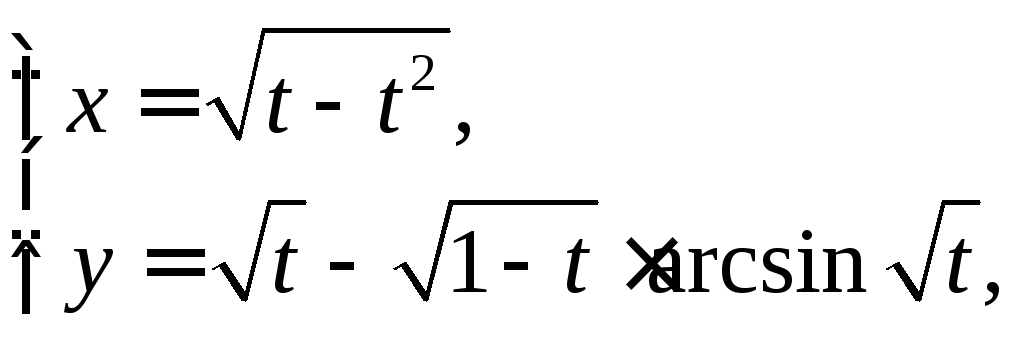e)
.
2.
Найти
:a)
,b)
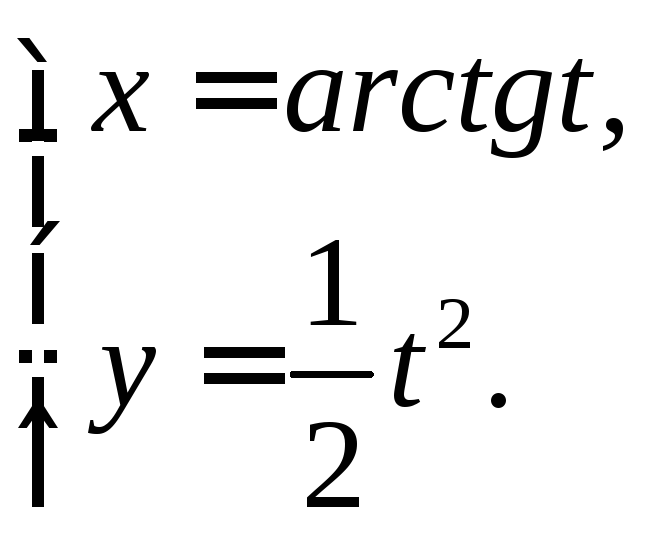
3. Составить уравнения касательных и нормалей в указанных точках к следующим кривым:
a)
,
,b)
.
4.
Вычислить приближенно с помощью
дифференциала значение функции
при заданном значении
:
,
.
5.
Вычислить
с помощью правила Лопиталя.
8. Возрастание и убывание функций
Возрастание
и убывание функции характеризуется
знаком ее производной. Если внутри
некоторого промежутка
,
то функция возрастает. Если
,
то в этом промежутке функция убывает.
При практическом исследовании функции на возрастание и убывание находят точки, в которых производная равна нулю или не существует. Все эти точки вместе с возможными точками разрыва функции разбивают область существования функции на ряд промежутков, на каждом из которых вопрос о возрастании или убывании функции определяется знаком производной.
Определить промежутки монотонности функций:
Пример
1.
.
Решение:
Функция определена для всех значений
.
Производная
при любом
.
Следовательно, функция возрастает на
всей числовой оси.
Пример
2.
.
Решение:
Функция существует для всех
.
Производная
.
Если
,
то
и
для всех
.
Следовательно, функция убывает
.
Пример
3.
.
Решение:
Функция определена для всех
.
В точке
она
терпит разрыв. Находим производную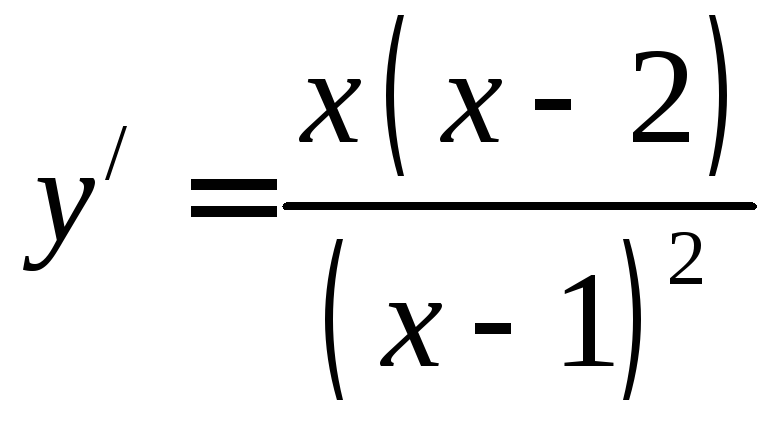
и приравниваем ее к нулю:
.
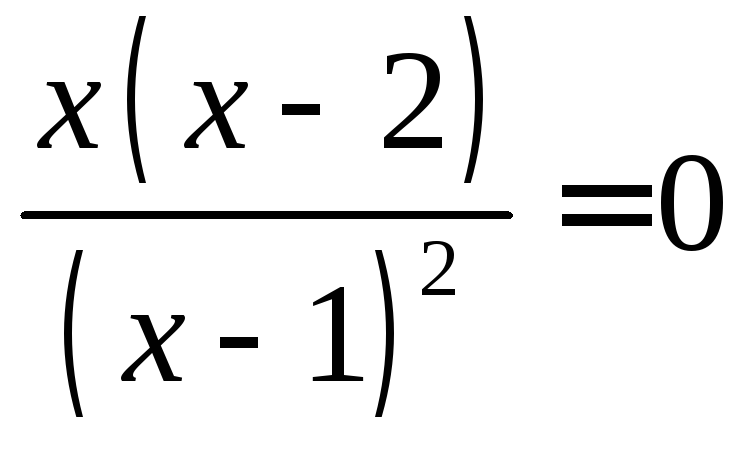Это уравнение имеет два корня:
.
Учитывая точку разрыва
,
разбиваем числовую ось на промежутки
и определяем знак производной на каждом
из них.
+ - - +
.
Следовательно,
функция возрастает на промежутках
и убывает -
.
Пример
4.
.
Решение:
Функция определена на всей числовой
оси. Находим нули производной:
и определяем промежутки и знаки функции
в каждом из них:
.
- - +
.
При
переходе через корень
производная не меняет знака. Если
и
,
,
и функция убывает. Если
,
производная
,
и функция возрастает.
Пример
5.
.
Решение:
Функция определена на всей числовой
оси. Находим ее производную:
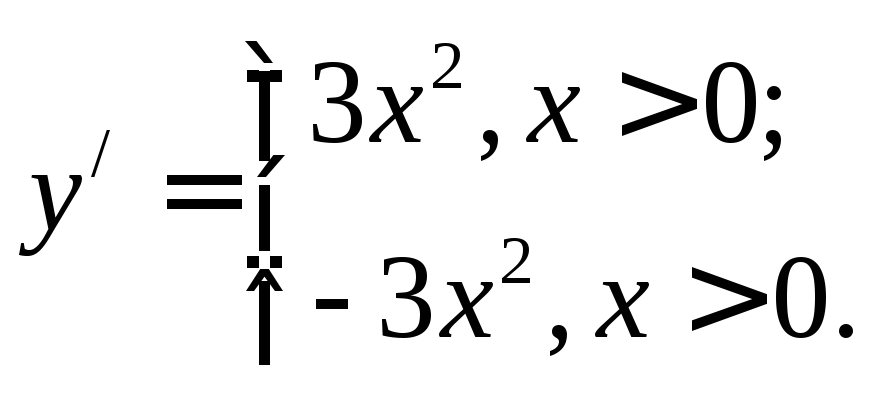Отсюда следует, что если
,
функция убывает, если
,
функция возрастает.
Найти интервалы возрастания и убывания функции:
1.
.
Ответ:
- интервалы возрастания,
-
интервалы убывания.
2.
.
Ответ:
- интервалы возрастания,
-
интервалы убывания.
3.
.
Ответ:
интервалы возрастания,
-
интервалы убывания.
4.
.
Ответ:
- интервал возрастания,
-
интервал убывания.
5.
.
Ответ:
- интервалы возрастания,
-
интервалы убывания.
6.
.
Ответ:
- интервал убывания.
7.
.
Ответ:
- интервалы убывания.
8.
.
Ответ:
- интервалы возрастания,
-
интервалы убывания.
9.
.
Ответ:
- интервалы возрастания,
-
интервалы убывания.
10.
.
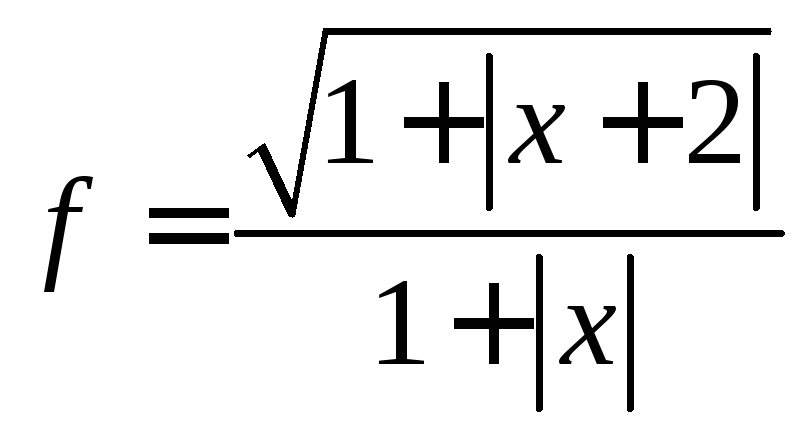Ответ:
- интервал возрастания,
-
интервалы убывания.
11.
Функция
задана неявно:
.
Ответ:
- интервал возрастания,
- интервал убывания.
12.
Функция
задана неявно:
.
Ответ:
- интервал возрастания,
- интервал убывания.
13.
Функция
задана параметрически: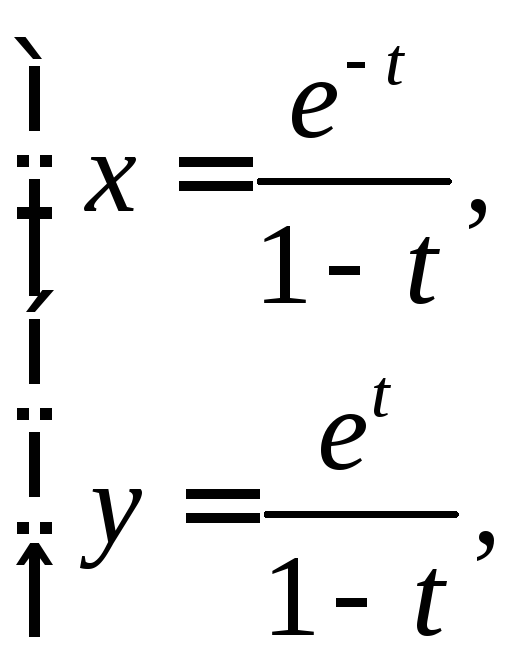
.
Ответ:
- интервал возрастания,
-
интервал убывания.
Выяснить,
при каких значениях параметра
функция
возрастает на всей числовой оси:
14.
.
Ответ:
.
15.
.
Ответ:
.
16.
.
Ответ:
.
17.
.
Ответ:
.
18.
.
Ответ:
.
19.
.
Ответ:
.