14. Исследование функции и построение графиков

При исследовании функций и построения их графиков рекомендуется использовать следующую схему.

1. Найти область определения функции.

2. Найти точки пересечения с осями координат, если они существуют. Найти интервалы знакопостоянства функции.

3. Проверить, является ли функция четной, нечетной, периодической. График четной функции симметричен относительно оси ОУ. График нечетной функции симметричен относительно начала координат.

4. Исследовать функцию на непрерывность. Найти точки разрыва и односторонние пределы в точках разрыва. Определить характер разрыва в окрестности точек разрыва. Найти вертикальные, горизонтальные, наклонные асимптоты графика, если они существуют.

5. С помощью производной первого порядка найти промежутки возрастания и убывания, найти экстремумы.

6. С помощью производной второго порядка найти промежутки выпуклости и вогнутости, точки перегиба.

7. Используя полученную информацию, построить график.

Пример 1. Исследовать функцию 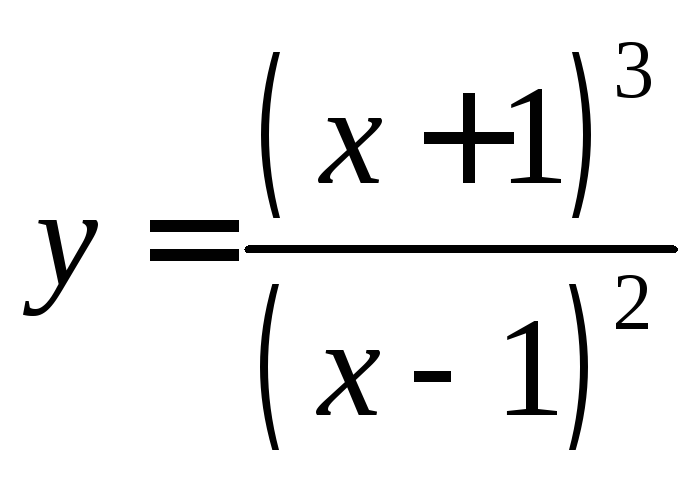и построить ее график.

Решение: Область определения .

Функция не является ни четной, ни нечетной, т.к. 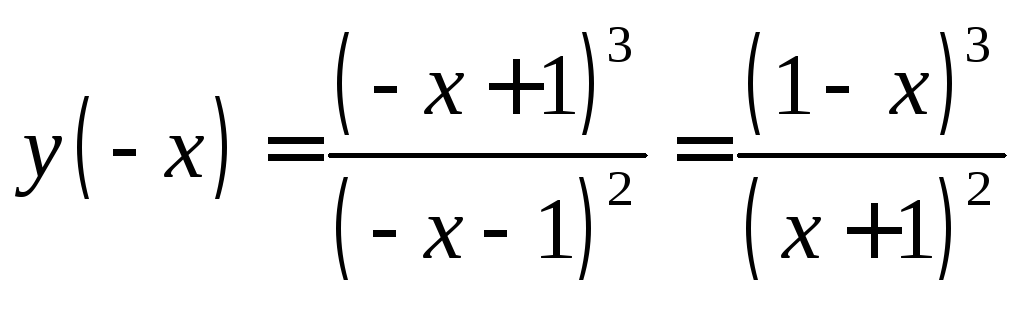. Функция не периодическая.

Нули функции: .

Отметим интервалы знакопостоянства функции на числовой оси. На оси обязательно надо нанести точку , в которой функция не определена. Знак функциизависит от знака числителя, т.к. знаменательпри всех:

- + + +

.

Выясним тип разрыва в точке . Для этого найдем пределы функции слева и справа в этой точке.

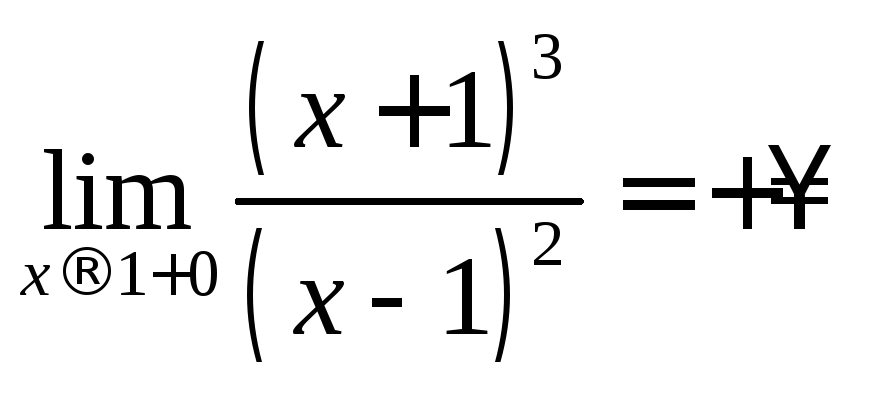, . Значит, точка- есть точка разрыва второго рода. Прямая- вертикальная асимптота графика функции.

Найдем наклонные асимптоты:

,

.

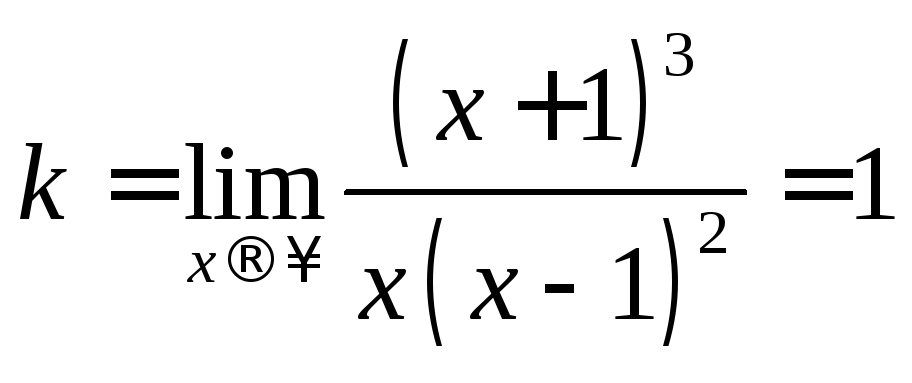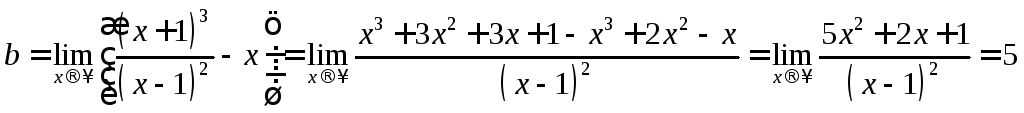Прямая - наклонная асимптота.

Найдем производную функции:

.

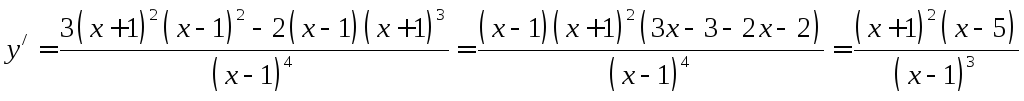Найдем критические точки первого рода – точки, в которых первая производная равна нулю или не существует:

при , т.е.;

не существует в точке .

Исследуем знак в окрестностях этих точек:

+ + - +

.

Функция возрастает на промежутках ;

Функция убывает на интервале .

Точка - есть точка минимума функции, точкане является точкой экстремума, т.к. функция в этой точке не определена.

Найдем вторую производную функции:

.

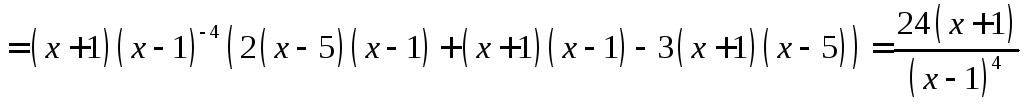Найдем критические точки второго рода:

при , т.е.;

не существует в точке .

Исследуем знак в окрестностях точек.

- + +

.

Точка - есть точка перегиба.

На интервале график функции выпуклый.

На промежутке график функции вогнутый.

Пример 2. Исследовать функцию и построить ее график.

Решение: Функция определена на всей числовой оси.

Функция общего вида, т.к. . Функция не имеет точек разрыва, значит, не имеет точек вертикальных асимптот.

Точка пересечения с осями координат одна .

Найдем наклонные асимптоты.

Вычислим .

.

Применяя правило Лопиталя .

Только для функция имеет горизонтальную асимптоту.

Первая производная определена на всей числовой оси, т.е. крититческими точками первого рода могут быть только нули производной:,.

Исследуем знак производной в окрестности точки :

+ -

.

Функция возрастает на интервале ; убывает на интервале. При переходе через точкупроизводная меняет знак с плюса на минус. Значит, точкаявляется точкой максимума..

Вторая производная определена на всей числовой оси, т.е. точки перегиба могут быть только там, где

: . На интервале, значит, график функции выпуклый; на интервале, значит, график функции вогнутый. Точкаявляется точкой перегиба функции.

Пример 3. Исследовать функцию 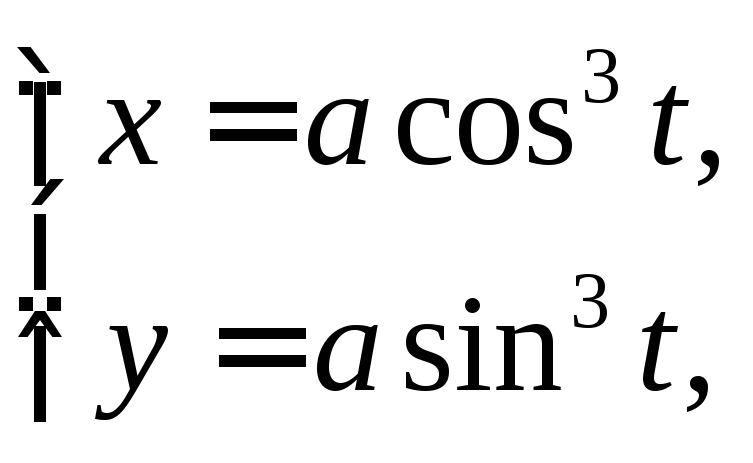и построить ее график. Решение: Функции определены для любого значения. Поскольку функциячетная, а функциянечетная, то график функции симметричен относительно оси ординат и начала координат, т.е. относительно координатных осей.

Полагая , находим, чтои. При таких значенияхиз выражениянаходим, что.

Полагая , находим, чтои. При этих значенияхиз выражениянаходим, что. Таким образом, график функции пересекает координатные оси в точках.

Найдем производные ,,,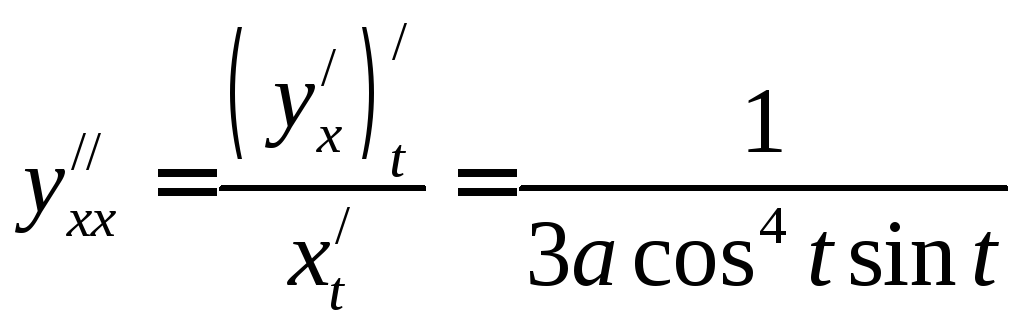. Из выражения для производнойопределяем критические точки. При,производная равна нулю, а при,не существует. Таким образом, область изменения параметраразбивается на четыре интервала.

При производная, т.е. функция убывает и график функции вогнутый. При, т.е. функция возрастает и график вогнутый. При, т.е. функция убывает и график выпуклый. При, т.е. функция возрастает и график выпуклый. Пользуясь симметрией графика функции, этот анализ можно было ограничить изменением параметра только одним интервалом, например..

При производнаяи касательные совпадают с осью, т.е. точкибудут точками возврата. Припроизводнаяне существует, а при, касательные совпадают с осьюи точкибудут также точками возврата. Полученная кривая представляет собой траекторию движения точки подвижного круга, катящегося изнутри по неподвижному кругу радиуса, и называетсяастроидой.

Исследовать функции и построить их графики:

1. .

2. .

3. .

4. .

5. .

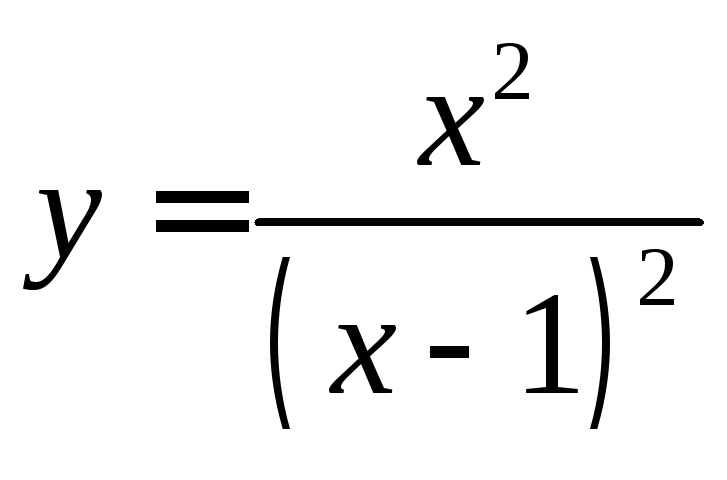6. .

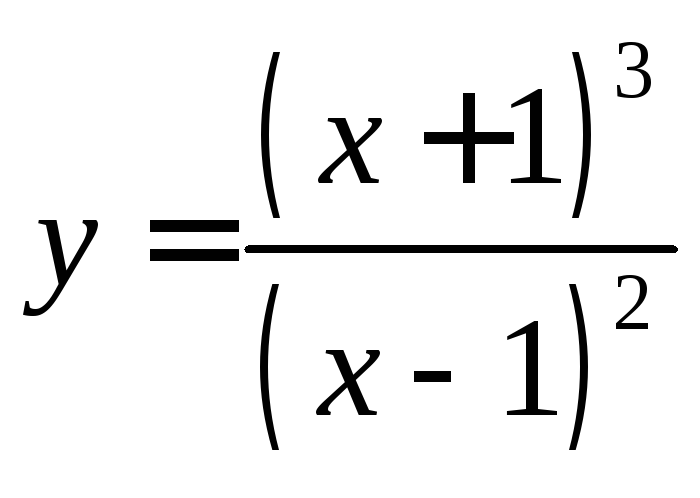7. .

8. .

9. .

10. .

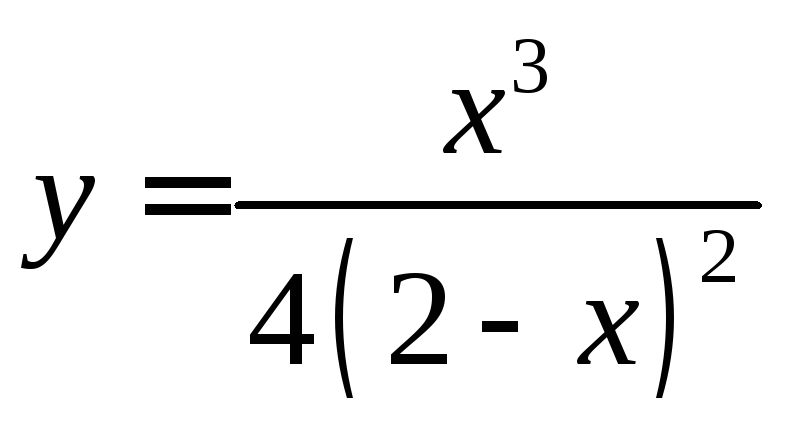11. .

12. .

13. .