4.1.4. Критерий максимума правдоподобия

Положим, наблюдателю известны только функции правдоподобия

и . В качестве критерия принятия решения о верности гипотезыН₁ выберем такое разбиение выборочного пространства , которое обеспечило бы наибольшее значение функции правдоподобия при верности гипотезыН₁, т.е. к выборочному подпространству отнесем те выборки , которые обеспечивают наибольшее значение функции правдоподобияпри верности гипотезыН₁. В этом случае критерий максимума правдоподобия принимает вид

, (4.15)

т. е. из всего множества возможных выборок выбираются только те выборки (и они образуют подмножество ), которые удовлетворяют неравенству (4.15). Сравнивая вероятности получения выборки при различных состояниях источника, отдадим предпочтение той гипотезе, для которой соответствующая вероятность больше.

Из соотношения (4.15) получим правило принятия решения по критерию максимума отношения правдоподобия, (МП),

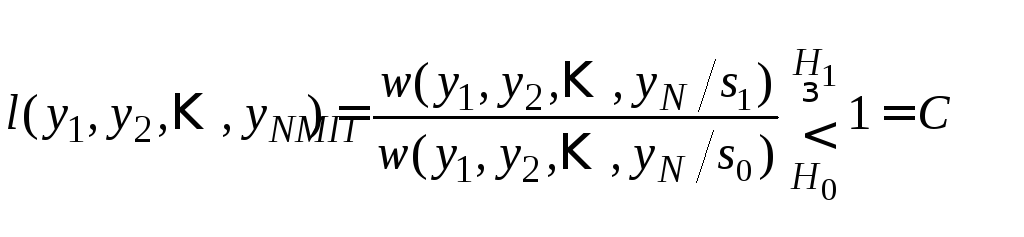. (4.16)

Если в выражении (4.14) положить ==0.5, получим правило обработки по критерию максимума правдоподобия.

4.1.5. Критерий Неймана-Пирсона

Рассмотренные ранее критерии принятия решения не использовали вероятности ошибок ипри разбиении множествана подмножестваG₀ и G₁, т.е. вероятности ошибок рассчитывались после разбиения множества на подмножестваG₀ и G₁ . В критерии Неймана-Пирсона вероятности ошибок  и  играют ключевую роль. Согласно критерию Неймана-Пирсона при априорно заданной вероятности ошибки первого рода  (уровень значимости) и заданном объеме выборки N находится такая критическая область значений , для которой вероятность 1-  (мощность критерия) принимает наибольшее значение.

Зафиксируем вероятность ошибки . Существует множество критических подмножеств , для которых вероятность ошибки одна и та же, т.е.

,

но вероятности правильного решения для различных критических подмножеств различны.

По теореме Неймана-Пирсона среди всех возможных критических множеств , для которых вероятность ошибки первого рода равна ^*, вероятность правильного решения 1- принимает наибольшее значение для критического подмножества , состоящей из всех тех точек y₁,y₂,...,y_N , для которых

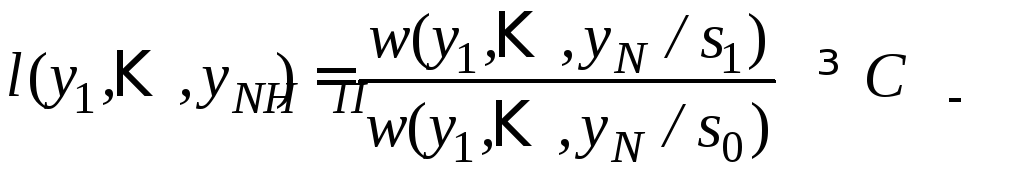. (4.17)

Порог определяется из условия

. (4.18)

Доказательство теоремы Неймана-Пирсона основано на методе неопределенных множителей Лагранжа, который используется для поиска условных максимумов и минимумов. Зафиксируем вероятность ошибки первого рода = const и составим функцию Лагранжа.

. (4.19)

Условие является ограничением,С – неопределенный множитель. Минимизируется функция - вероятность ошибки второго рода , рассматриваемая как функция выборочных значений. В теории оптимизации доказывается, если функцияпринимает минимальное значение на множестве значений, то и минимизируемая величинапринимает минимальное значение, при выполнении условия, на тех же самых выборках. Минимизируем функцию выбором множества . Вероятностьявно не зависит от области, поэтому удобно оперировать величиной. Тогда

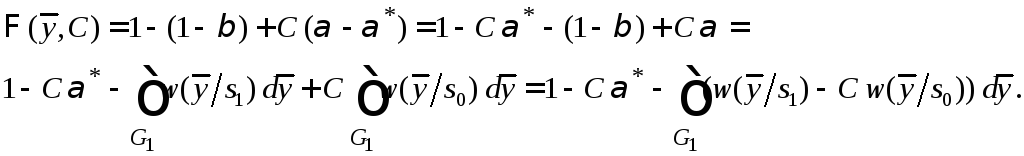
Функция будет достигать минимума при условии, что к области интегрированияотнесены все те значения выборокиз множества, которые обеспечивают не отрицательность подынтегрального выражения⁵, а именно

. (4.20)

Ввиду того, что выбирается множество , при выполнении неравенства (4.20) принимается гипотеза. То есть из (4.20) следует, что

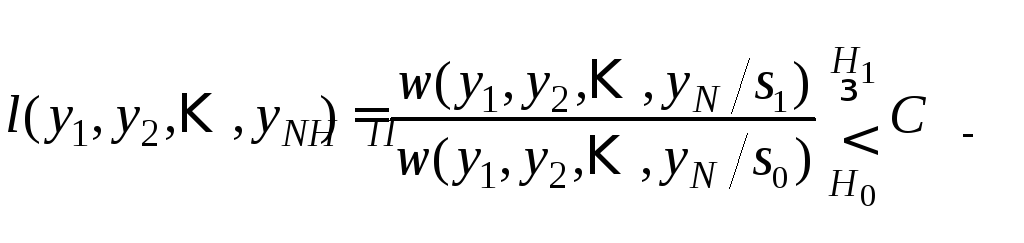. (4.21)

Порог ищется из условия

. (4.22)

Выражение (4.21) является правилом обработки выборочных значений .