5.3 Применение функционала отношения правдоподобия для обнаружения сигнала со случайной фазой

Рассмотрим модель квазидетерминированного сигнала , фаза которогораспределена равномерно в интервале:

,

амплитуда и частотадетерминированные величины и известны наблюдателю. Сигналпринимается на фоне белого шумасо значениями, распределёнными по нормальному закону:

.

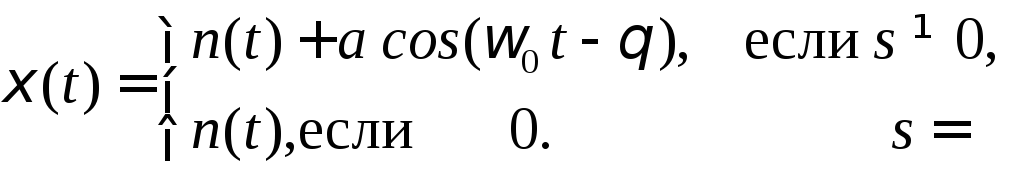Реализация принятого сигнала

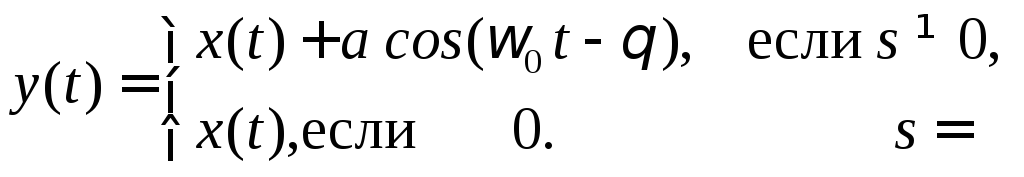
Для проверки гипотезы о наличии или об отсутствии сигнала в принятой реализации необходимо вычислить функционал отношения правдоподобия:

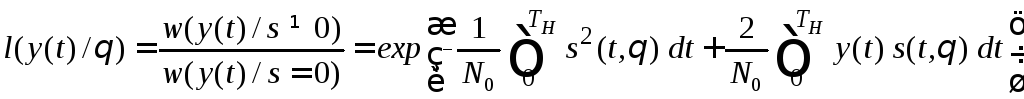. (5.25)

Однако функционал отношения правдоподобия зависит не только от реализации, но и от случайной величины. Чтобы избавиться от влияния значений случайной величины, усреднимпо всем возможным реализациям случайной величины:

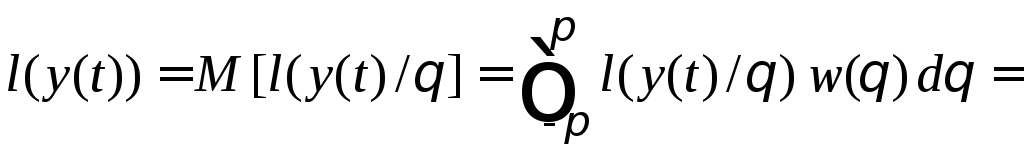
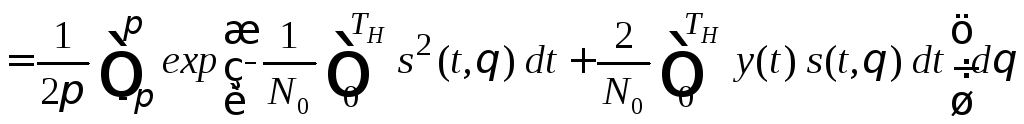. (5.26)

Рассмотрим интегралы в показателе экспоненты. Ввиду того, что фаза не является энергетическим параметром и , первый интеграл не зависит оти будет равен энергии процесса. Тогда

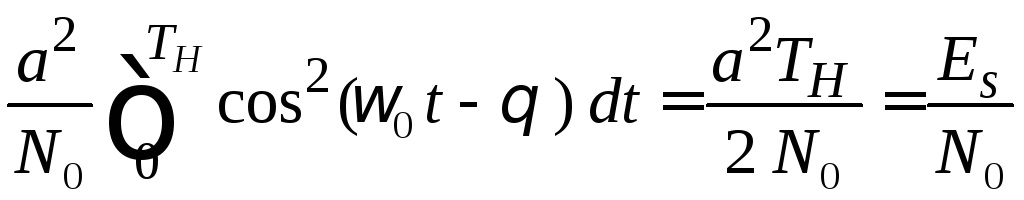. (5.27)

Второй интеграл в (5.26) является корреляционным интегралом

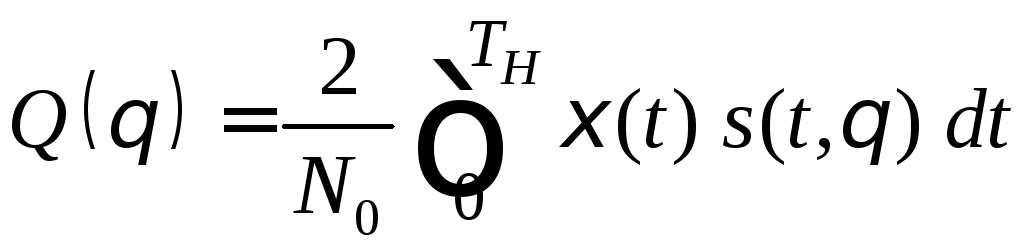(5.28)

со значением .

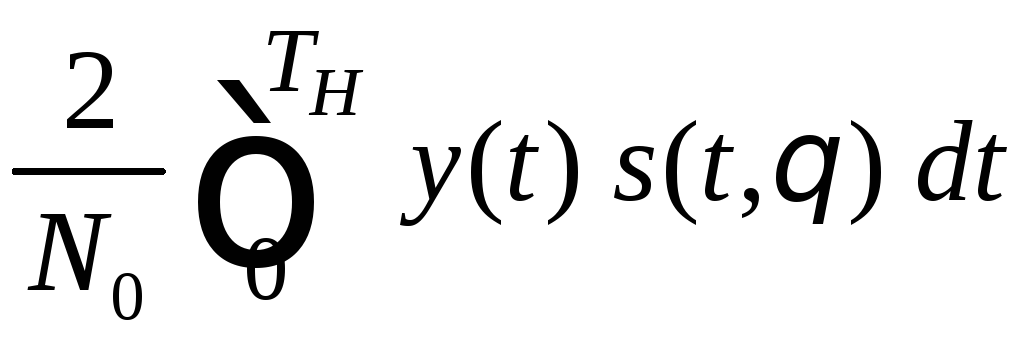Преобразуем интеграл (5.28), приведя его к виду

=

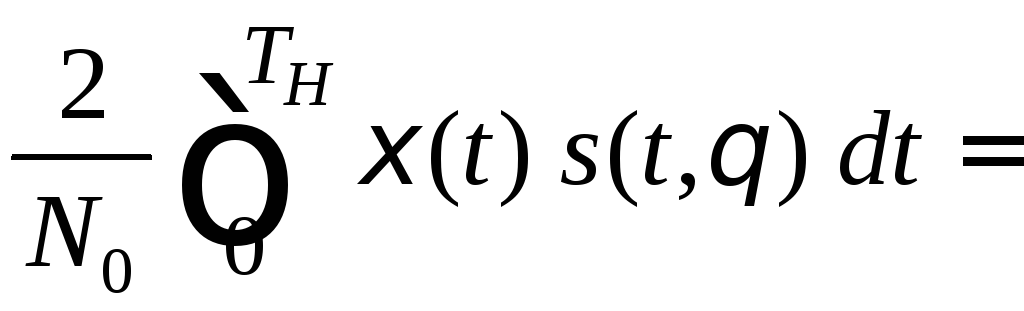
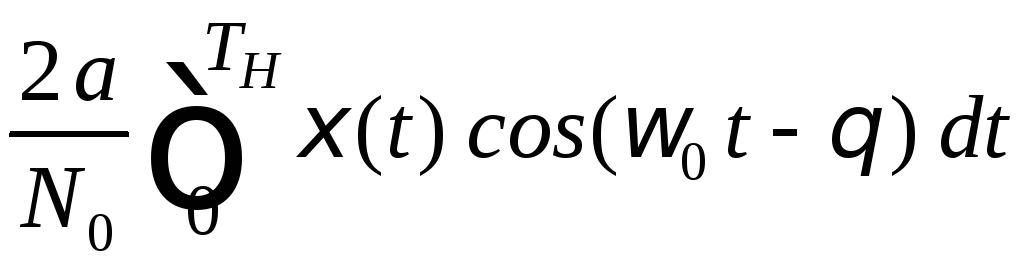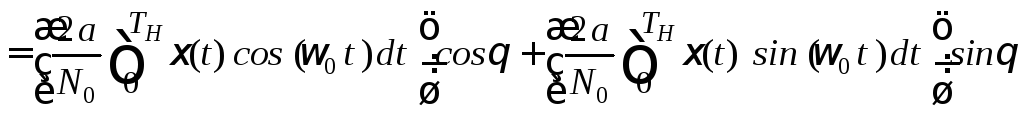. (5.29)

Обозначим

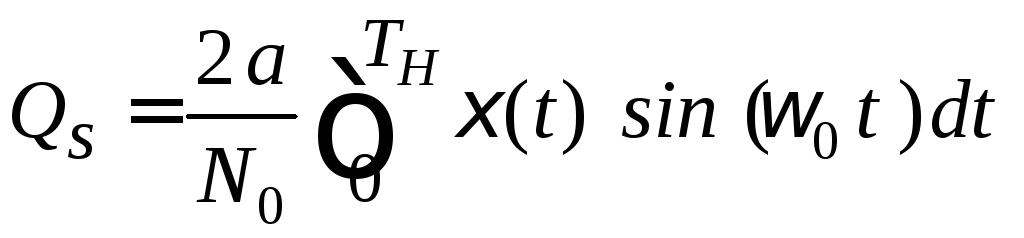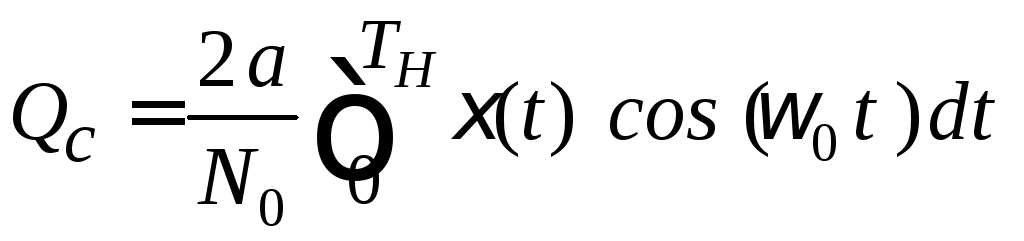, (5.30)

со значениями

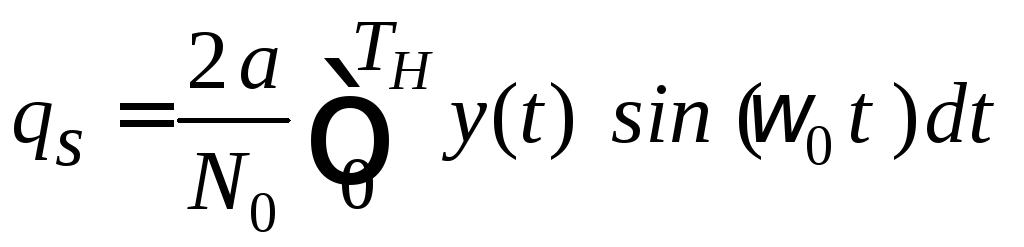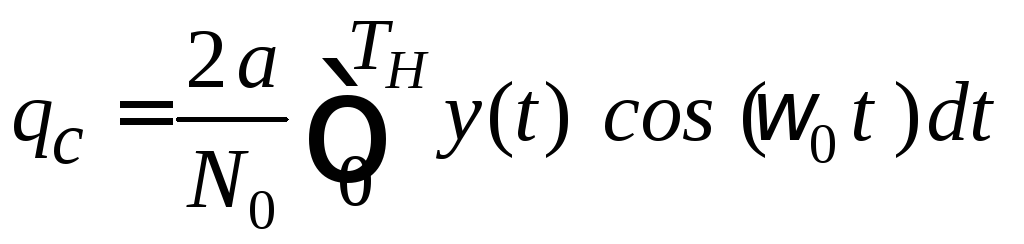, . (5.31)

Подставим ив (5.29)

. (5.32)

Введём новые случайные величины и, не зависящие отв явном виде, при помощи преобразования

, (5.33)

со значениями

, (5.34)

Геометрическая интерпретация составляющих иприведена на рисунке 5.5. Косинуснаяи синуснаясоставляющие будут значениями случайных величин, так как они зависят от реализации. Следовательно, и модуль вектора, и фазабудут реализациями случайных величин. Переход от декартовых координат к полярным координатам позволяет рассмотреть отдельно модуль и фазу корреляционного интеграла , (5.29). Подставив величины ив (5.32) приведём корреляционный интеграл (5.28) к виду

(5.35)

со значениями

. (5.36)

Подставим (5.27) и (5.36) в выражение (5.26)

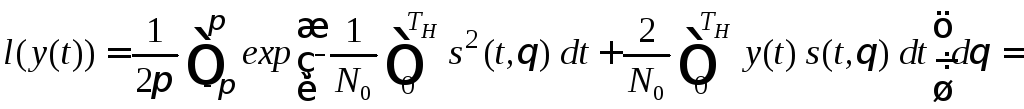
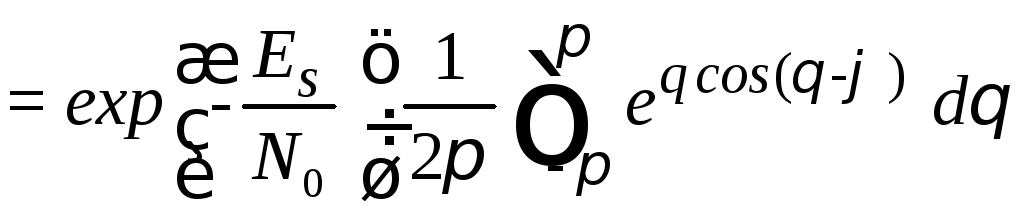. (5.37)

Интеграл после заменызапишется как

.

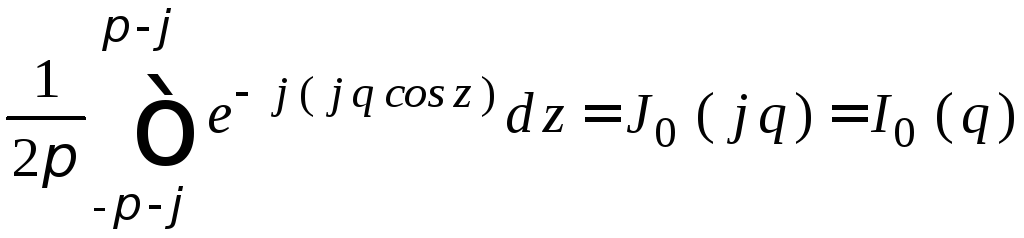Интеграл – функция Бесселя первого рода нулевого порядка от мнимого аргумента, он табулирован, а в специальных вычислительных пакетах приведены программы его вычисления. Подставим функцию Бесселя в (5.37) и получим решающее правило

, (5.38)

где – безразмерная величина и вычисляется по (5.34).

Для употребления правила обработки удобнее прологарифмировать функционал отношения правдоподобия и сравнить его с порогом, рассчитанным по выбранному критерию

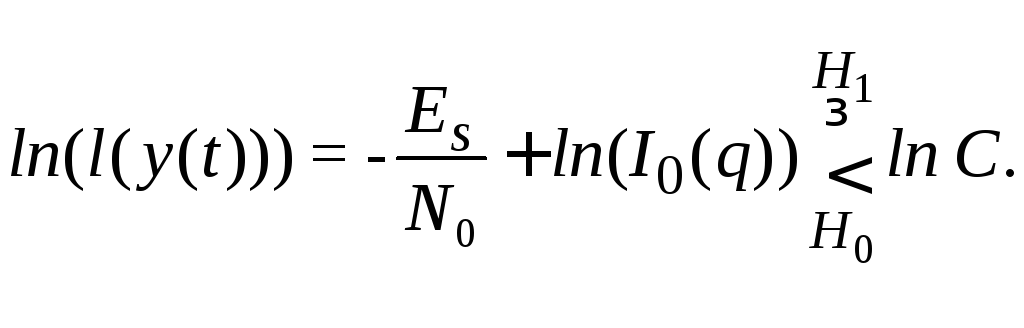(5.39)

Из теории специальных функций известно, что

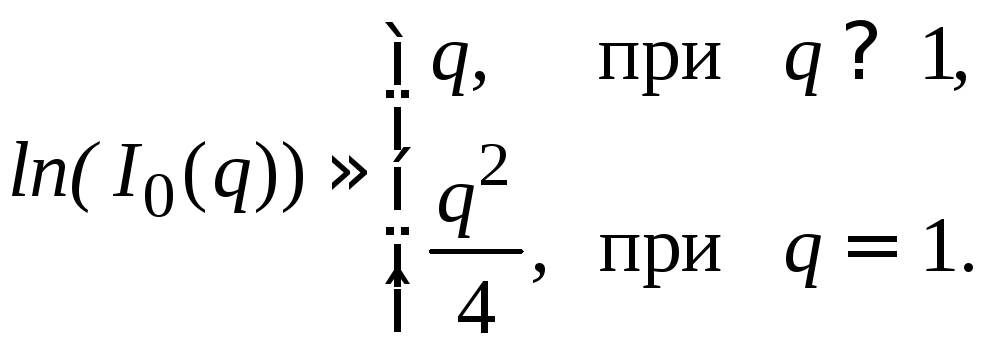
Л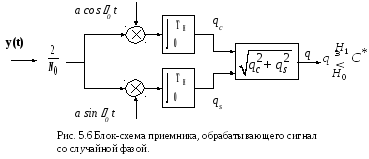инейная аппроксимация величинысоответствует большим значениям сигнал/шум, а квадратичная аппроксимация – малым отношениям сигнал/ шум. Положим, имеем тот случай, когда можно применить линейную аппроксимацию. Тогда правило обработки реализациипримет вид

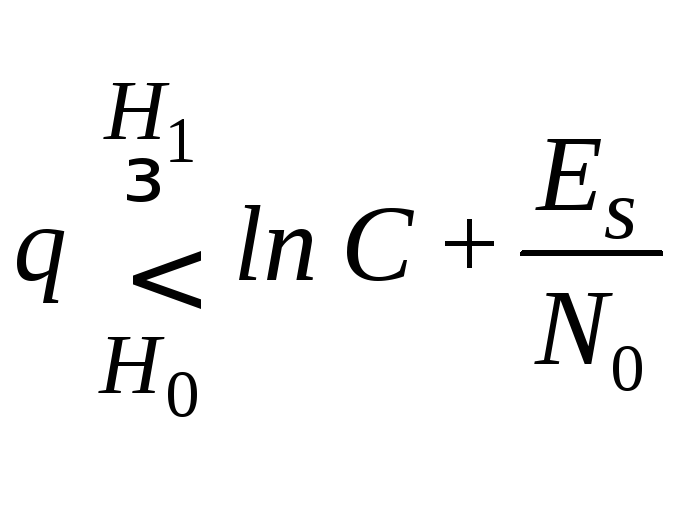или , (5.40)

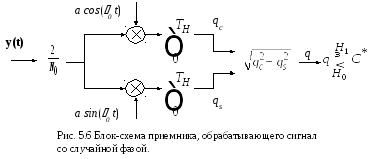
которое можно реализовать, используя величины и, (5.31). Блок-схема реализации приемника, обрабатывающего сигнал со случайной фазой приведена на рисунке 5.6.