
- •1. Введение
- •2. Типы решаемых задач
- •3. Проверка статистических гипотез
- •4. Критерии качества и правила принятия решений
- •4.1. Проверка двухальтернативных гипотез
- •4.1.1. Критерий Байеса
- •4.1.2. Минимаксный критерий
- •4.1.3. Критерий максимума апостериорной вероятности
- •4.1.4. Критерий максимума правдоподобия
- •4.1.5. Критерий Неймана-Пирсона
- •4.1.6. Последовательный критерий отношения вероятностей (Последовательный анализ Вальда)
- •4.1.7. Различение сигналов
- •5. Обработка непрерывных сигналов
- •5.1 Функционал правдоподобия
- •5.2 Применение функционала отношения правдоподобия для обнаружения полностью известного сигнала
- •5.3 Применение функционала отношения правдоподобия для обнаружения сигнала со случайной фазой
- •5.3.1. Расчет вероятностей ошибок
- •6. Оценка параметров сигнала
- •6.1. Свойства оценок параметров сигнала
- •6.2 Неравенство Рао-Крамера
- •7. Применение функционала отношения правдоподобия для оценки параметров сигнала
- •7.1. Оценка временного положения сигнала
- •7.2 Обработка пачки сигналов
- •7.3 Реализация алгоритма оценки временного положения сигнала
- •7.3.1 Корреляционный приёмник
- •7.3.2 Согласованный фильтр
- •Библиография
6.2 Неравенство Рао-Крамера
Знание
дисперсии
![]() оценки
оценки![]() ,
полученной по некоторому правилу,
позволяет судить о мере расхождения
истинного значения параметра
,
полученной по некоторому правилу,
позволяет судить о мере расхождения
истинного значения параметра![]() и его оценки
и его оценки![]() .
Однако равна ли дисперсия
.
Однако равна ли дисперсия![]() минимальной дисперсии – неизвестно.
С.Р. Рао и Г. Крамером получена нижняя
граница дисперсии
минимальной дисперсии – неизвестно.
С.Р. Рао и Г. Крамером получена нижняя
граница дисперсии![]() оценки
оценки![]() .
.
Положим,
![]() – выборка в моменты времени,
– выборка в моменты времени,![]() ,
сигнал и шум аддитивны:
,
сигнал и шум аддитивны:![]() ,
,
![]() –выборочные
значения в моменты времени
–выборочные
значения в моменты времени
![]() ,
,![]() ,
,
![]() –функция
правдоподобия.
–функция
правдоподобия.
Запишем
условие нормировки
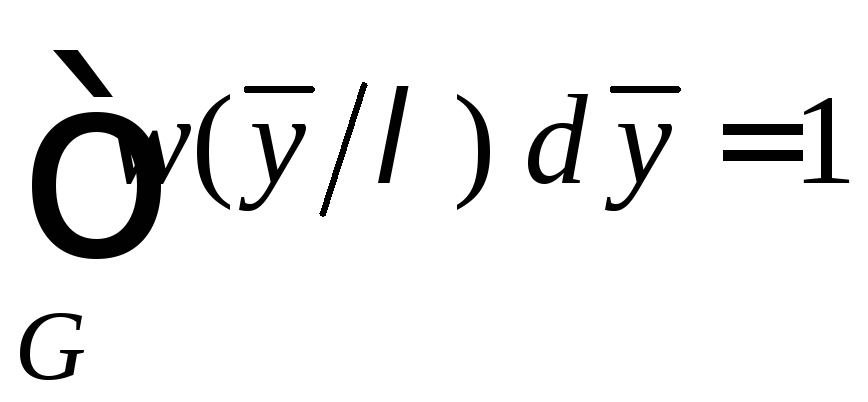 и продифференцируем его по параметру
и продифференцируем его по параметру![]() .
Переставляя операции дифференцирования
и интегрирования,
.
Переставляя операции дифференцирования
и интегрирования,
получим:
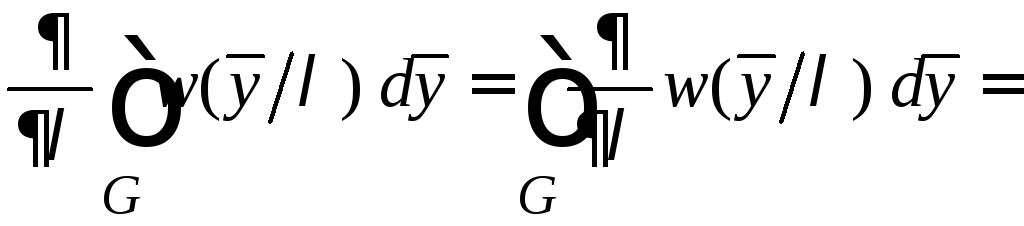
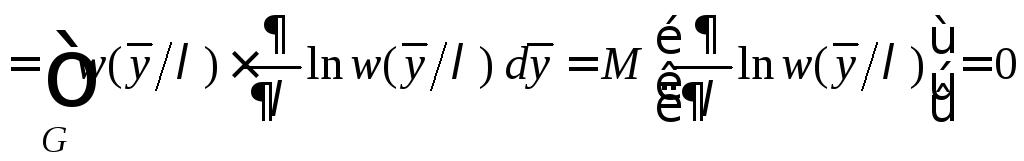 (6.2)
(6.2)
Оценка
![]() является функцией выборочных значений,
то есть
является функцией выборочных значений,
то есть![]() и согласно свойствам математического
ожидания преобразования случайной
величины имеем
и согласно свойствам математического
ожидания преобразования случайной
величины имеем
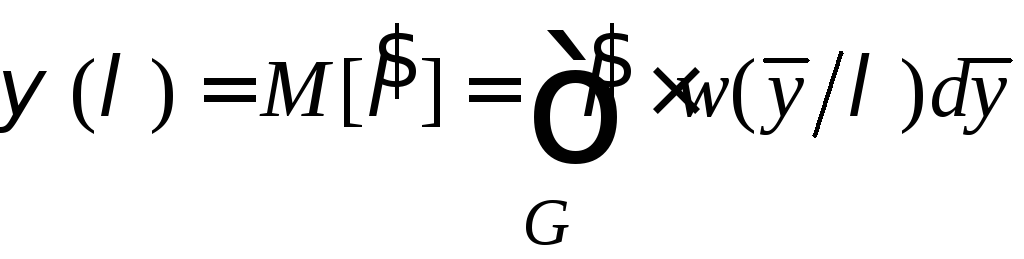 ,
,
то
есть математическое ожидание оценки
![]() является функцией параметра
является функцией параметра![]() .
.
Её
производная по
![]() имеет вид
имеет вид
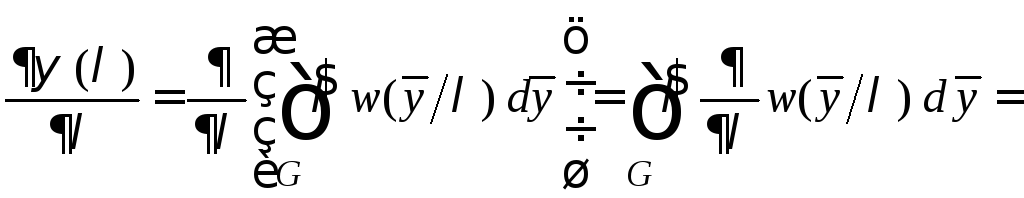
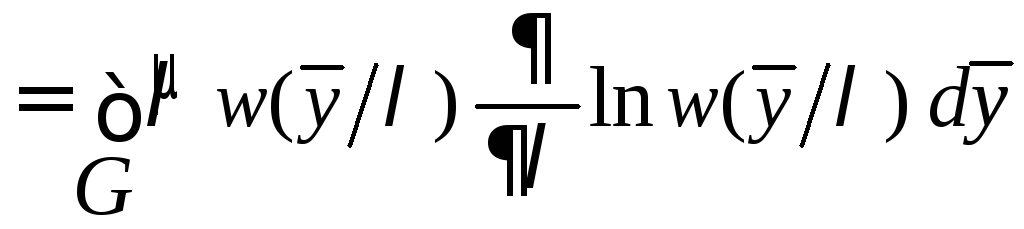 .
(6.3)
.
(6.3)
Помножим
выражение (6.2) на функцию
![]()
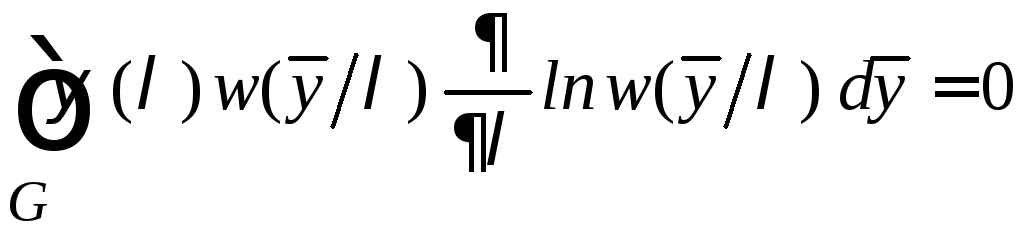 (6.4)
(6.4)
Учитывая, что последнее выражение (6.4) равно нулю, вычтем (6.4) из (6.3):
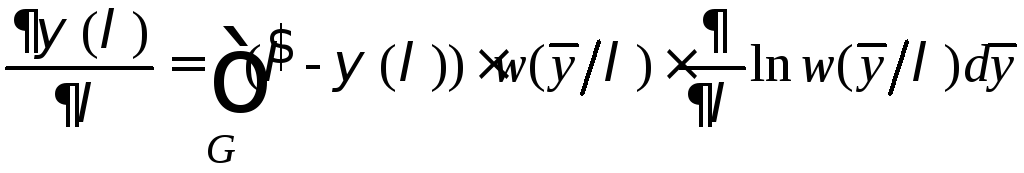 .
.
Воспользуемся неравенством Коши-Буняковского
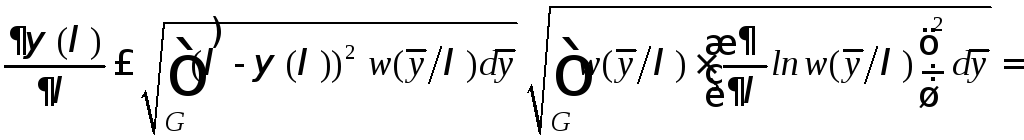
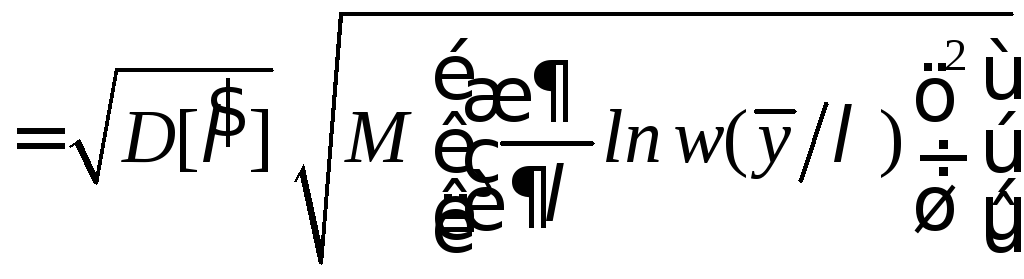 .
(6.5)
.
(6.5)
Откуда непосредственно получаем
 (6.6)
(6.6)
Получили неравенство Рао-Крамера. Правая часть неравенства позволяет оценить минимальную величину дисперсии, которую можно достичь при различных правилах оценки параметра.
Рассмотрим свойства неравенства Рао-Крамера.
1) Из неравенства Коши-Буняковского (6.5) знак равенства в выражении (6.6) получается, если
![]() ,
(6.7)
,
(6.7)
где А - некоторая постоянная величина, не зависящая от наблюдений.
Если
условие (6.7) выполняется, то оценка
![]() является эффективной оценкой параметра
является эффективной оценкой параметра![]() и её дисперсия равна
и её дисперсия равна
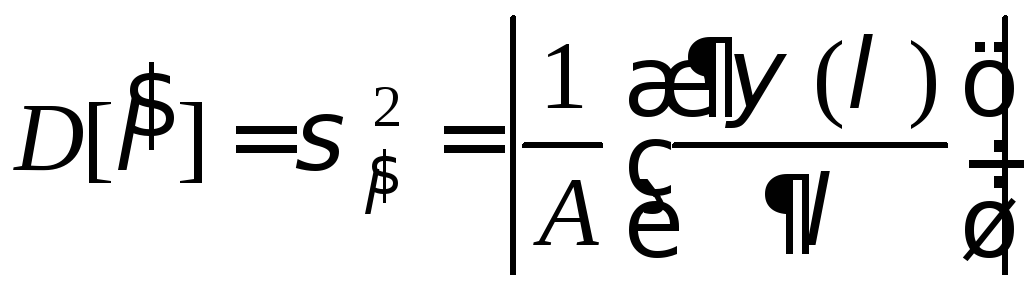 .
(6.8)
.
(6.8)
2)
В числителе неравенства Рао-Крамера
(6.6) стоит квадрат производной от
математического ожидания оценки
![]() .
Если оценка
.
Если оценка![]() – несмещённая, т.е.
– несмещённая, т.е.![]() ,
то
,
то![]() и её дисперсия оценки равна
и её дисперсия оценки равна
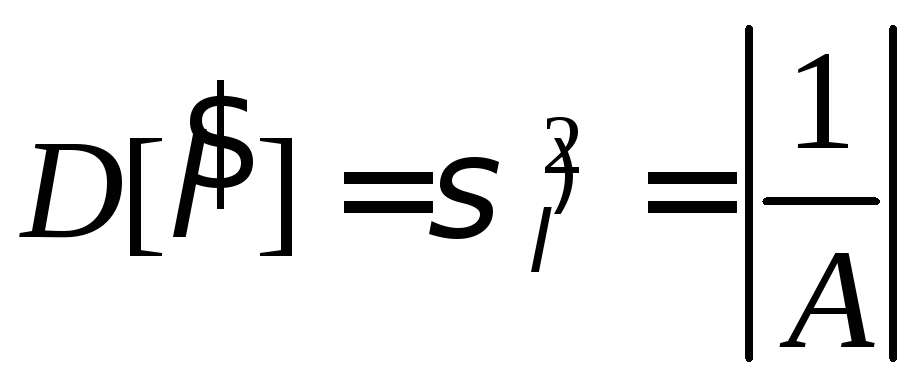 .
(6.9)
.
(6.9)
Покажем,
что в этом случае 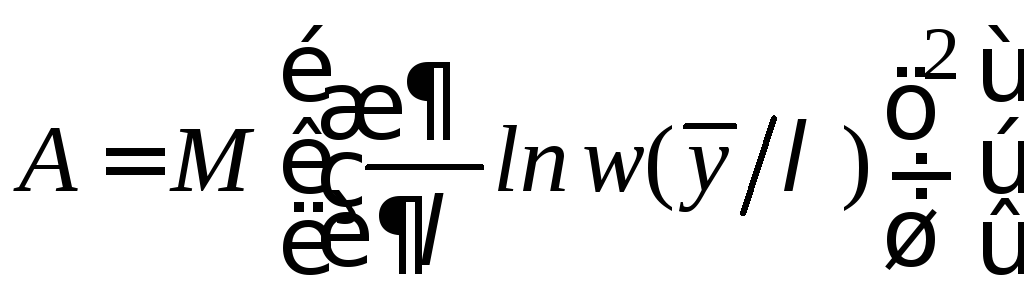 .
.
Возведем обе части равенства (6.7) в квадрат и приложим оператор математического ожидания к обеим частям полученного равенства
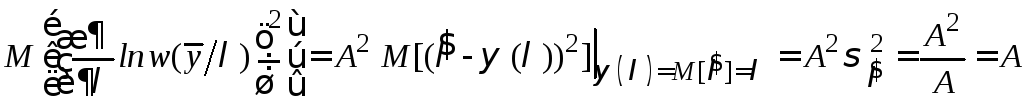 .
.
В
общем случае коэффициент
![]() может зависеть от измеряемого параметра
может зависеть от измеряемого параметра![]() .
Величина
.
Величина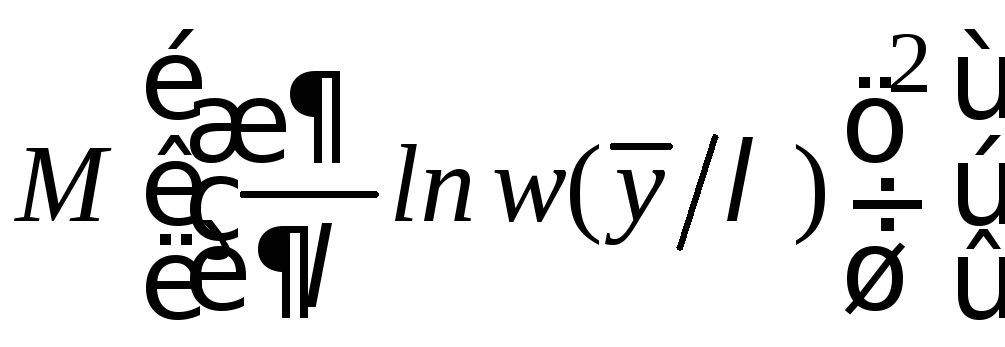 определяет меру информации, содержащейся
в выборке
определяет меру информации, содержащейся
в выборке![]() ,
и называетсяколичеством
информации,
содержащейся в выборке (введена Р.
Фишером).
,
и называетсяколичеством
информации,
содержащейся в выборке (введена Р.
Фишером).
3) Доказательство выражения (6.8).
Положим, выполняется условие (6.7). Возведем в квадрат обе части равенства (6.7) и вычислим математическое ожидание от обеих частей:
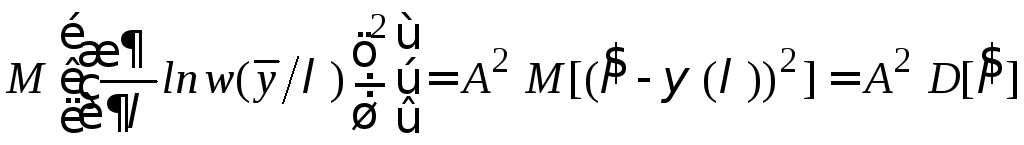 .
.
Учитывая условие (6.7) и предыдущее выражение, запишем неравенство Рао-Крамера в виде равенства
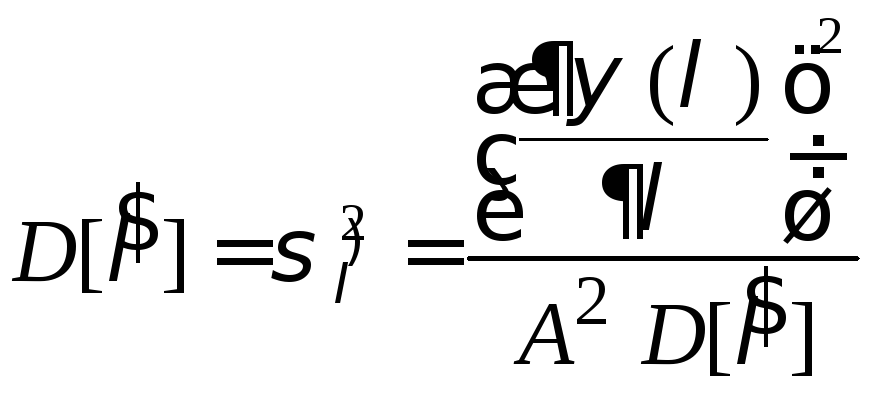 .
.
Из этого выражения получим
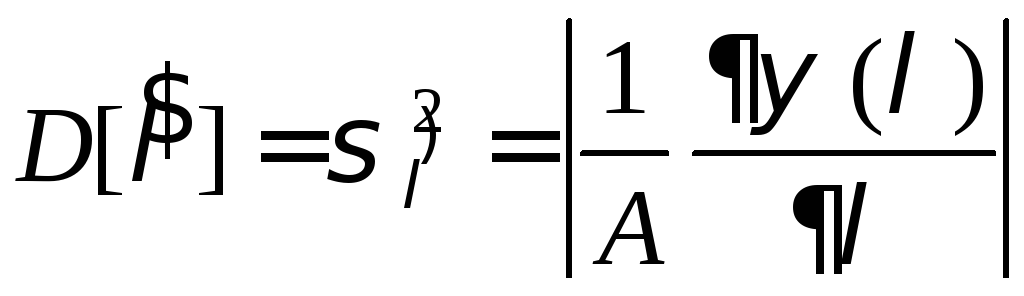 .
(6.8)
.
(6.8)
4)
Иногда трудно бывает вычислить знаменатель
неравенства Рао-Крамера (6.6). Преобразуем
его. Для этого продифференцируем
выражение (6.2) по
![]() :
:

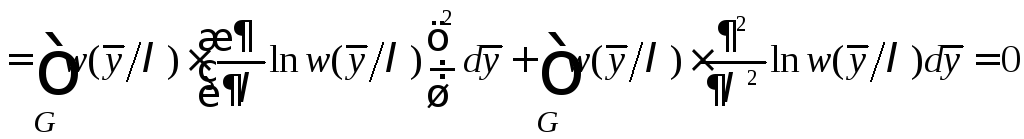 ,
,
или
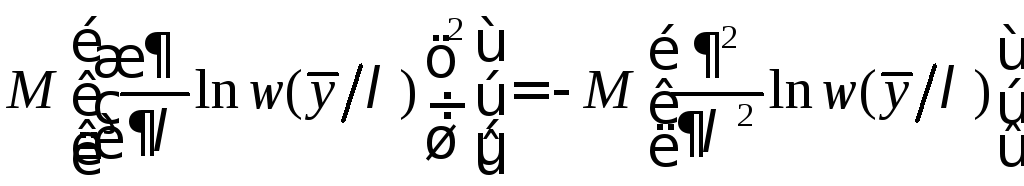 (6.10)
(6.10)
Подставим
(6.10) в (6.6) с учётом того, что
![]() ,
,
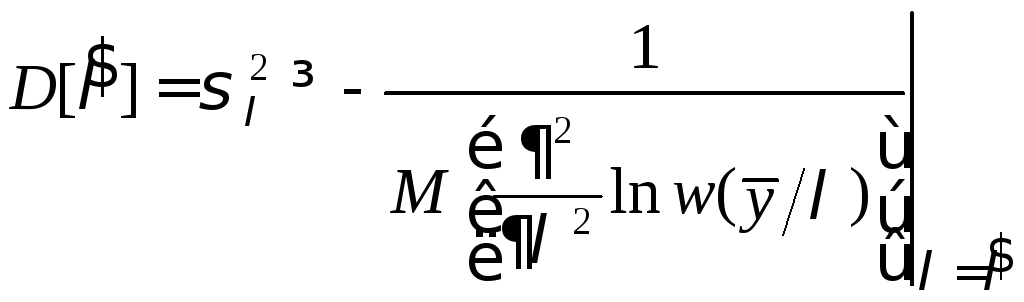 (6.11)
(6.11)
5)
Неравенство (6.11) получено для дискретного
представления
![]() реализации
реализации![]() случайного процесса
случайного процесса![]() .
Переходя к функционалу правдоподобия,
запишем
.
Переходя к функционалу правдоподобия,
запишем
 (6.12)
(6.12)
6) Как известно, в случае приема сигнала на фоне нормального белого шума функционал правдоподобия имеет вид
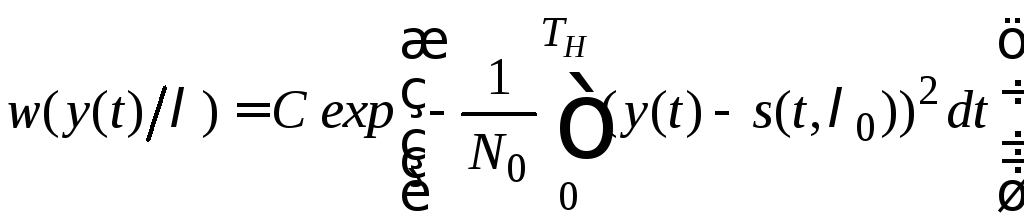 .
.
Положим
постоянная С
удовлетворяет условию
![]() .
Тогда логарифм функционала правдоподобия
равен
.
Тогда логарифм функционала правдоподобия
равен
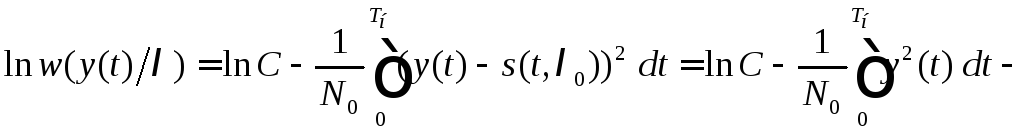
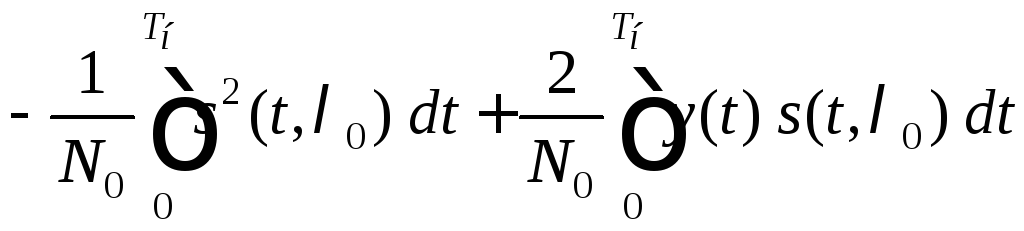 .
.
Если
параметр
![]() не энергетический, то
не энергетический, то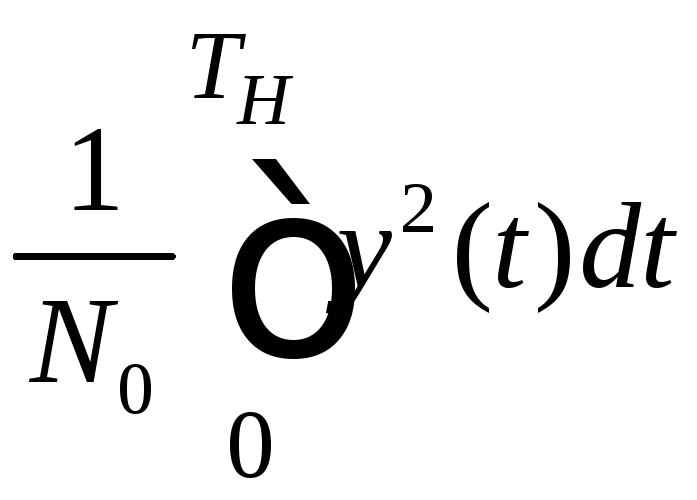 не зависит от
не зависит от![]() и получим, с учётом того, что
и получим, с учётом того, что![]() ,
,
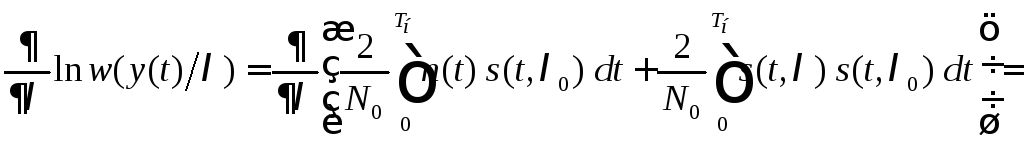
![]() (6.13)
(6.13)
Интегралы
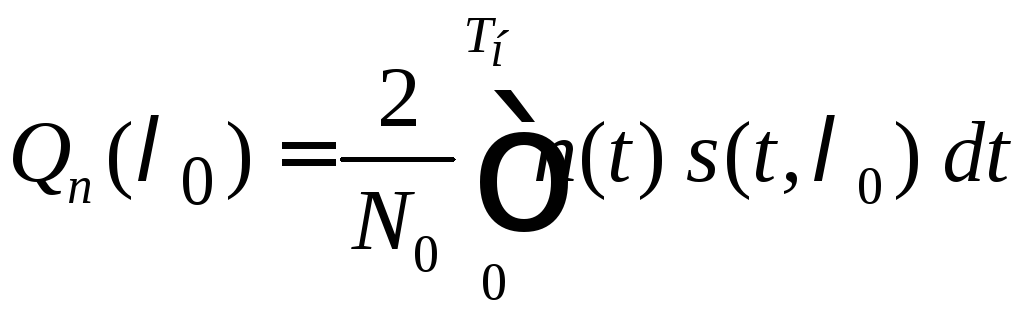 и
и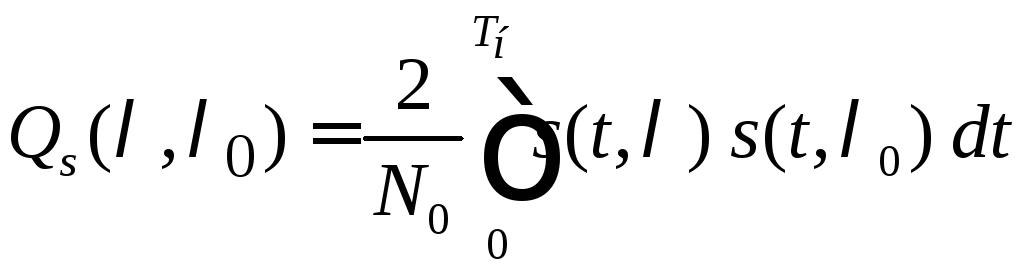 называютсяшумовой
и сигнальной
функциями
в применении к оценке параметра сигнала,
параметр
называютсяшумовой
и сигнальной
функциями
в применении к оценке параметра сигнала,
параметр
![]() можно менять в определенных пределах
согласно оцениваемому параметру, поэтому
сигнал
можно менять в определенных пределах
согласно оцениваемому параметру, поэтому
сигнал![]() называетсяопорным
сигналом.
называетсяопорным
сигналом.
Дифференцируя
повторно выражение (6.13) по параметру
![]() ,
получим
,
получим
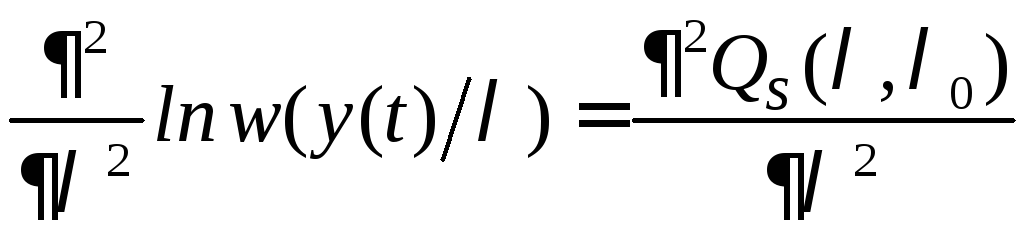 .
(6.14)
.
(6.14)
Теперь
нижнюю границу дисперсии оценки параметра
![]() можно представить как
можно представить как
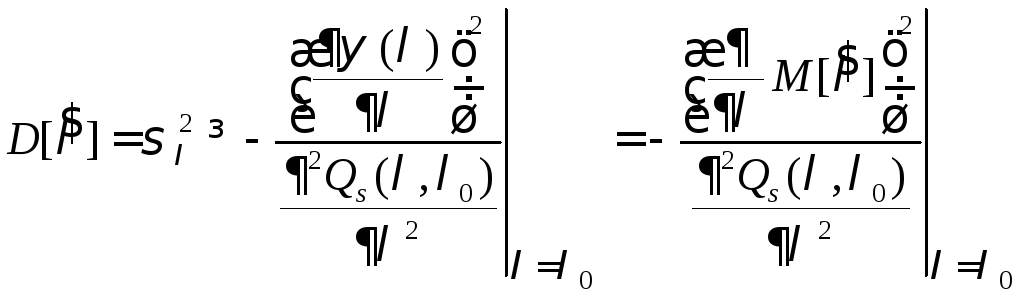 (6.15)
(6.15)
Знаменатель выражения (6.15) отражает кривизну сигнальной функции
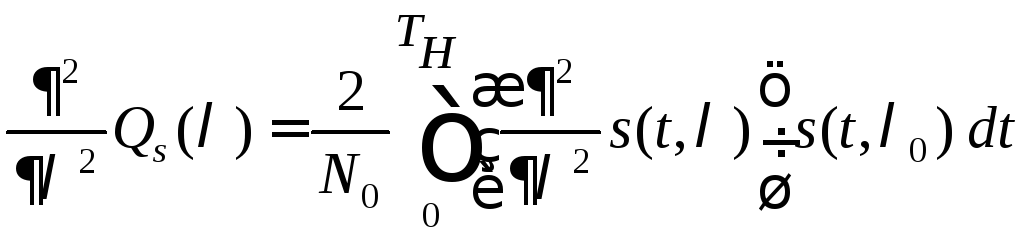 .
.
Чем
больше абсолютное значение кривизны
сигнальной функции в точке
![]() ,
тем меньше граница дисперсии, которую
можно достичь, выбрав наилучшее правило
оценки параметра
,
тем меньше граница дисперсии, которую
можно достичь, выбрав наилучшее правило
оценки параметра![]() .
.
7)
Положим, оценка
![]() принадлежит множеству оценок, для
которых математическое ожидание оценки
принадлежит множеству оценок, для
которых математическое ожидание оценки![]() можно выразить как
можно выразить как
![]() ,
(6.16)
,
(6.16)
где
![]() – смещение – детерминированная величина,
зависящая от истинного значения
– смещение – детерминированная величина,
зависящая от истинного значения
![]() .
Тогда неравенство Рао-Крамера примет
вид
.
Тогда неравенство Рао-Крамера примет
вид
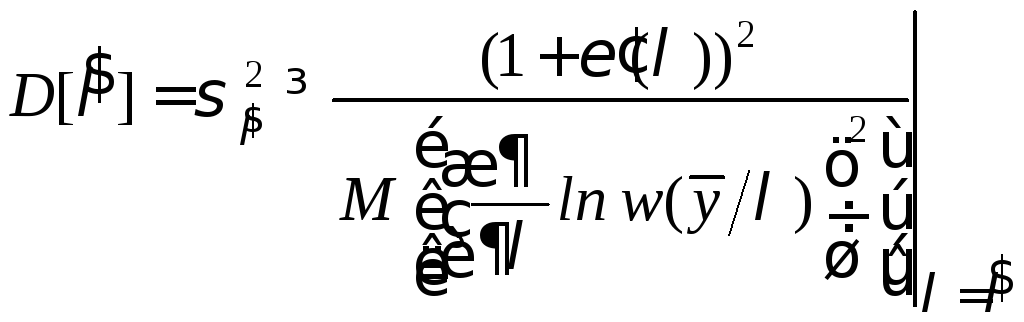 .
(6.17)
.
(6.17)
Нижняя граница неравенства зависит от величины
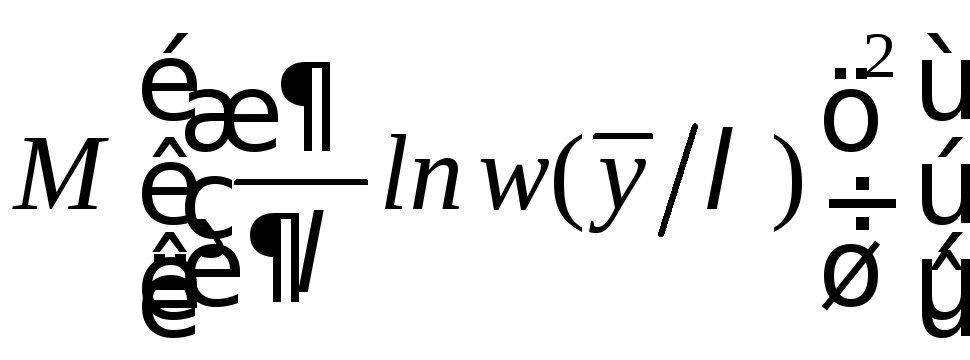 =
=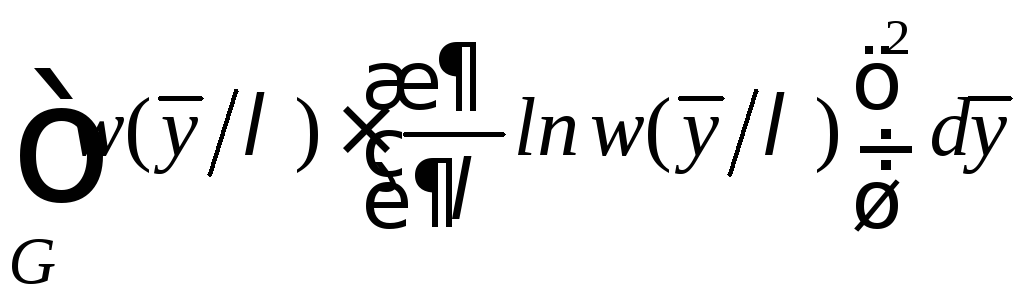 =
=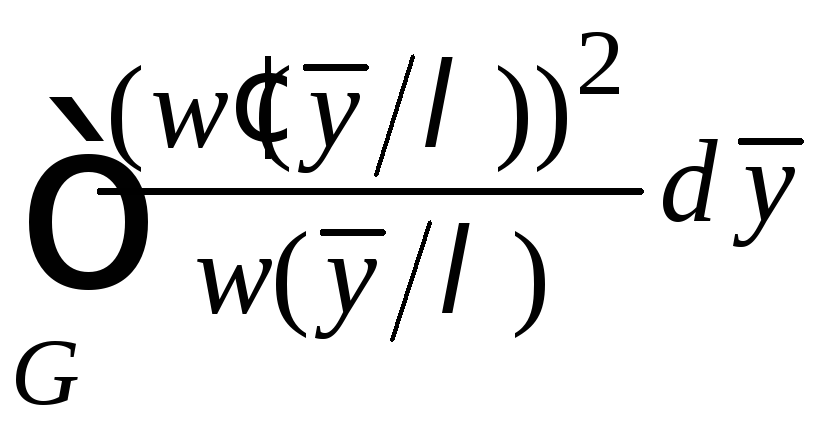 .
(6.18)
.
(6.18)
Из
последнего выражения видно, что величина
нижней границы зависит от поведения
производной
![]() .
В литературе (А.А Боровков, М.Дж. Кендалл
и А. Стьюарт) доказывается, что можно
получить нижнюю границу дисперсии,
меньшую, чем граница Рао-Крамера.
.
В литературе (А.А Боровков, М.Дж. Кендалл
и А. Стьюарт) доказывается, что можно
получить нижнюю границу дисперсии,
меньшую, чем граница Рао-Крамера.
Рассмотрим
примеры. Произведем оценку математического
ожидания и дисперсии нормального
распределения. Положим параметр
![]() (это может быть частота, задержка, и
т.д.) сигнала
(это может быть частота, задержка, и
т.д.) сигнала![]() имеет нормальное распределение с
математическим ожиданием
имеет нормальное распределение с
математическим ожиданием![]() и дисперсией
и дисперсией![]()
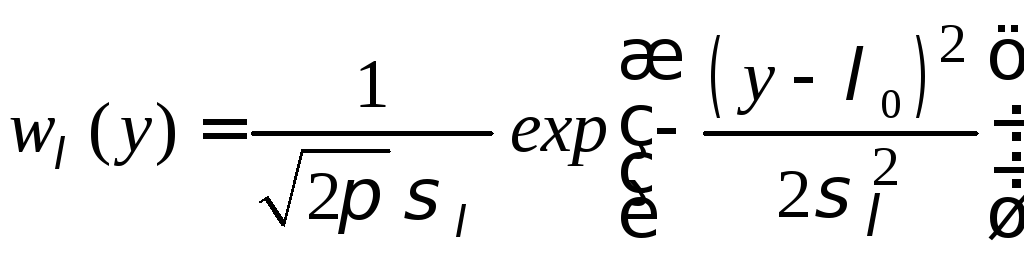 .
.
Пусть
в результате проведения эксперимента
получили последовательность независимых
случайных величин
![]() .
Необходимо оценить величину
.
Необходимо оценить величину![]() ,
если известно значение дисперсии
,
если известно значение дисперсии![]() .
Другой случай – оценить параметр
.
Другой случай – оценить параметр![]() ,
если неизвестно значение дисперсии
,
если неизвестно значение дисперсии![]() .
.
Пример
1. Произведем
оценку
![]() при известной дисперсии
при известной дисперсии![]() по критерию максимума функции правдоподобия
по критерию максимума функции правдоподобия![]() ,
имеющей вид
,
имеющей вид
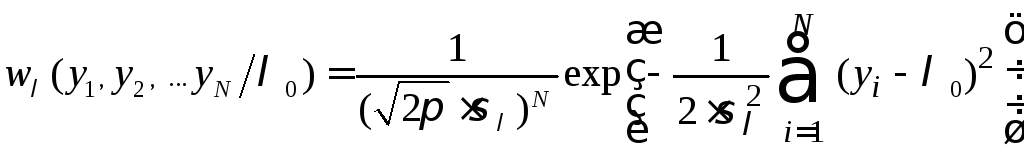 .
.
Используем
логарифм функции правдоподобия
![]() .
Необходимое условие максимума – это
.
Необходимое условие максимума – это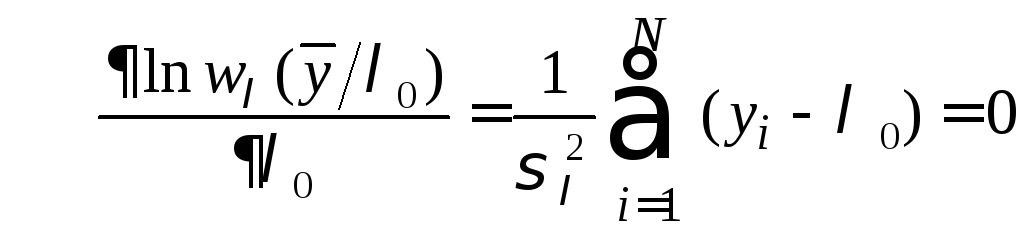 .
.
Решая
это уравнение относительно
![]() ,
получим
,
получим
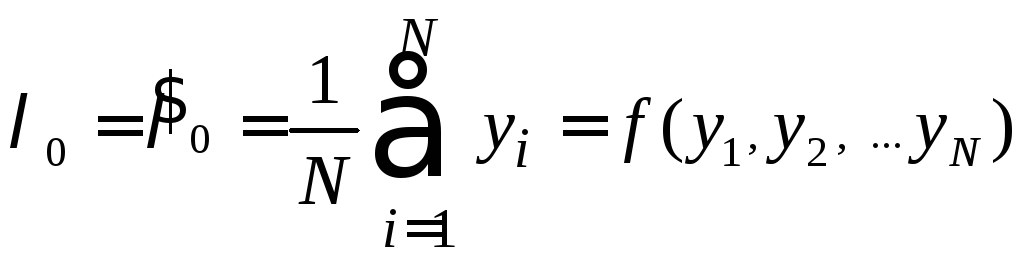
и
примем её в качестве оценки параметра
![]()
Рассмотрим свойства этой оценки.
а) Состоятельность. Необходимо проверить
![]() или
или
![]() .
.
Ввиду
того, что выборка
![]() взята из нормальной совокупности, каждый
член суммы распределён по нормальному
закону с математическим ожиданием
взята из нормальной совокупности, каждый
член суммы распределён по нормальному
закону с математическим ожиданием![]() и дисперсией
и дисперсией![]() .
Тогда и
.
Тогда и![]() распределена по нормальному закону с
математическим ожиданием
распределена по нормальному закону с
математическим ожиданием
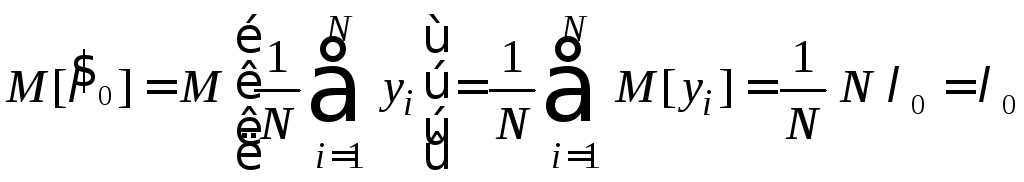 и
дисперсией
и
дисперсией
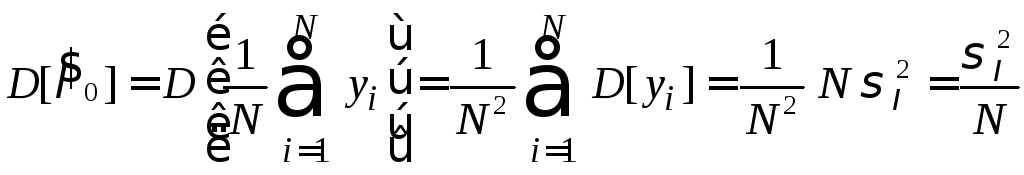 .
.
Рассмотрим вероятность
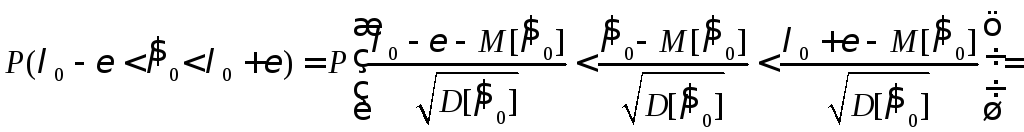
 .
.
С
увеличением числа экспериментов
![]() границы
границы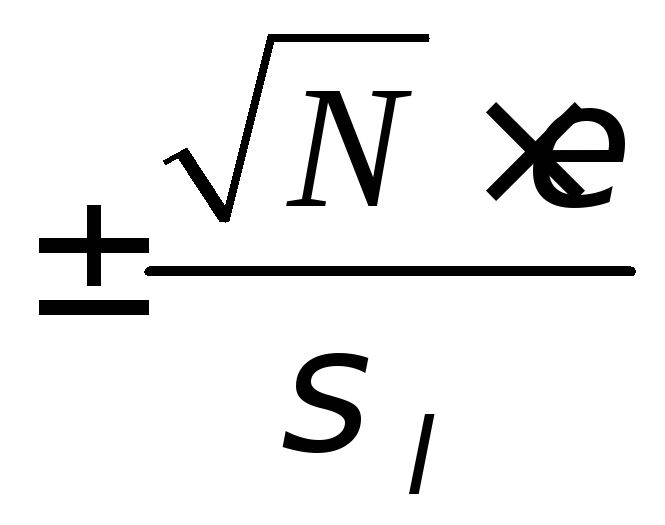 увеличиваются по абсолютной величине.
Таким образом, при
увеличиваются по абсолютной величине.
Таким образом, при![]() вероятность
вероятность![]() ,
т.е. оценка
,
т.е. оценка![]() – состоятельная.
– состоятельная.
б)
Смещение оценки. Из выражения
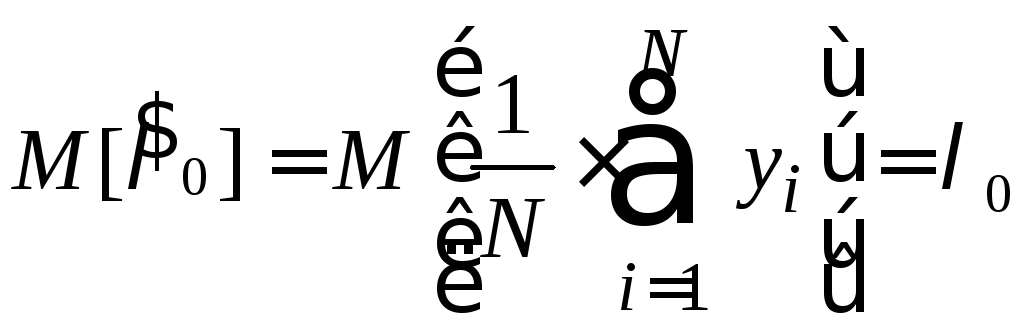 видно, что оценка
видно, что оценка![]() не смещена.
не смещена.
в) Эффективность. Вычислим границу Рао-Крамера. Для этого рассмотрим знаменатель неравенства Рао-Крамера
 .
.
Ввиду
того, что оценка
![]() несмещённая, а также в силу независимости
результатов эксперимента имеем
несмещённая, а также в силу независимости
результатов эксперимента имеем
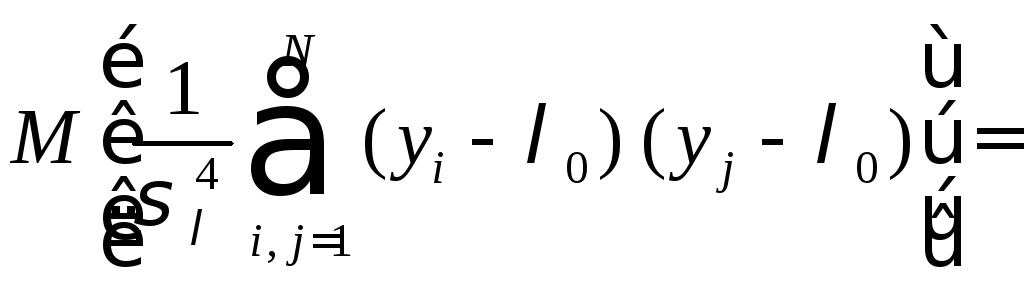
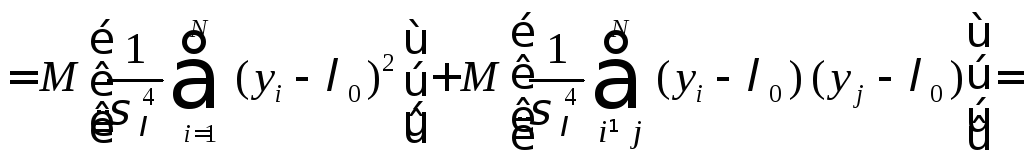
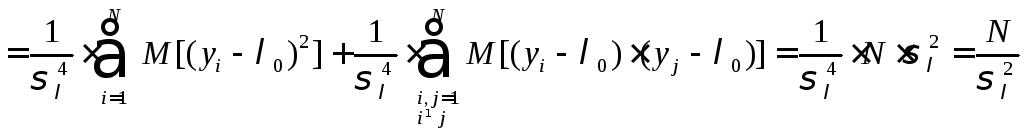 .
.
Тогда
неравенство Рао-Крамера примет вид
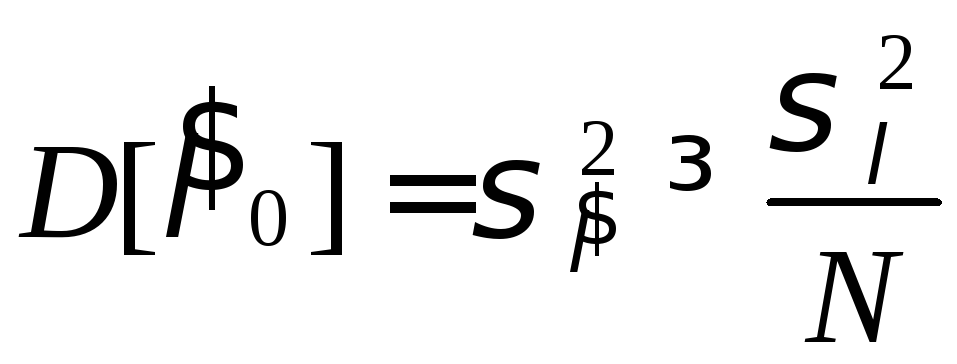 ,
но мы уже знаем, что
,
но мы уже знаем, что .
Как видим, нижняя граница дисперсии
оценки
.
Как видим, нижняя граница дисперсии
оценки![]() совпадает с дисперсией оценки. Таким
образом, оценка
совпадает с дисперсией оценки. Таким
образом, оценка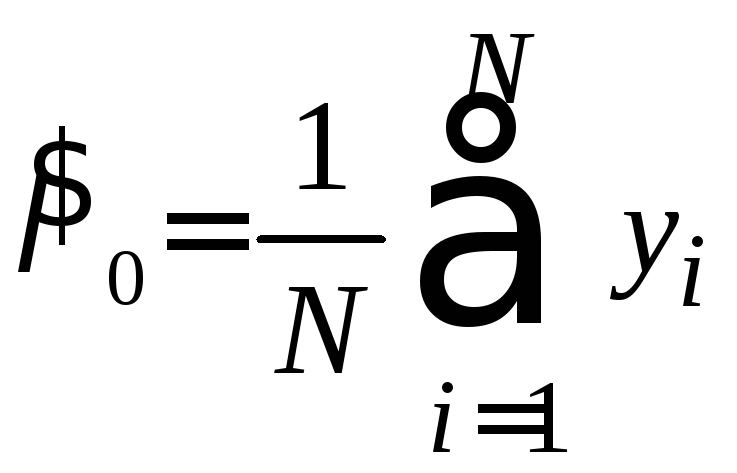 является эффективной, но она ещё и
достаточная по определению, так как
плотность распределения вероятности
является эффективной, но она ещё и
достаточная по определению, так как
плотность распределения вероятности
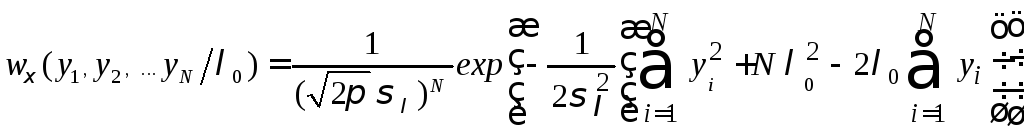
удовлетворяет условиям необходимости и достаточности
Пример
2. Произведём
оценку математического ожидания
![]() и дисперсии
и дисперсии![]() по критерию максимума функции
правдоподобия:
по критерию максимума функции
правдоподобия: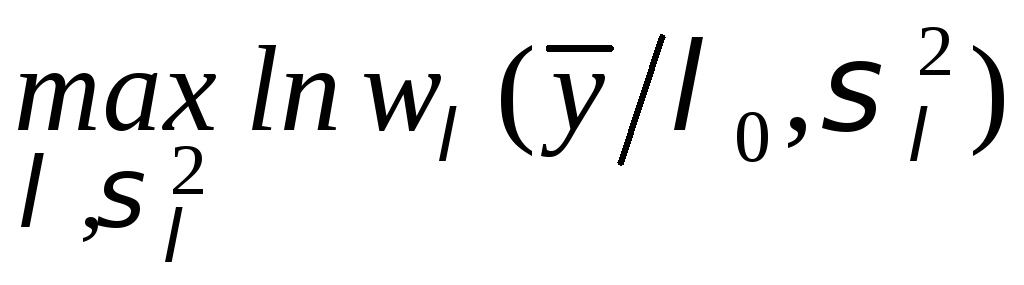 .
.
Логарифм функции правдоподобия имеет вид
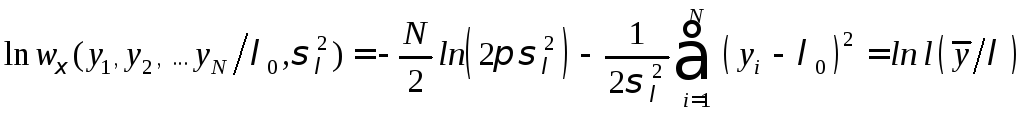
Беря
производную по
![]() и
и![]() и приравнивая их нулю, получаем систему
уравнений:
и приравнивая их нулю, получаем систему
уравнений:
![]()
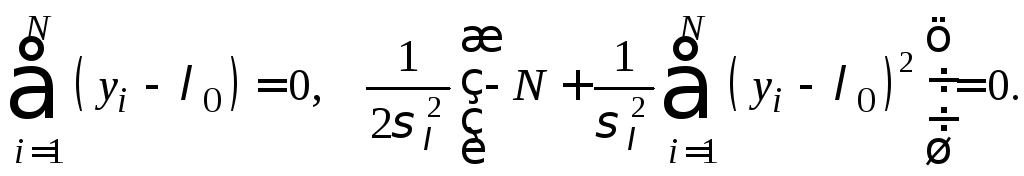
Откуда получаем оценки:
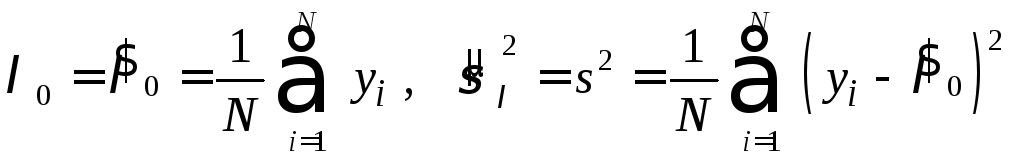 .
.
Рассмотрим
оценку дисперсии
![]() параметра
параметра![]() :
:
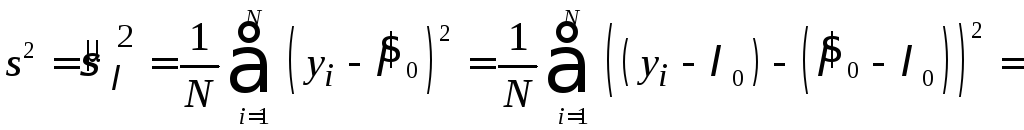

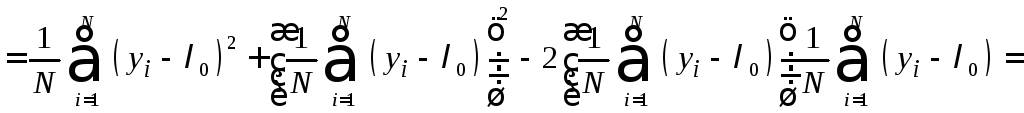
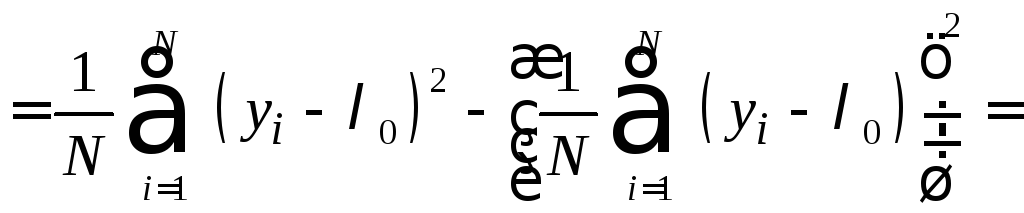
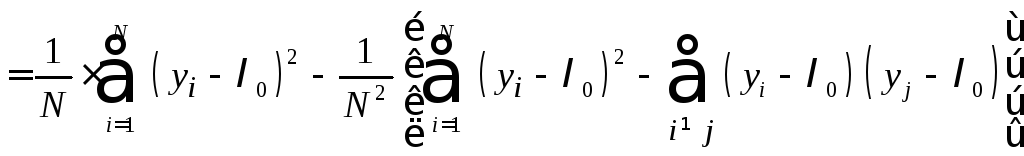 .
.
С
учетом того, что значения выборок взаимно
независимы, можно вычислить математическое
ожидание
![]()
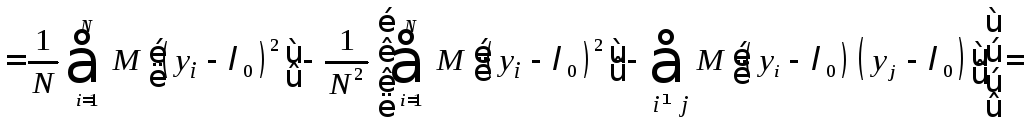
=
![]() .
.
Как
видно,
![]() не является несмещённой оценкой дисперсии
не является несмещённой оценкой дисперсии![]() .
Для получения несмещённой оценки
помножим
.
Для получения несмещённой оценки
помножим![]() на
на![]() :
:
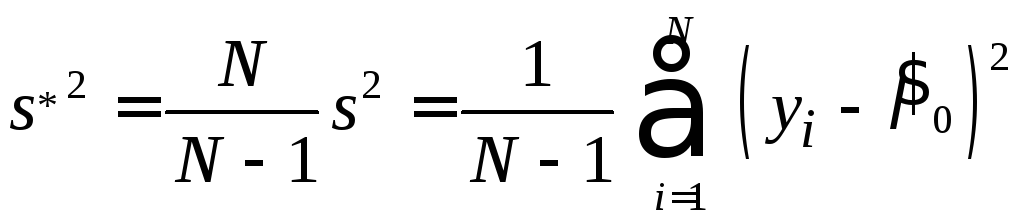 .
.
Математическое
ожидание
![]() равно
равно
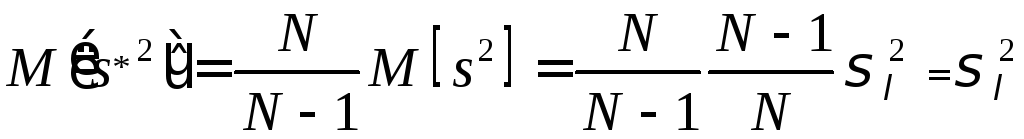 .
.
Откуда
видно, что оценка
![]() является несмещённой оценкой
является несмещённой оценкой![]() .
Разница в методах вычисления оценки
скажется лишь при малом числе экспериментов.
Когда
.
Разница в методах вычисления оценки
скажется лишь при малом числе экспериментов.
Когда![]() довольно велико отличие между
довольно велико отличие между![]() и
и![]() несущественно, то есть при
несущественно, то есть при![]() величина
величина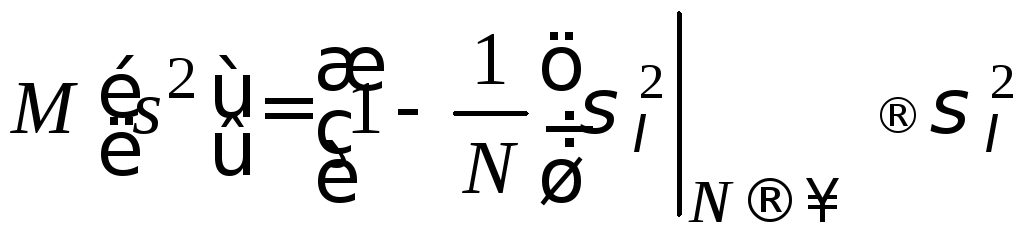 и оценка
и оценка![]() является, таким образом, асимптотически
несмещённой.
является, таким образом, асимптотически
несмещённой.
Пример
3. Случайная
величина
![]() принимает значения
принимает значения![]() и
и![]() с вероятностями
с вероятностями![]() и
и![]() ,
которые неизвестны:
,
которые неизвестны:
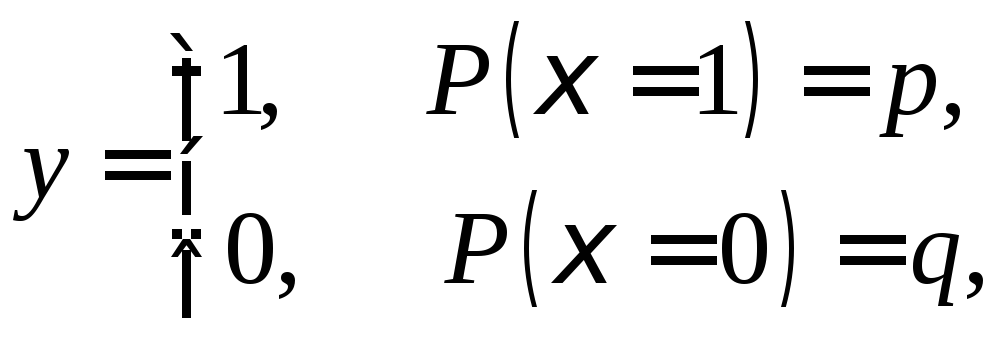 ,
,
![]() .
.
Проводится
![]() независимых экспериментов
независимых экспериментов![]() .
Необходимо оценить величину
.
Необходимо оценить величину![]() .
.
Положим,
в
![]() экспериментах появилось
экспериментах появилось![]() единиц и
единиц и![]() нулей. Вправе записать функцию
правдоподобия в виде:
нулей. Вправе записать функцию
правдоподобия в виде:
![]() .
.
Воспользуемся
критерием максимума правдоподобия для
оценки
![]() .
Приравнивая нулю производную по параметру
.
Приравнивая нулю производную по параметру![]() от логарифма функции правдоподобия,
получим оценку вероятности появления
единицы в эксперименте поN
измерениям
от логарифма функции правдоподобия,
получим оценку вероятности появления
единицы в эксперименте поN
измерениям
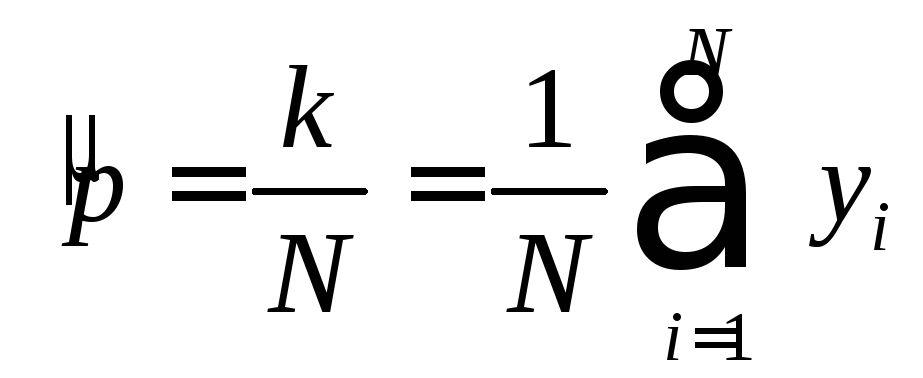 .
.
Вычислим
математическое ожидание и дисперсию
оценки
![]() :
:
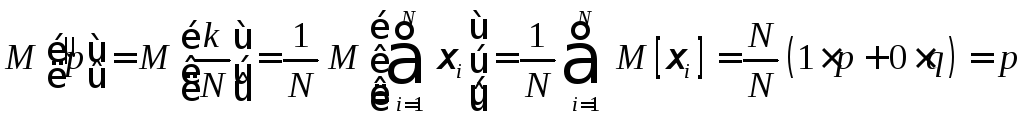 ,
,
что
доказывает отсутствия смещения оценки
![]() .
.
Дисперсия оценки имеет вид
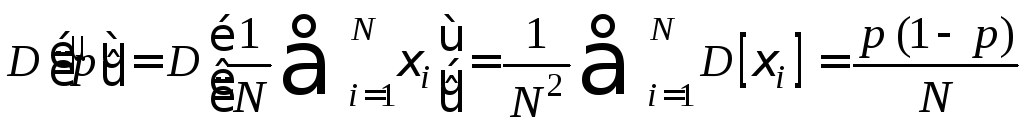 .
.
Докажем состоятельность оценки. Для этого вычислим абсолютное уклонение оценки от математического ожидания
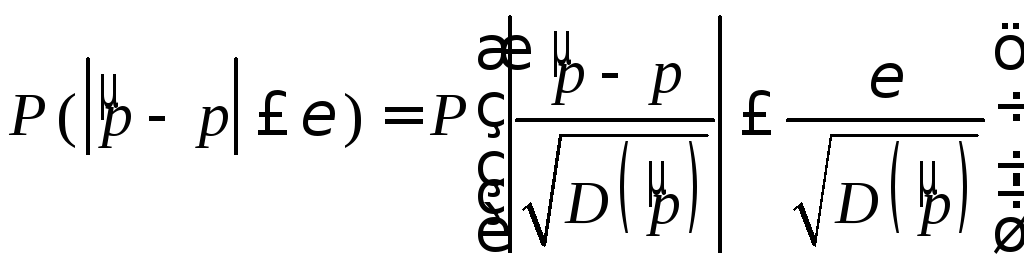 .
.
Известно,
что математическое ожидание и дисперсия
величины
![]() равны, соответственно, нулю и единице.
Подставим значение дисперсии в предыдущее
выражение и получим
равны, соответственно, нулю и единице.
Подставим значение дисперсии в предыдущее
выражение и получим
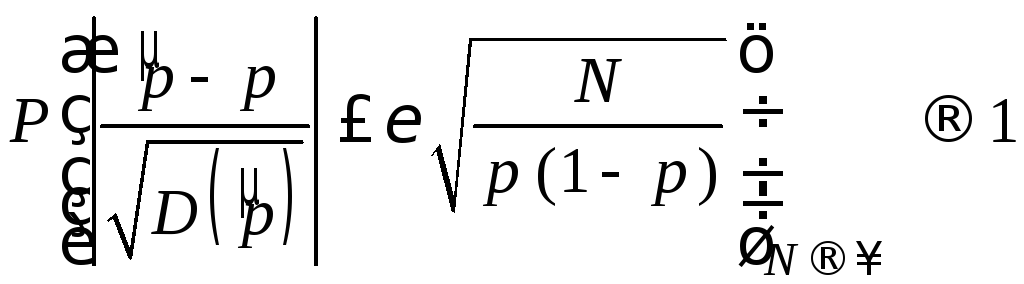 ,
,
что
доказывает состоятельность оценки
![]() .
.
Теперь
вычислим нижнюю границу дисперсии
![]() оценки
оценки![]() :
:
 .
.
Подставив
значение производной по параметру
![]() от логарифма функции правдоподобия в
знаменатель, получим
от логарифма функции правдоподобия в
знаменатель, получим
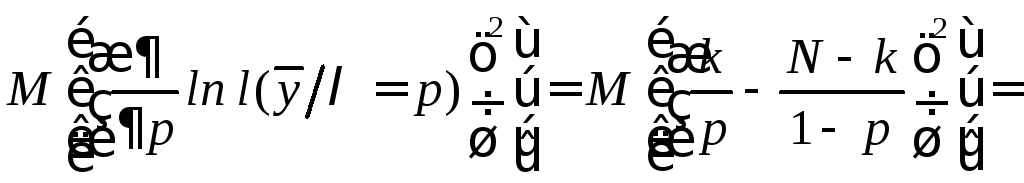

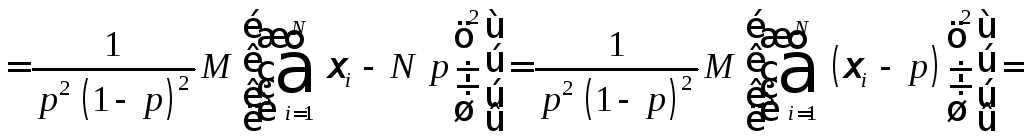
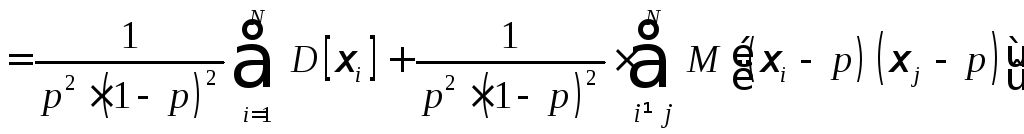 .
.
Но эксперименты независимы. Тогда имеем
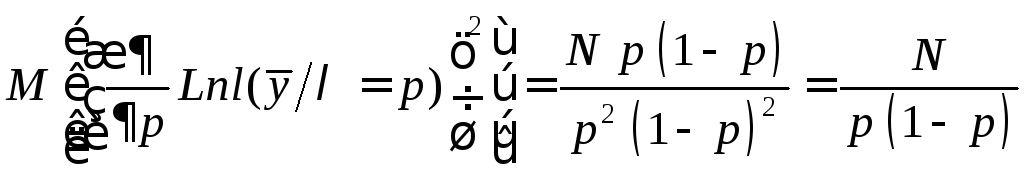 .
.
Подставив полученное выражение в неравенство Рао-Крамера, получим
![]() .
.
Как
видно, дисперсия оценки
![]() совпадает с нижней границей дисперсии.
Таким образом, оценка
совпадает с нижней границей дисперсии.
Таким образом, оценка![]() – эффективная.
– эффективная.
Дисперсия
оценки
![]() зависит от произведения
зависит от произведения![]() .
Максимум этого произведения достигается
при
.
Максимум этого произведения достигается
при![]() .
Используя это, заключаем, что дисперсия
оценки
.
Используя это, заключаем, что дисперсия
оценки![]() убывает с увеличением
убывает с увеличением![]() не медленнее, чем функция
не медленнее, чем функция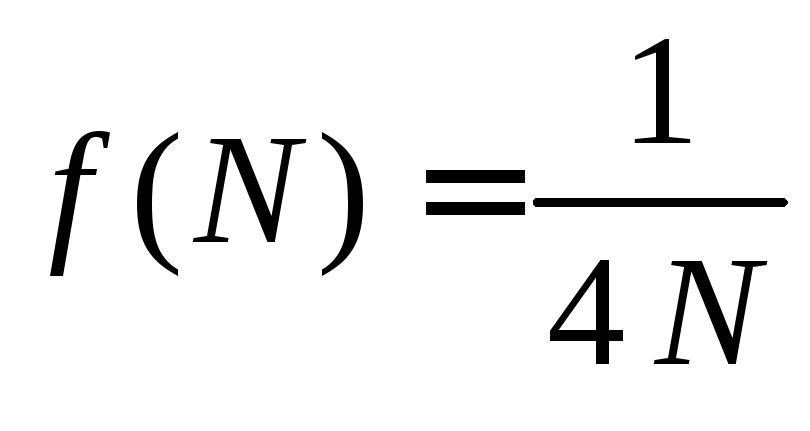 .
.
Статистика
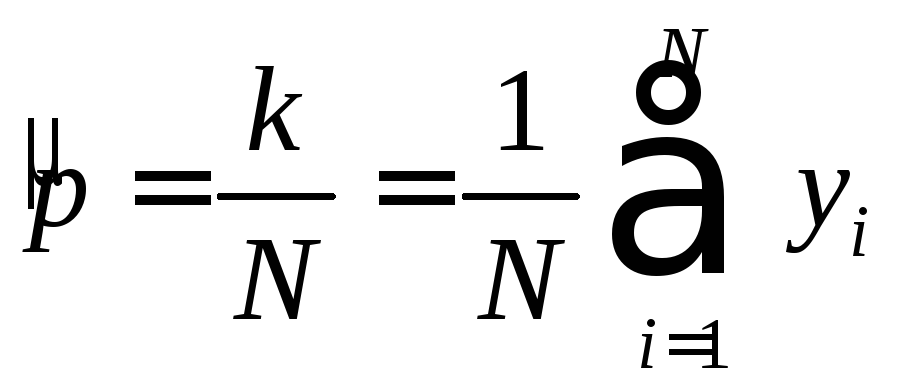 достаточна по определению, так как
достаточна по определению, так как
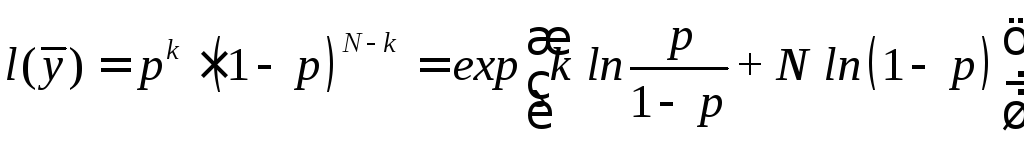 .
.
