
- •1. Введение
- •2. Типы решаемых задач
- •3. Проверка статистических гипотез
- •4. Критерии качества и правила принятия решений
- •4.1. Проверка двухальтернативных гипотез
- •4.1.1. Критерий Байеса
- •4.1.2. Минимаксный критерий
- •4.1.3. Критерий максимума апостериорной вероятности
- •4.1.4. Критерий максимума правдоподобия
- •4.1.5. Критерий Неймана-Пирсона
- •4.1.6. Последовательный критерий отношения вероятностей (Последовательный анализ Вальда)
- •4.1.7. Различение сигналов
- •5. Обработка непрерывных сигналов
- •5.1 Функционал правдоподобия
- •5.2 Применение функционала отношения правдоподобия для обнаружения полностью известного сигнала
- •5.3 Применение функционала отношения правдоподобия для обнаружения сигнала со случайной фазой
- •5.3.1. Расчет вероятностей ошибок
- •6. Оценка параметров сигнала
- •6.1. Свойства оценок параметров сигнала
- •6.2 Неравенство Рао-Крамера
- •7. Применение функционала отношения правдоподобия для оценки параметров сигнала
- •7.1. Оценка временного положения сигнала
- •7.2 Обработка пачки сигналов
- •7.3 Реализация алгоритма оценки временного положения сигнала
- •7.3.1 Корреляционный приёмник
- •7.3.2 Согласованный фильтр
- •Библиография
7. Применение функционала отношения правдоподобия для оценки параметров сигнала
В
предыдущей главе обсуждался вопрос
оценки параметров сигнала. В настоящей
главе рассмотрим проблему оценки
параметров сигнала по критерию максимума
функционала правдоподобия
![]() .
Однако, помня, что коэффициент
пропорциональности в функционале
правдоподобия зависит от корреляционной
матрицы и чтобы избежать неопределенности
при различных корреляционных матрицах,
используем критерий максимум функционала
отношения правдоподобия
.
Однако, помня, что коэффициент
пропорциональности в функционале
правдоподобия зависит от корреляционной
матрицы и чтобы избежать неопределенности
при различных корреляционных матрицах,
используем критерий максимум функционала
отношения правдоподобия
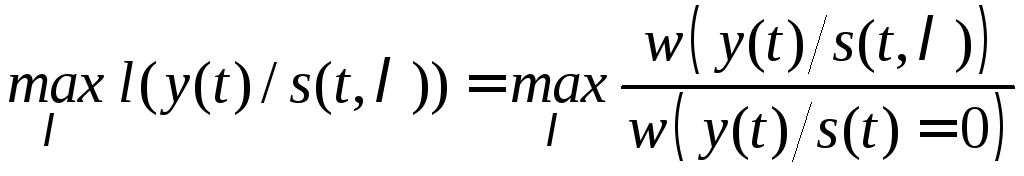 ,
(7.1)
,
(7.1)
так
же, как в задаче обнаружения сигнала.
Такое видоизменение критерия максимум
функционала правдоподобия не приведет
к изменению значения параметра
![]() ,
при котором функционал принимает
наибольшее значение, изменится только
само значение функционала.
,
при котором функционал принимает
наибольшее значение, изменится только
само значение функционала.
В явном виде выражение (7.1) будет
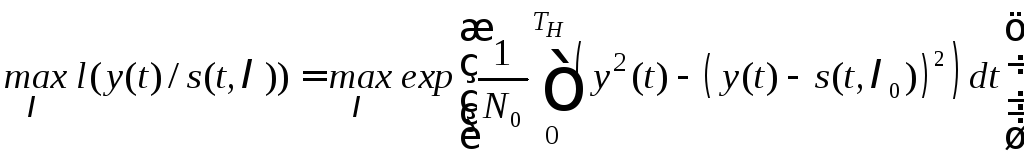 .
(7.2)
.
(7.2)
Вид
сигнала считается известным, но неизвестно
значение параметра
![]() ,
которое скрыто в реализации
,
которое скрыто в реализации![]() .
Более того, он может быть искажен шумом,
так как
.
Более того, он может быть искажен шумом,
так как![]() ,
где
,
где![]() – реализация нормального «белого» шума
с математическим ожиданием, равным
нулю, и спектральной плотностью мощности,
равной
– реализация нормального «белого» шума
с математическим ожиданием, равным
нулю, и спектральной плотностью мощности,
равной![]() ,
в интервале частот
,
в интервале частот![]() .
.
В
качестве параметра
![]() может выступать амплитуда, частота,
фаза, длительность задержки сигнала в
канале передачи и т.д. На приёмном конце
канала передачи информации необходимо
построить устройство, которое позволяет
оценивать этот параметр
может выступать амплитуда, частота,
фаза, длительность задержки сигнала в
канале передачи и т.д. На приёмном конце
канала передачи информации необходимо
построить устройство, которое позволяет
оценивать этот параметр![]() .
В этом устройстве используем информацию
о виде сигнала, т. е. генерируем сигнал
с переменным значением
.
В этом устройстве используем информацию
о виде сигнала, т. е. генерируем сигнал
с переменным значением![]() .
Будем изменять предполагаемый параметр,
назовём его
.
Будем изменять предполагаемый параметр,
назовём его![]() ,
в сигнале
,
в сигнале![]() .
Когда интеграл в выражении (7.2) примет
наибольшее значение при некотором
.
Когда интеграл в выражении (7.2) примет
наибольшее значение при некотором![]() ,
будем считать, оцениваемый параметр
,
будем считать, оцениваемый параметр![]() .
В дальнейшем реализуем эти положения
для конкретного параметра.
.
В дальнейшем реализуем эти положения
для конкретного параметра.
В силу того, что экспонента – монотонная функция своего аргумента, то достаточно (и удобнее) рассмотреть логарифм функционала отношения правдоподобия, то есть
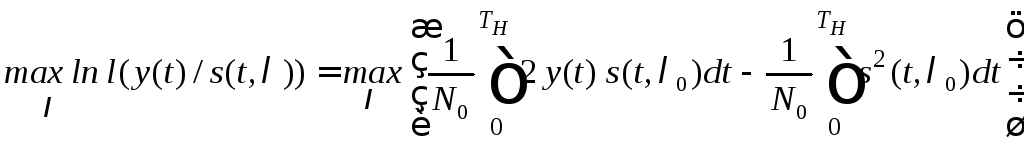 .
.
Если
параметр
![]() – не энергетический (задержка, фаза,
частота, но не амплитуда сигнала), то
второй интеграл не оказывает влияние
на положение точки максимума
– не энергетический (задержка, фаза,
частота, но не амплитуда сигнала), то
второй интеграл не оказывает влияние
на положение точки максимума![]() .
Следовательно, критерий максимум
функционала отношения правдоподобия
приобретает следующий вид:
.
Следовательно, критерий максимум
функционала отношения правдоподобия
приобретает следующий вид:
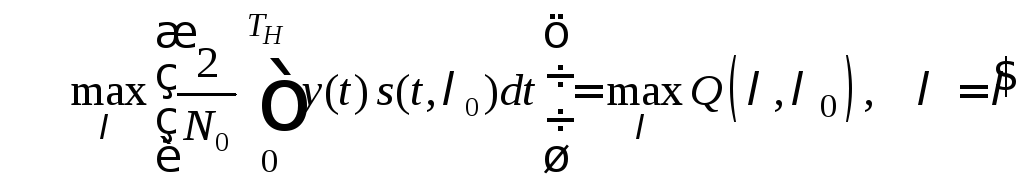 .
(7.3)
.
(7.3)
Далее
рассматривается
![]() как не энергетический параметр.
Корреляционный интеграл
как не энергетический параметр.
Корреляционный интеграл
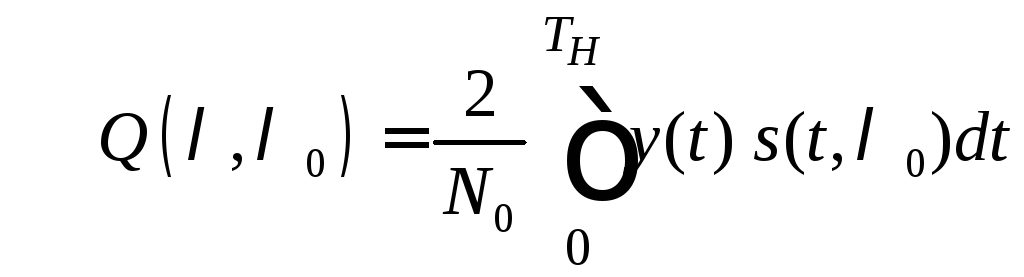 (7.4)
(7.4)
разбивается
на две части
![]() :
:
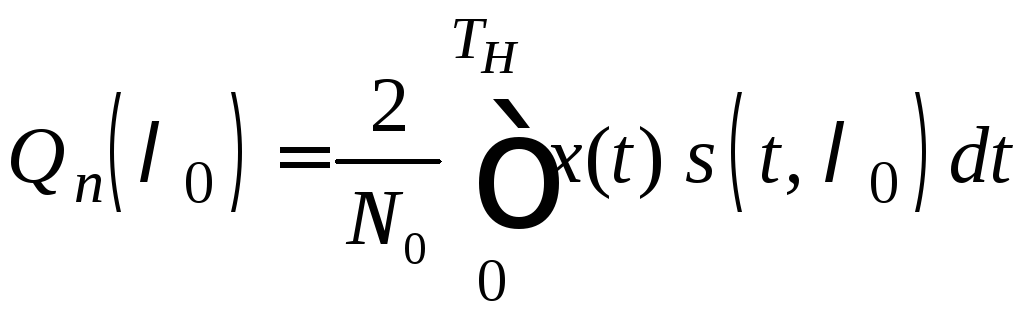 и
и
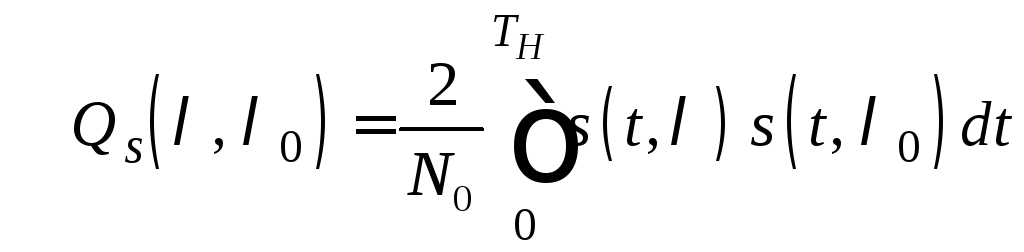 ,
(7.5)
,
(7.5)
где
![]() и
и![]() - соответственно шумовая и сигнальная
составляющие корреляционного интеграла
(7.4). Шумовая функция
- соответственно шумовая и сигнальная
составляющие корреляционного интеграла
(7.4). Шумовая функция![]() – случайная величина с математическим
ожиданием, равным нулю. Дисперсия
– случайная величина с математическим
ожиданием, равным нулю. Дисперсия![]() вычисляется как
вычисляется как
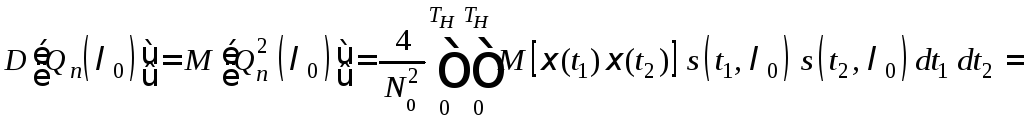
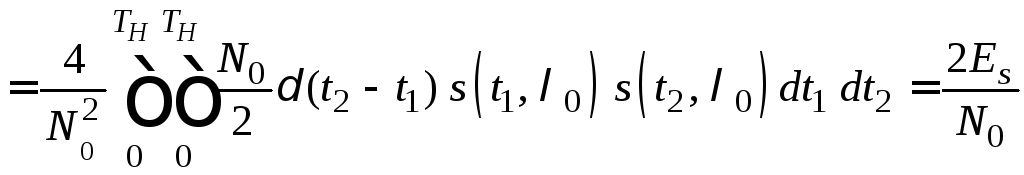 (7.6)
(7.6)
Сигнальная
функция
![]() - детерминированная величина и является
функцией переменной
- детерминированная величина и является
функцией переменной![]() :
:
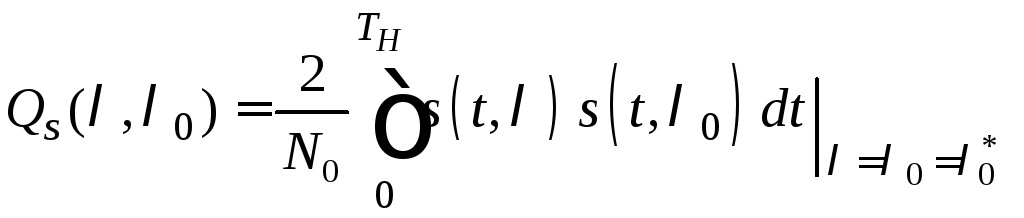 .
.
Используя неравенство Коши-Буняковского, получим
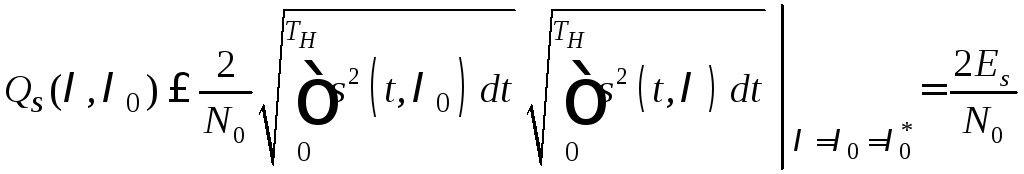 .
.
Знак
равенства будет лишь тогда, когда
![]() .
.
Рассмотрим математическое ожидание и дисперсию корреляционного интеграла:
![]()
![]() (7.7)
(7.7)
 (7.8)
(7.8)
Наибольшее
значение корреляционный интеграл
![]() достигает
при
достигает
при
![]() .
Эта точка максимума соответствует
оценке
.
Эта точка максимума соответствует
оценке![]() .
Но за счёт шумовой составляющей
.
Но за счёт шумовой составляющей![]() положение максимума относительно
истинного значения
положение максимума относительно
истинного значения![]() будет случайным. Рассчитать погрешность
оценки (дисперсию оценки параметра
будет случайным. Рассчитать погрешность
оценки (дисперсию оценки параметра![]() )
в общем случае довольно трудно. Поэтому
на практике для оценки нижней границы
дисперсии оценки
)
в общем случае довольно трудно. Поэтому
на практике для оценки нижней границы
дисперсии оценки![]() используют теоретически обоснованное
неравенство Рао-Крамера.
используют теоретически обоснованное
неравенство Рао-Крамера.
Помимо
дисперсии оценки
![]() качество обработки (оценки) принимаемого
сигнала характеризуетсяотношением
сигнал/шум
– отношение максимально-возможного
значения сигнальной составляющей
качество обработки (оценки) принимаемого
сигнала характеризуетсяотношением
сигнал/шум
– отношение максимально-возможного
значения сигнальной составляющей
![]() к среднеквадратичному значению шумовой
составляющей на выходе обрабатывающего
устройства:
к среднеквадратичному значению шумовой
составляющей на выходе обрабатывающего
устройства:
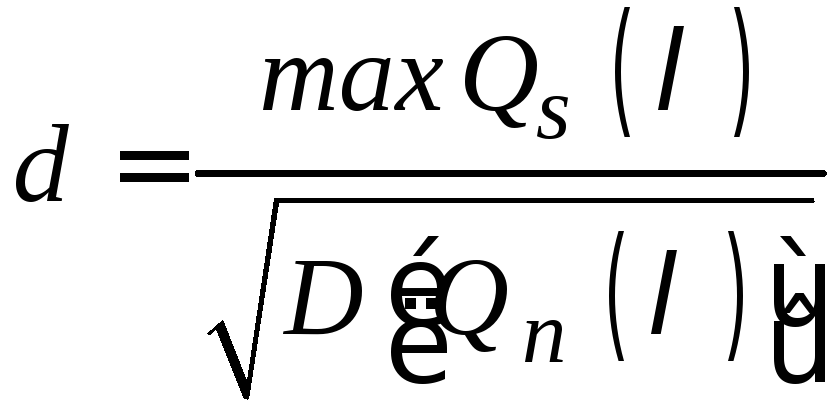 (7.9)
(7.9)
Для не энергетического параметра сигнала критерий максимума функционала отношения правдоподобия позволяет вычислить отношение сигнал/шум
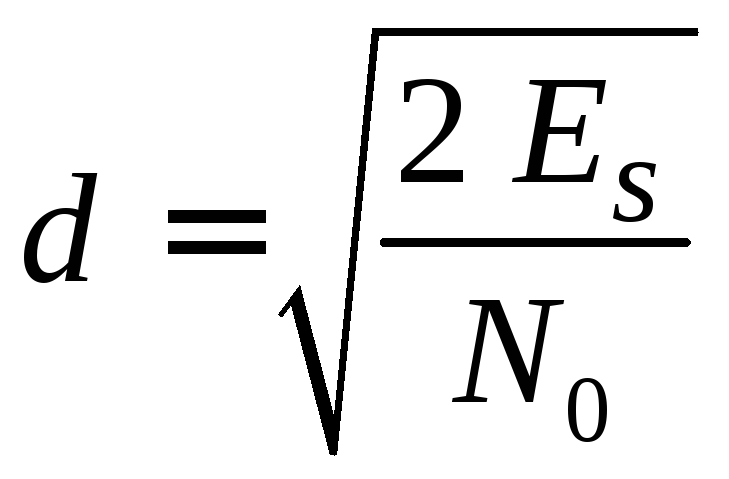 (7.10)
(7.10)
