
- •Механика Лекция 1
- •Ускорение
- •Поступательное и вращательное движения твёрдого тела
- •Преобразования Галилея
- •Основное уравнение динамики
- •Центр масс.
- •Движение тела переменной массы
- •Лекция 3 Закон сохранения момента импульса
- •Основной закон динамики вращательного движения
- •Лекция 4 Работа. Энергия. Закон сохранения энергии в механике
- •Консервативные силы
- •Потенциальная энергия
- •Сопоставление формул механики поступательного движения и вращения вокруг неподвижной оси
- •Лекция 5 Колебания
- •Свободные незатухающие колебания
- •Лекция 6 Свободные затухающие колебания
- •Вынужденные колебания
- •Резонанс
- •Лекция 7 Механические волны
- •Энергия волны
- •Интерференция волн
- •Стоячие волны
- •Лекции 8 и 9 Элементы релятивистской механики
- •Преобразования Лоренца
- •1). Одновременность событий в разных системах отсчёта
- •2). Длина тел в разных системах
- •3). Промежуток времени между событиями
- •Интервал
- •Преобразование скоростей
- •Элементы релятивистской динамики
- •Закон взаимосвязи массы и энергии
- •Связь между энергией и импульсом релятивистской частицы
Сопоставление формул механики поступательного движения и вращения вокруг неподвижной оси
|
Поступательное движение |
Вращение |
|
|
|
|
|
|
|
т – масса |
J – момент инерции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 5 Колебания
Колебаниями называют процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени.
Колебания называют периодическими если значения всех физических величин, характеризующих колебательную систему и изменяющихся при её колебаниях, повторяются через равные промежутки времени.
Т0 – период колебаний (наименьший промежуток времени, удовлетворяющий этому условию);
![]() –частота колебаний;
–частота колебаний;
![]() –циклическая
(круговая) частота (в электротехнике
–циклическая
(круговая) частота (в электротехнике
![]() называют угловой частотой).
называют угловой частотой).
Гармоническими
называют периодические колебания
величины
![]() ,
если
,
если
![]() или
или
![]() где
где
![]()
![]() –амплитуда
колебаний;
–амплитуда
колебаний;
![]() –фаза колебаний;
–фаза колебаний;
![]() –начальная фаза
колебаний
–начальная фаза
колебаний
![]()
Первая и вторая
производные по времени от гармонически
колеблющейся величины
![]() также совершают гармонические колебания
той же частоты:
также совершают гармонические колебания
той же частоты:
![]()
![]()
Амплитуды
![]() и
и![]() соответственно равны
соответственно равны![]() и
и![]() .
.
Разность фаз
колебаний
![]() иS
постоянна
и равна
иS
постоянна
и равна
![]() (величина
(величина![]() опережаетS
по фазе на
опережаетS
по фазе на
![]() ).
).
Величина
![]() опережаетS
по фазе на
опережаетS
по фазе на
![]() .
.
Сравнивая значения
S
и
![]() видно, что гармонически колеблющаяся
величина удовлетворяет дифференциальному
уравнению
видно, что гармонически колеблющаяся
величина удовлетворяет дифференциальному
уравнению
![]() .
.
Общее решение этого уравнения:
![]() , где
, где
А1 и А2 – произвольные постоянные интегрирования, определяемые из начальных условий
![]() .
.
Общее решение можно привести к виду
![]() , где
, где
![]() и
и
![]() .
.
Физическая величина S совершает гармонические колебания в том и только в том случае, если она удовлетворяет дифференциальному уравнению гармонических колебаний
![]() , где
, где
![]() .
.
Векторная диаграмма. Гармонические колебания можно изобразить графически с помощью вращающегося вектора на плоскости, модуль которого равен амплитуде А колебаний.
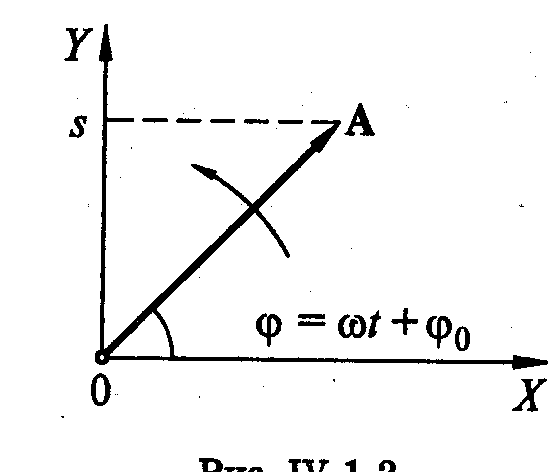
Вектор А
равномерно
вращается вокруг точки О с угловой
скоростью
![]() ,
равной циклической частоте
,
равной циклической частоте
![]() .
.
Сложение гармонических колебаний.
а) сложение колебаний одного направления
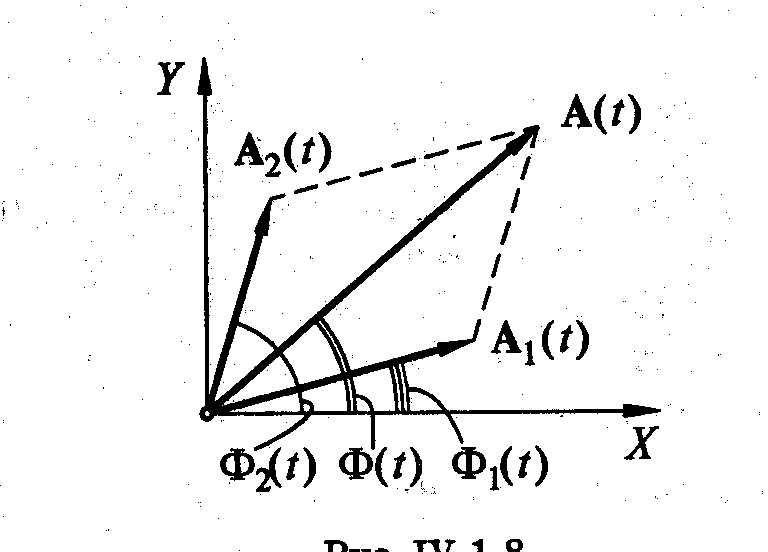
![]()
![]()
![]()
По теореме косинусов
![]() , где
, где
![]() и
и
![]()
![]() .
.
Негармонические
колебания,
получающиеся в результате наложения
двух одинаково направленных гармонических
колебаний с близкими частотами
![]() ,
называютбиениями.
,
называютбиениями.
Пусть
![]() и
и
![]() ,
где
,
где
![]() .
.
Тогда
![]() , где
, где
![]()
![]()
В частности, если А1= А2 = А0 , то
![]() и
и
![]() так. что
так. что
![]() .
.
П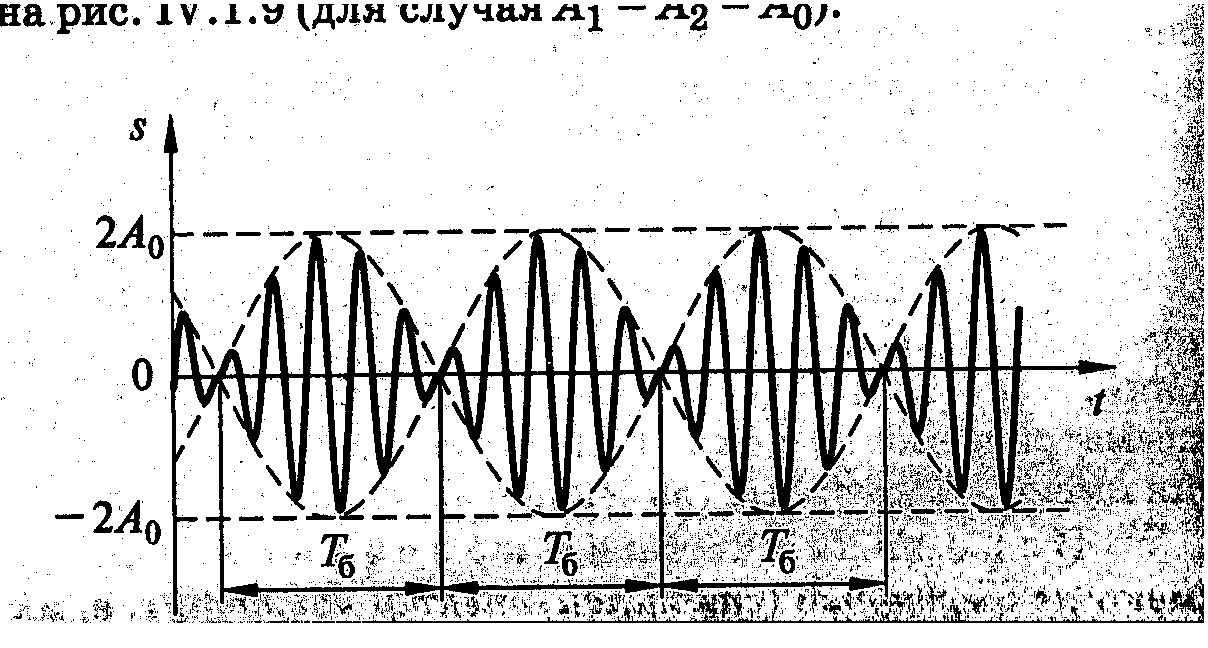 ериод
биений –
ериод
биений –![]()
Частота биений
–
![]()
![]()
Любое сложное
периодическое колебание
![]() можно представить в виде суммы простых
гармонических колебаний с циклическими
частотами, кратнымиосновной
циклической частоте
можно представить в виде суммы простых
гармонических колебаний с циклическими
частотами, кратнымиосновной
циклической частоте
![]()
![]()
Такое представление
периодической функции
![]() называютразложением
её в ряд
Фурье или
гармоническим
анализом сложного периодического
колебания.
называютразложением
её в ряд
Фурье или
гармоническим
анализом сложного периодического
колебания.
б) сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.
Пусть точка М одновременно колеблется вдоль осей координат ОХ и ОУ по законам:
![]() и
и
![]()
Для получения уравнения траектории надо избавиться от t .
![]() и
и
![]()
Тогда
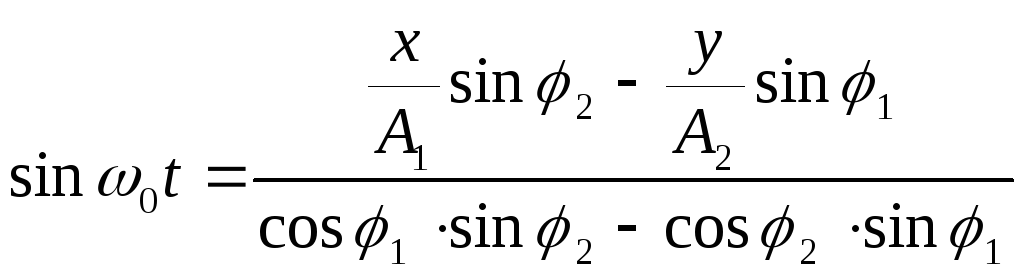
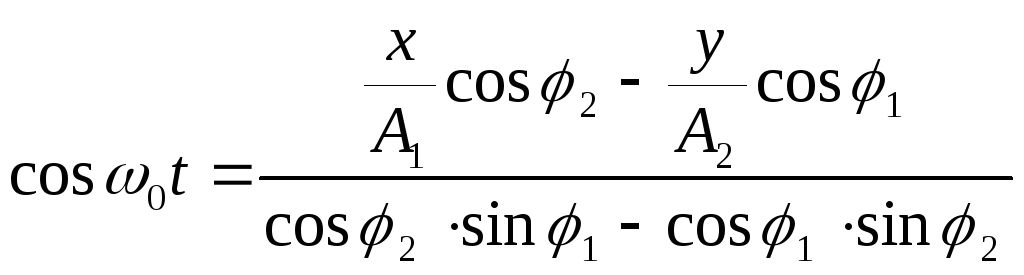
Так как
![]() , получаем
, получаем

или
![]() .
.
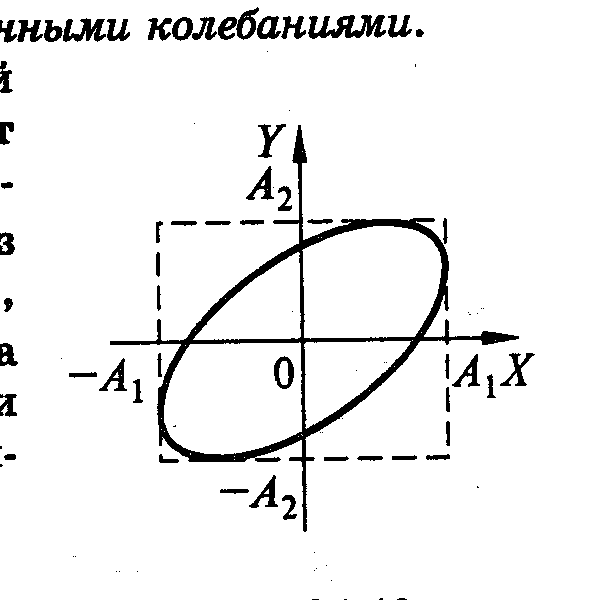
Траектория имеет
форму эллипса, который колеблющаяся
точка М проходит за время одного периода
![]() .
.
Если
![]() ,
гдет
= 0; +1; -1; +2; -2; … , то оси эллипса совпадают
с осями ОХ и ОУ, а размеры его полуосей
равны А1
и А2
,
гдет
= 0; +1; -1; +2; -2; … , то оси эллипса совпадают
с осями ОХ и ОУ, а размеры его полуосей
равны А1
и А2
![]() .
.
Если при этом А1 = А2 , то траектория точки М – окружность.
При
![]() эллипс вырождается в отрезок прямой.
эллипс вырождается в отрезок прямой.
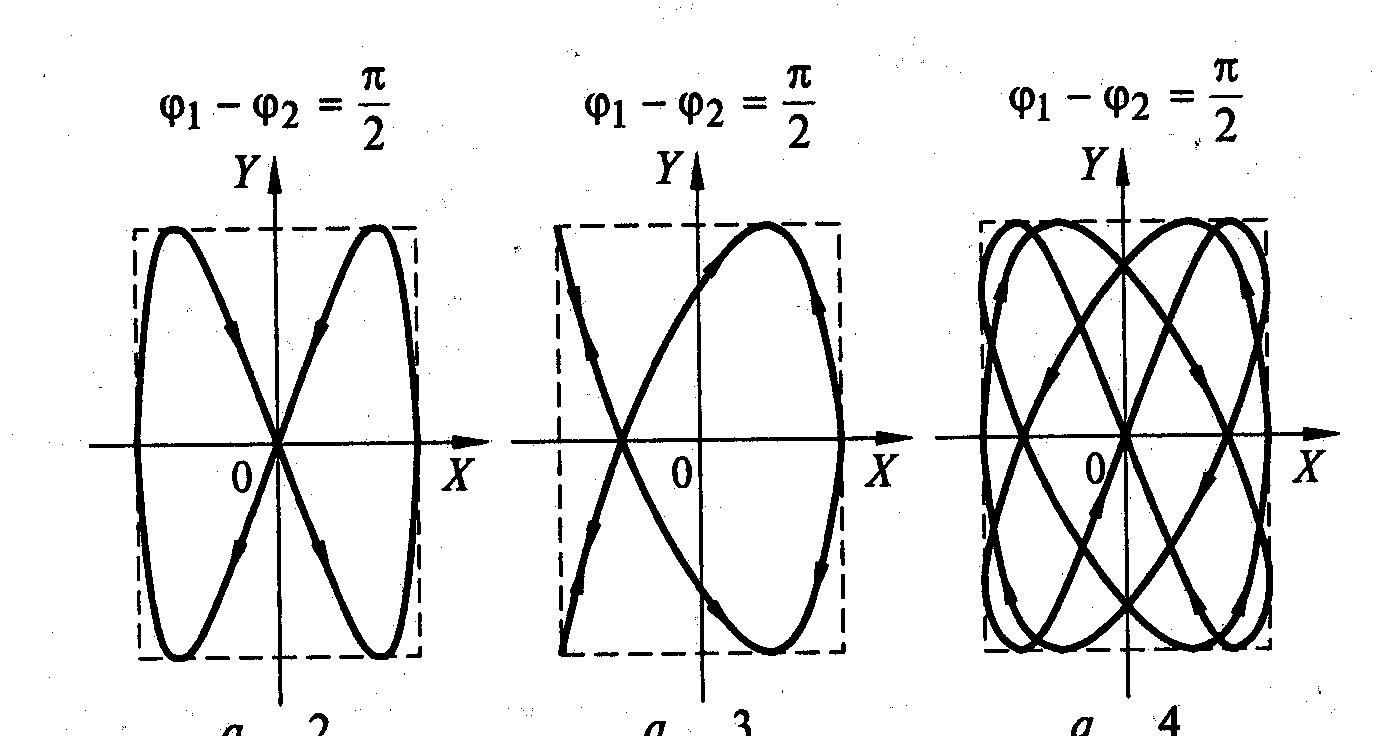
в) сложение взаимно перпендикулярных колебаний кратных частот:
![]() и
и
![]()
п1 и п2 – целые числа
точка М имеет траекторию в виде замкнутой кривой, называемой фигурой Лиссажу , зависящую от соотношения амплитуд, частот и начальных фаз складываемых колебаний.
![]()
![]()
![]()
