3.2.5. Отражение звука неровной поверхностью

Рассмотренный выше случай рассеяния плоских волн на плоских границах раздела разнородных сред на практике может применяться далеко не всегда. Достаточно часто приходиться встречаться с отражением упругих волн от поверхностей, отличающихся различной степенью неровности (шероховатых). Задача рассеяния звука на такой поверхности встречается, например, при расчете потерь энергии при отражении от взволнованной поверхности моря, от неровностей грунта, а также от шероховатой поверхности при неразрушающем контроле в промышленности и медицинских исследованиях.

При отражении звука от шероховатых поверхностей наряду с зеркально отраженной волной возникают и компоненты рассеяния в других направлениях, определяемых соотношениями длины волны и параметров поверхностей.

Сравнительно простые результаты этой, в общем случае сложной, задачи могут быть получены при выполнении определенных условий, накладываемых на свойства поверхности (рис. 3.10):

1.Средняя высота (амплитуда) шероховатостей много меньше длины волны звука (диффузное рассеяние);

2. Протяженность неровностей вдоль поверхности и их радиуса должно быть много больше длины волны звука ().

Количественный критерий для описания условий рассеяния определяется параметром Рэлея: , где- волновое число,- средняя высота неровностей,- угол падения плоской волны. Для диффузного рассеяния1.

Для проведения аналитического решения о рассеянии звука на шероховатой поверхности при <<1 можно разложить функции, участвующие в записи граничных условий, заданных на неровной поверхности, в ряд Тейлора относительно плоской поверхности по малому параметру . При использовании метода малых возмущений можно свести решение задачи к решению системы волновых уравнений для компонент различного порядка малости по параметру, причем граничные условия для каждого последующего приближения получается на основе решения для предыдущего приближения.

Для плоской задачи ограничимся рассмотрением волнового процесса в окрестности периодически шероховатой (волнистой) поверхности в плоскости xoz:

, (3.43)

Решение волнового уравнения (3.43) ищется при граничных условиях для каждого приближения номера :

, (3.44)

где - решение дляn-ого приближения ( порядка ); ; - период неровной «косинусоидальной» поверхности.

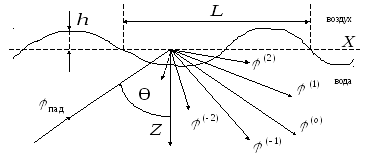
Рис. 3.10

Решение для произвольного приближения имеет вид: (при этом временной множитель учитывать не будем):

, (3.45)

где .

Таким образом, при , кроме зеркально отраженной волныобразуется система дифракционных «пучков» - угловых спектров с амплитудами, спадающими по закону. При учете энергии, уносимой только волной «нулевого спектра», коэффициент отражения от неровной поверхности определяется выражением. Именно образование «дифракционных» пучков-спектров и является причиной диффузного рассеяния. Один из этих «спектров» может совпасть с падающей волной, образуяобратно отраженную волну [6-8].

3.2.6. Отражение звука искривленной поверхностью. Интеграл Кирхгофа

Как уже говорилось ранее при расчете звуковых полей, излучаемых колеблющимися поверхностями, возникает необходимость вычисления потенциала поля в некоторой области пространства по значению потенциала и его нормальной производной (т.е. по значению звукового давления и колебательной скорости) на заданной поверхности. Рассмотрим произвольную область, ограниченную поверхностьюS, представленную на рис 3.11.

Рис. 3.11

Требуется найти связь между значением в некоторой области пространстваV для точки наблюдения (.) М и значением Ф на поверхности S. Такая связь может быть получена путем использования формулы Грина, связывающей значения объемного и поверхностного интегралов.

Формула Грина записывается следующим образом: любые две функции и, непрерывны вместе со своими первыми и вторыми производными в объемеV, удовлетворяют соотношению.

. (3.46)

В этой формуле n – внешняя нормаль. Пусть внутри объема V существует два звуковых поля, описываемых функциями и, которые удовлетворяют уравнению Гельмгольца:

. (3.47)

Звуковое поле – это основное поле, которое требуется определить; полеявляется вспомогательной величиной. Звуковое полев уравнении Гельмгольца (3. ) умножим на, а второе уравнение - на, затем вычтем второе уравнение из первого и сумму проинтегрируем по объемуV.

В результате получим соотношения:

. (3.48)

Применяя к последнему выражению формулу Грина, можно записать:

. (3.49)

Вспомогательной функцией может быть любая функция, удовлетворяющая уравнению Гельмгольца и сформулированным выше требованиям непрерывности в объемеV. Выберем в качестве поле точечного ненаправленного источника, помещенного в точке наблюдения М.

(3.50)

где ,- радиус вектор, проведенный от начала координат в точку наблюдения М;- радиус вектор, направленный в любую точку поля.

В сферической системе координат в силу симметрии задачи уравнение Гельмгольца можно записать в виде:

. (3.51)

Прямой подстановкой легко установить, что функция удовлетворит этому уравнению.

Это утверждение справедливо для всех точек области V, за исключением точки . В точкефункция имеет особенность, и дифференцировать ее в этой точке невозможно. Кроме того, для функцииневерна и формула Грина, т.к. она справедлива лишь для функций, непрерывных во всех точках области. Поэтому точку наблюдения надо исключить из рассматриваемой области. Для этого окружим точку М малой сферойрадиусаа. Новая область будет расположена между и, аполная новая поверхность, ограничивающая объем, будет состоять из двух частей и.

Рассмотрим интеграл по поверхности . Наружная к области нормаль к поверхностибудет направлена внутрь сферы. Из-за этого наимеем. Сколь бы малым ни выбиралось значение радиуса окружности - а, величины ина поверхности будут оставаться конечными, так что применение формулы Грина является допустимым.

Вычислим:

. (3.52)

Поскольку искомое поле является непрерывной функцией координат в любой точке области, то в пределах малой сферы радиуса а, можно считать, что имало зависит от положения точки на поверхности. Поэтомуиможно вынести из под знака интеграла, заменив их значения в точке, определенной вектором. Для функцииэтого сделать нельзя, так как внутриона обладает особенностью.

В результате можно записать:

.

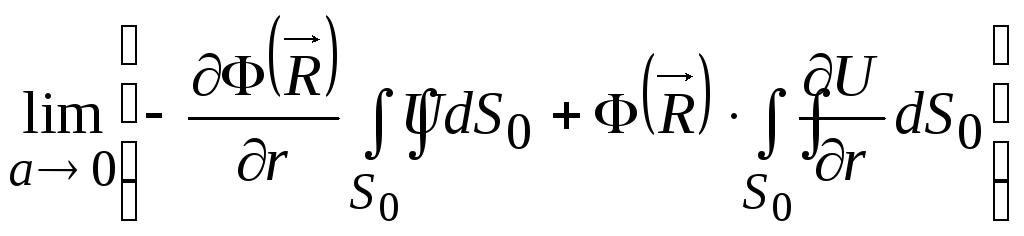Учитывая, что на поверхности :

,

где – элемент телесного угла, получим:

.

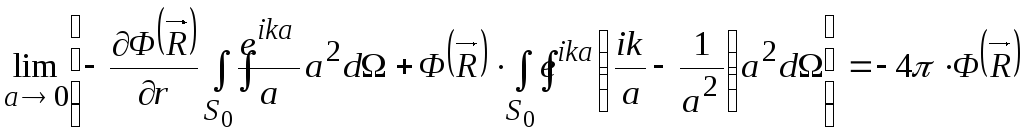Отметим, что поверхность интегрирования является суммой S и . Тогда получим, что, откуда:

. (3.53)

Так как интегрирование проводится по поверхности , то величиныв этой формуле являются расстоянием от точки наблюденияМ до элемента поверхностиS.

Полученное выражение (3.53) носит название формулы Кирхгофа или интеграла Кирхгофа.

Использование полученной формулы для практических расчетов тоже затрудняется тем обстоятельством, что на излучающей поверхности обычно известна одна из величин и. Если колебательная скорость(или) на поверхности задана, то звуковое давление пропорциональное потенциалу Ф, как правило, оказывается неизвестным. Поэтому неизвестная величина будет входить и в левую и в правую части уравнения (3.53). Фактически формула (3.53) и является интегральным уравнением. В ряде случаев удается из физических соображений указать хотя бы приближенную связь между величинами Ф и.

Тогда интеграл Кирхгофа определяет приближенное решение задачи излучения им дифракции звука. Если поверхность S представляет собой плоскость, то интеграл Кирхгофа удается свести к формулам, которые дают точные решения для случаев, когда на поверхности оказывается известной лишь одна из величин Ф и . Такие формулы называются интегральными формулами Гюйгенса.

Рассмотрим излучение бесконечной плоскости S в верхнее полупространство. Дополним плоскость до замкнутой поверхности полусферой(рис. 3.12).

При увеличении радиуса полусферы интеграл по должен стремиться к нулю в силу принципаизлучения. Поэтому при использовании формулы Грина можно ограничиться интегрированием по плоскости. Запишем формулу интеграла Кирхгофа в виде.

. (3.54)

где U – вспомогательная функция, представляющая собой поле точечного источника. Выберем в (3.54) в качестве U функцию, которая описывает поле точечного источника, расположенного над абсолютно жесткой поверхностью.

Рис. 3.12

Очевидно, что в точке М поле от источника, помещенного в произвольную точку над плоскостью может быть представлено в виде суммы полей источника и зеркально расположенного источника:

. (3.55)

Нормальная производная этого поля определяется выражением:

. (3.56)

Устремим точку Q к границе. Учитывая, что на границе ,, получим. Подставляя эти значения (3.55, 3.56) в формулу (3.54), получим:

. (3.57)

Выражение (3.57) называется первой интегральной формулой Гюйгенса. Важным преимуществом этой формулы по сравнению с интегралом Кирхгофа является то, что здесь для расчета звукового поля во всем полупространстве требуется знать только одну величину , т.е. колебательную скорость поверхности. Перейдем от потенциалов к колебательной скорости и звуковому давлению:;. Тогда:

(3.58)

Полученное выражение (3.57) служит основной формулой для расчета звуковых полей плоских излучателей и приемников звука. Формально эти выражения являются точными, однако при их применении колебательная скорость должна быть известна на всей поверхности S. Реальные излучающие поверхности ограничены, поэтому при расчете звуковых полей плоских излучателей их излучающая поверхность дополняется абсолютно жестким экраном, на котором можно положить .

Для того, чтобы получить вторую интегральную формулу Гюйгенса, следует в качестве вспомогательной функции выбрать поле точечного, ненаправленного источника, расположенного над абсолютно мягкой поверхностью. В этом случае поле мнимого источника будет противоположно по знаку полю источника:

. (3.59)

Вычислив производную от (3.59) и устремив точкуQ к границе, получаем: . Тогда:

. (3.60)

Вместо потенциалов в (3.60), по аналогии с (3.58) легко перейти к звуковым давлениям.

Это выражение (3.60) и есть вторая интегральная формула Гюйгенса, определяющая значения звукового давления в полупространстве по известной величине звукового давления на плоскости.

Как и ранее, для ограниченных участков плоскости, излучатель конечных размеров следует дополнить до бесконечной плоскости «абсолютно мягким экраном», на котором можно задать условие Ф = 0. Тогда интегрирование нужно проводить только по поверхности излучателя.