- •Математический анализ
- •4 Семестр
- •Содержание.
- •Лекция № 1. Теория функций комплексного переменного. Комплексные числа и действия над ними.
- •10. Определение. Свойства.
- •20. Комплексная плоскость с и декартова плоскость .
- •30. Тригонометрическая форма комплексных чисел.
- •20. Предел f(z) в точке. Непрерывность.
- •30. Производная f(z). Условия Коши-Римана.
- •40. Теорема Коши-Римана.
- •Лекция № 3.
- •10. Геометрический смысл аргумента и модуля .
- •Некоторые конформные отображения.
- •10. Линейное отображение.
- •Лекция № 4.
- •Дробно-линейные отображения.
- •30. Определение. Простейшие свойства.
- •50. Декомпозиция дробно-линейного отображения.
- •Лекция № 5.
- •Лекция № 6.
- •20. Общий вид дробно-линейного отображения.
- •Лекция № 7. Интегрирование функций комплексного переменного.
- •10. Определение
- •Лекция № 8. Формула коши.
- •10. Окончание предыдущей лекции.
- •Лекция № 9. Следствия из формулы коши.
- •10. Напоминание.
- •30. Следствие3 (Теорема Лиувилля)
- •Комплексные ряды.
- •Лекция № 10. Степенные ряды. Ряды тейлора.
- •Лекция № 11.
- •Лекция № 12. Особые тчоки аналитических функций.
- •10. Несколько замечаний к разложению Лорана.
- •30. Классификация изолированных особых точек.
- •Лекция № 13.
- •Лекция № 14.
- •Лекция № 15.
- •Лекция № 16. Интегралы пуассона.
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Лекции
Математический анализ
4 Семестр
Лектор Дубинский Юлий Андреевич
Москва, 2009/2010
Содержание.
|
Лекция № 1.
|
Теория функций комплексного перемеенного. Комплексные числа и действия над ними........................................................................................... 4 |
|
Лекция № 2. |
Функции комплексного переменного............................................................9 |
Лекция № 1. Теория функций комплексного переменного. Комплексные числа и действия над ними.
10. Определение. Свойства.
Определение 1.
Комплексными
числами назовём символы
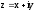 ,
где
,
где и
и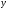 – вещественные числа,
– вещественные числа, – мнимая единица.
– мнимая единица.
Принято
 называть вещественной частью, а
называть вещественной частью, а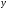 – мнимой.
– мнимой.

Определение 2.
Алгебраически множество данных символов будут образовывать поле комплексных чисел, если будут определены операции сложения, вычитания, умножения и деления.
Определение 3.
Комплексно
сопряженным с число
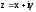 назовём символ
назовём символ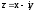 .
.
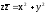
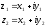
сложение комплексных чисел
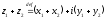
вычитание комплексных чисел
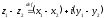
умножение комплексных чисел
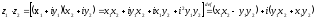
деление комплексных чисел
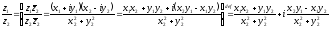
Замечание.
Не
трудно проверить, что
 –
умножение коммутативно.
–
умножение коммутативно.
Также выполняются свойства коммутативности и дистрибутивности сложения.
Вывод: поле комплексных чисел является расширением поля вещественных чисел с сохранением всех свойств 4-x арифметических операций.
Пример.
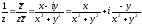
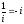
20. Комплексная плоскость с и декартова плоскость .
Очевидно,
что
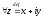 соответствует пара вещественных чисел
соответствует пара вещественных чисел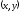 ,
которая определяет точку на
,
которая определяет точку на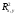 и наоборот – каждой точке
и наоборот – каждой точке
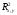 соответствует комплексное число
соответствует комплексное число .
При этом должное соответствие взаимно
однозначно, поэтому множество комплексных
чисел называют комплексной плоскостью
и на практике часто геометрически
отождествляют с
.
При этом должное соответствие взаимно
однозначно, поэтому множество комплексных
чисел называют комплексной плоскостью
и на практике часто геометрически
отождествляют с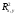 .
.
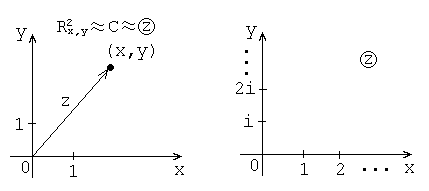
Это совмещение особенно полезно при изучении геометрических вопросов как теории комплексных чисел, так и теории комплексных функций.
Замечание.
Трактовка комплексных чисел как векторов декартовой плоскости даёт геометрическую иллюстрацию сложения и вычитания комплексных чисел (обычное сложение и вычитание векторов).

Геометрическая иллюстрация операций умножения и деления связана с тригонометрической или экспоненциальной формой записи комплексного числа.
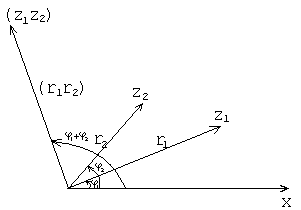
30. Тригонометрическая форма комплексных чисел.
Рассмотрим на декартовой плоскости полярную систему координат:
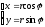
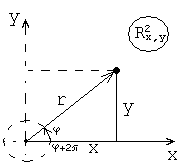
Утверждение 1.
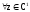 записывается
в виде
записывается
в виде
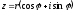 .
.
Определение 4.
Число
 называется модулем комплексного числа
и обозначается
называется модулем комплексного числа
и обозначается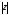 .
.
Определение 5.
Значение
(угол)
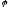 называется аргументом и обозначается
символом
называется аргументом и обозначается
символом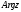 .
Заметим, что
.
Заметим, что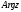 определяется не однозначно на
определяется не однозначно на .
Очевидно, годится любой угол
.
Очевидно, годится любой угол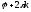 .
.
Определение 6.
Во
избежание путаницы выделяется главная
ветвь аргумента
 ,
которая обозначается
,
которая обозначается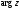 .
.
Утверждение 2.
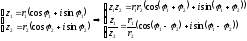
40. Экспоненциальная форма комплексного числа.
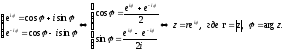
Тогда
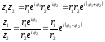
В этой записи также легко записать формулы Муавра:
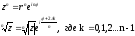
Лекция № 2.
Замечание.
Укажем
пропущенную на предыдущей лекции
зависимость
 от вещественных переменных х, у:
от вещественных переменных х, у:
(*)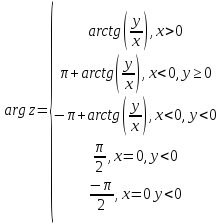
Формула
(*) соответствует определению
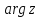 с разрезом плоскости С по отрицательной
полуоси ОХ.
с разрезом плоскости С по отрицательной
полуоси ОХ.
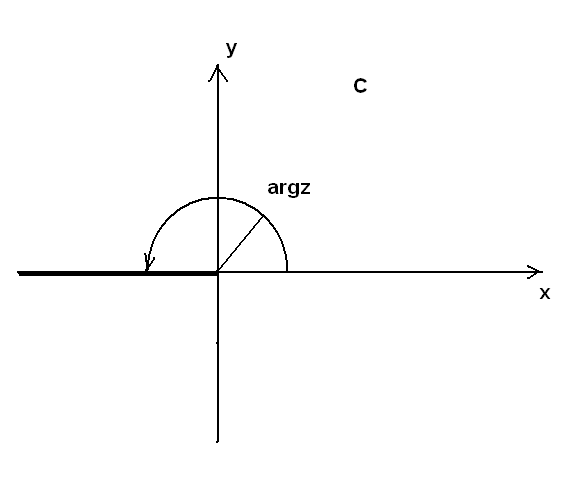

При
этом значения
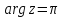 придает верхнему «берегу» разреза.
Аналогично можно выписать формулы при
разрезе вдоль положительной полуоси
ОХ. При этом
придает верхнему «берегу» разреза.
Аналогично можно выписать формулы при
разрезе вдоль положительной полуоси
ОХ. При этом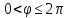
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.
10. Определение. Примеры.
Пусть
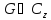 – комплексная область на плоскости
– комплексная область на плоскости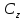 .
Пусть
.
Пусть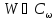 –
некоторая область на плоскости
–
некоторая область на плоскости
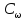 ,
,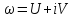 .
.
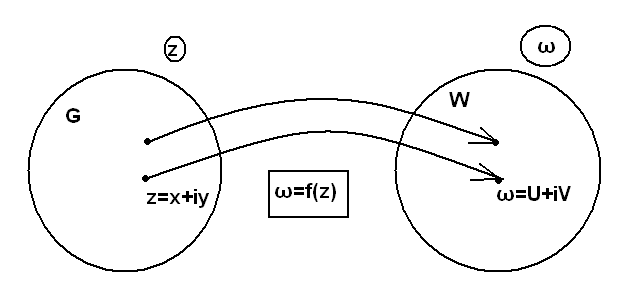
Определение 1.
Всякое
отображение области G
на области W
называется функцией комплексного
переменного
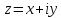 со значениями
со значениями в областиW.
в областиW.
Заметим,
что при заданной функции
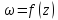
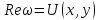 –функция
вещественных (х, у),
–функция
вещественных (х, у),
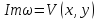 –функция
вещественных (х, у).
–функция
вещественных (х, у).
Таким образом, всякая комплексная функция однозначно определяется двумя вещественными функциями:
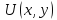 –реальная
(действительная) часть функции
–реальная
(действительная) часть функции
 –мнимая
часть функции
–мнимая
часть функции
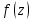
Поэтому,
говоря о комплексной
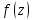 ,
указывают, что
,
указывают, что .
.
Примеры.
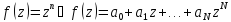 ,
где
,
где
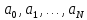 – комплексные числа, аN
– целое.
– комплексные числа, аN
– целое.