Тема 6. Линейные цепи при гармоническом

ВОЗДЕЙСТВИИ. РАСЧЕТ ЧАСТОТНЫХ ХАРАКТЕРИСТИК

6.1. Расчет мгновенного значения напряжения или тока

Расчеты мгновенных значений напряжений и токов (откликов) в цепях при гармоническом воздействии проводят методом комплексных амплитуд (символическим методом).

Суть этого метода в том, что сначала рассчитывают комплексную амплитуду отклика в показательной форме, например, напряжения

(6.1)

Затем, записывают мгновенное комплексное значение отклика (6.2) в тригонометрической форме путем умножения комплексной амплитуды на оператор вращения e^jωt

(6.2)

Мгновенное значение отклика u(t) (6.3) является реальной частью мгновенного комплексного значения (6.2)

(6.3)

Пример 6.1. Рассчитать мгновенное значение тока в контуре (рис. 6.1), если включен источник гармонического напряжения e(t) = Ecos(ωt+φ₀).

Р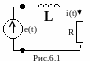 ешение. Комплексная амплитуда ЭДС E(jω) = Ee^jφo.

Комплексное сопротивление контура Z(jω) = R + jωL.

Комплексная амплитуда тока в контуре по закону Ома равна I(jω) = E(jω)/(R + jωL). В показательной форме это выражение принимает вид:

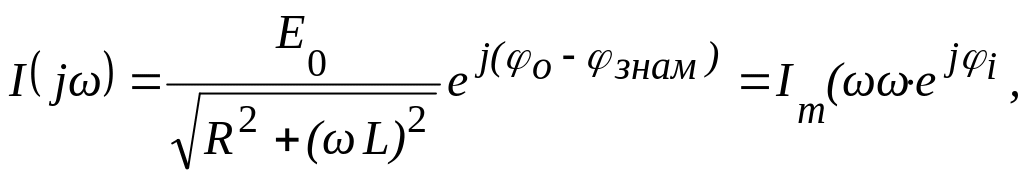
где ,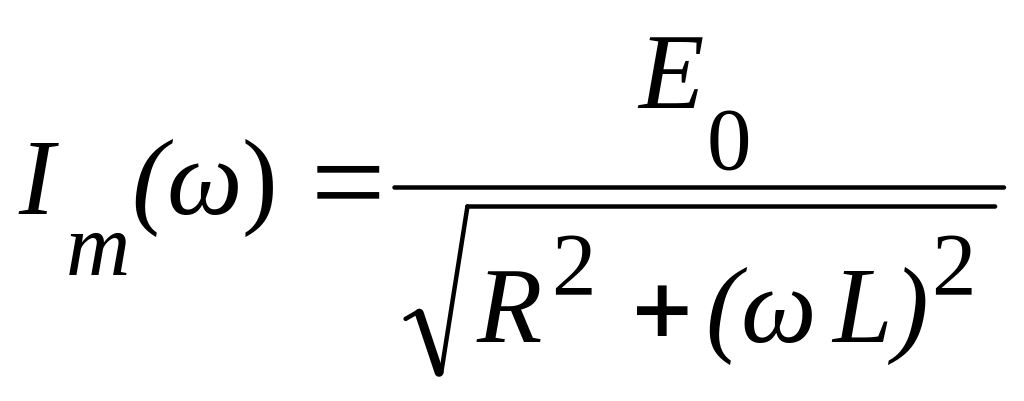

П ропуская промежуточную запись (6.2), запишем мгновенное значение тока по формуле 6.3

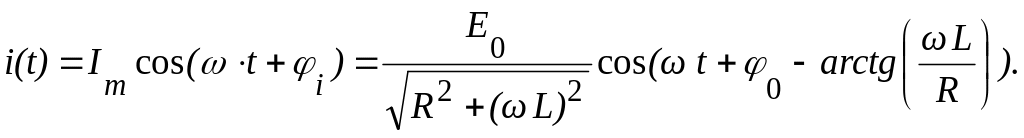(6.4)

6.2. Вывод формулы комплексной передаточной функции

В любой электрической цепи можно выделить пару зажимов (полюсов) – (1 – 1'), к которым подключается независимый источник (генератор), задающий внешнее воздействие. Эту пару называют входными полюсами (рис. 6.2).

В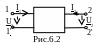 месте с этим можно выделить участок цепи (ветвь) между двумя узлами, в котором требуется определить ток или напряжение – отклик. Эти узлы т.е. полюсы (2 – 2') называют выходными. Таким образом, сложная цепь может рассматриваться в виде четырехполюсника (рис. 6.2).

Важнейшей характеристикой линейной электрической цепи является комплексная передаточная функция T(jω).

К омплексная передаточная функция (КПФ) определяется как отношение комплексной амплитуды отклика цепи к комплексной амплитуде воздействия.

В зависимости от вида воздействия и отклика различают следующие виды КПФ.

1. Комплексный коэффициент передачи по напряжению

K_U(jω) = U₂(jω)/U₁(jω) = K_U(ω)e^jφu(ω),

где U₂(jω), U₁(jω) – комплексные амплитуды напряжений на выходе и на входе цепи; K_U(ω) = U₂/U₁, φ_U(ω) = φ_U2(ω) – φ_U1(ω) – модуль и аргумент K_U(jω).

2. Комплексный коэффициент передачи по току

K_I(jω) = I₂(jω)/I₁(jω) = K_I(ω)e^jφi(ω),

Где i2(jω), i1(jω) – комплексные амплитуды токов на выходе и на входе цепи;

K_I(ω) = I₂/I₁, φ_i(ω) = φ_i2(ω) – φ_i1(ω) – модуль и аргумент K_I(jω).

3. Комплексное передаточное сопротивление

Z₂₁(jω) = U₂(jω)/I₁(jω) = Z₂₁(ω)e^jφz(ω).

4. Комплексная передаточная проводимость

Y₂₁(jω) = I₂(jω)/U₁(jω) = Y₂₁(ω)e^jφy(ω).

К омплексная передаточная функция как и всякое комплексное число может быть записана в показательной, тригонометрической и алгебраической форме соответственно:

T(jω) = T(ω)e^jφ(ω),

T(j) = T()cos φ(ω) + j T()sin φ(ω), (6.5)

T(j) = A() + j B().

T(ω) – модуль КПФ равен отношению амплитуд отклика и воздействия.

Зависимость модуля T(ω) от частоты ω называется амплитудно-частотной характеристикой (АЧХ) цепи.

φ(ω) – аргумент КПФ равен разности начальных фаз отклика и воздействия.

Зависимость аргумента φ(ω) от частоты ω называется фазо-частотной характеристикой (ФЧХ) цепи.

A() = T()cos φ(ω) и B() = T()sin φ(ω) – вещественная и мнимая части КПФ.

АЧХ и ФЧХ цепи, которые строятся раздельно, образуют комплексную частотную характеристику (КЧХ) цепи. АЧХ и ФЧХ можно изобразить и в виде одной зависимости, называемой амплитудно-фазовой характеристикой или годографом КПХ. В этом случае строят зависимость КПФ T(j) от частоты ω на комплексной плоскости. Годограф представляет собой геометрическое место концов вектора T(jω) = A(ω) + jB(ω) соответствующих изменению частоты от нуля до бесконечности. На годографе указываются точки, соответствующие некоторым значениям частоты, и стрелкой показывают направление перемещения конца вектора при увеличении частоты.

На рис. 6.3 показаны примеры характеристик комплексного коэффициента передачи: АЧХ –а), ФЧХ – б), АФХ – в).

К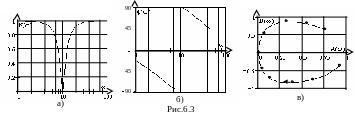 омплексная передаточная функция T(jω) рассчитывается методом комплексных амплитуд, по которому токи и напряжения представляются комплексными амплитудами İ = I(jω), Ŭ = U(jω), а сопротивления и проводимости - комплексными параметрами. Для удобства в промежуточных аналитических расчетах в комплексных функциях производят замену переменных. Например, K(jω) = K(p), jωL = pL, 1/jωC = 1/pC и т.д.

Переменная p = s + jω называется комплексной частотой.

В результате такой замены передаточная функция (6.5) представляется дробно–рациональной функцией T(p) переменной p. T(p) называют операторной передаточной функцией

(6.6)

Для упрощения дальнейших численных расчетов принято нормировать числитель на коэффициент a_m, а знаменатель – на коэффициент b_n. Тогда выражение (6.6) примет окончательный вид

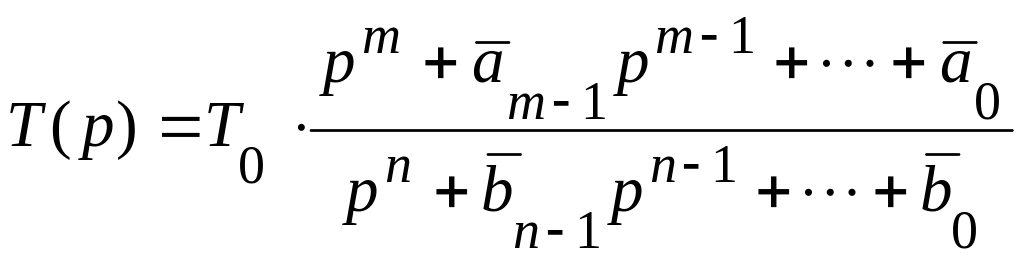, (6.7)

где

П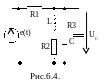 ример 6.2. Получить выражение операторного коэффициента передачи по напряжению на емкости K_UC(p) = U_C(p)/E(p) для схемы, изображенной на рис. 6.4. R1 = 10 кОм, R2 = 10 Ом,

R3 = 100 кОм, L = 1 мГн, C = 10 пФ.

Решение. Напряжение U_UC(p) является откликом в данной задаче, который нужно рассчитать. Для этого можно применить известные методы расчета цепей (метод узловых напряжений, контурных токов, метод четырехполюсника и др.). Наиболее просто эта задача решается методом узловых напряжений. Для этой схемы нужно записать только одно уравнение по первому закону Кирхгофа, так как в схеме один независимый узел.

Таким образом,

(6.8)

После подстановки значений параметров элементов в формулу (6.8) получится численное выражение коэффициента передачи

. (6.9)

Поделим числитель и знаменатель на коэффициенты a_m и b_n и представим выражение (6.9) в виде формулы (6.7)

. (6.10)