
- •Кафедра информационных технологий
- •Москва – 2007
- •Содержание
- •Введение
- •Постановка задачи
- •Решение задачи
- •Глава 2. Оптимизация технологий рецептурных смесей
- •2.1. Оптимизация технологии составления многокомпонентных рецептурных смесей
- •1. Формирование математической модели
- •2. Формирование компьютерной модели
- •3. Поиск решения
- •2.2. Моделирование двух- и трёхкомпонентной рецептурной смеси
- •1. Модель показателя активной кислотности (pH)
- •2. Модель водосвязывающей способности (всс)
- •Глава 3. Регрессионно-факторный анализ в исследовании адекватности эмпирических зависимостей
- •3.1. Идентификация параметров эмпирических зависимостей технологических моделей
- •3.2. Адекватность эмпирических зависимостей
- •Критерий поворотных точек для определения случайности остаточной компоненты
- •Определение автокорреляции остатков критерием Дарбина-Уотсона
- •Независимость распределения остаточной компоненты по r/s-критерию
- •3.3. Оценка статистической значимости регрессионных моделей технологических объектов
- •Коэффициент детерминации как характеристика силы вязи между показателями исследуемого технологического объекта
- •Оценка качества уравнения регрессии f-критерием Фишера
- •Оценка статистической значимости коэффициентов регрессии и корреляции t-критерием Стьюдента
- •Постановка задачи
- •Зависимость щёлочности и показателя активной кислотности рН от объёмной доли спирта
- •Решение задачи
- •Глава 4. Спектральные методы оценки нечетких потребительских свойств пищевого сырья и готовых продуктов
- •4.1. Сверхразрешение при различии спектральных распределений Постановка задачи
- •Решение задачи
- •4.2. Сравнительный анализ технологий. Моделирование связи показателей технологий
- •Список литературы
3.1. Идентификация параметров эмпирических зависимостей технологических моделей
Классический
подход к оцениванию параметров линейной
регрессии
![]() или
или
![]() основан
на методе наименьших квадратов (МНК).
основан
на методе наименьших квадратов (МНК).
МНК
позволяет получить такие оценки
параметров a
и b,
при которых сумма квадратов отклонений
фактических значений у
результативного признака от расчетных
(теоретических)
![]() (
(![]() )
минимальна:
)
минимальна:
![]() , (3.1)
, (3.1)
т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:
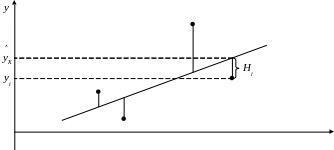
Для
нахождения минимума функции ОШ
требуется вычислить частные производные
функции
![]() по
параметрам а
и b
и приравнять их нулю:
по
параметрам а
и b
и приравнять их нулю:
![]() (3.2)
(3.2)
Итак,
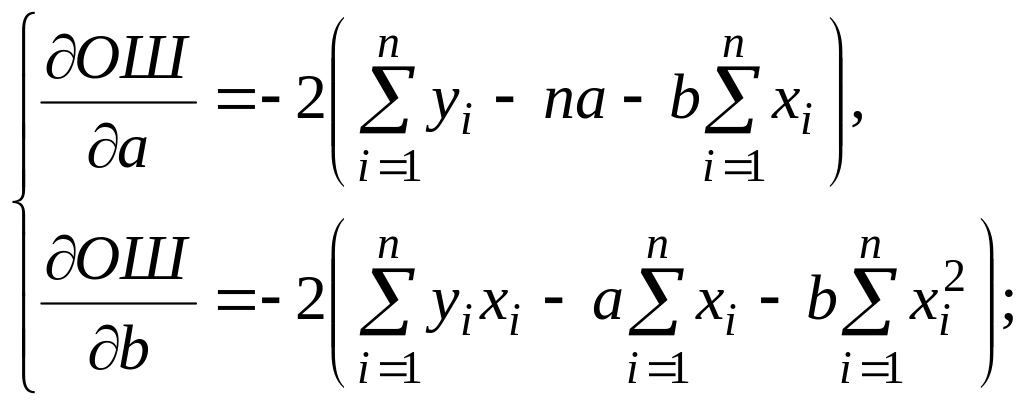 (3.3)
(3.3)
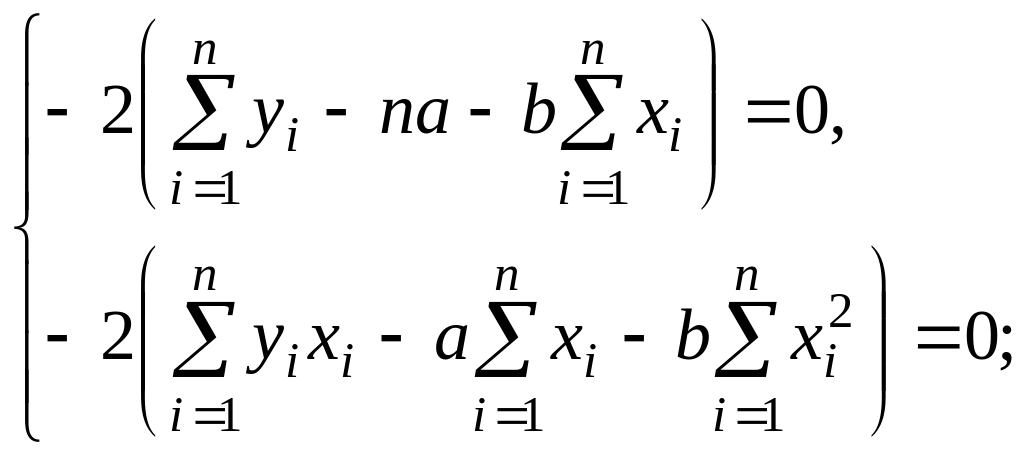 (3.4)
(3.4)
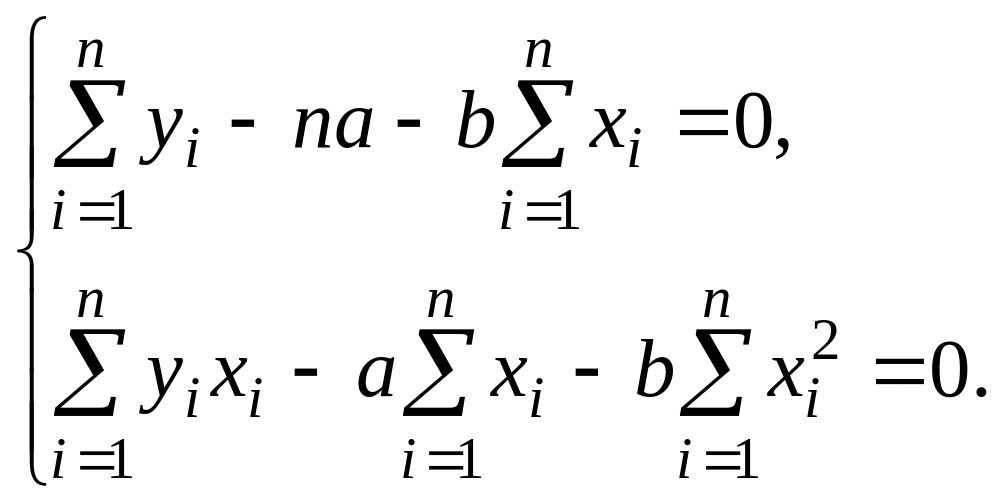 (3.5)
(3.5)
Таким образом, получаем, что
![]() (3.6)
(3.6)
где
![]() ‑ ковариация признаков;
‑ ковариация признаков;
![]() ‑ дисперсия
признака х.
‑ дисперсия
признака х.
Следовательно,
![]() (3.7)
(3.7)
Рассмотрим применение метода наименьших квадратов на примере идентификации параметров модели смеси с равноправными компонентами.
Пусть имеется трёхкомпонентная модель, в которой смесь представляет собой совокупность компонентов трёх типов. Тогда модель трёхкомпонентной смеси с учётом зависимости поправки от массовых долей компонентов можно представить в виде
![]() (3.8)
(3.8)
неизвестные параметры которого подлежат идентификации.
Составляется
несколько смесей с различными массовыми
долями
![]() ,
,
![]() ,
,
![]() (n
‑ номер
комбинации смеси) и при каждой n-й
комбинации
смеси измеряется значения
(n
‑ номер
комбинации смеси) и при каждой n-й
комбинации
смеси измеряется значения
![]() физической величины Y,
вычисляется значение
физической величины Y,
вычисляется значение
![]() при известных параметрах
при известных параметрах
![]() .
.
Для
идентификации неизвестных параметров
минимизируется суммарная ошибка
![]() (остаток, описывающий ошибку использованной
модели,
(остаток, описывающий ошибку использованной
модели,
![]() ,
т.к. зависит от номера замера n).
,
т.к. зависит от номера замера n).
Из уравнения (3.8) выражаем
![]() (3.9)
(3.9)
Далее используем условие минимизации функции
![]() (3.10)
(3.10)
Применяя,
например, линейное приближение зависимости
поправки от массовых долей (![]() ),
из данных условий получим следующую
систему 3-х линейных уравнений, определяющих
3 искомых коэффициента модели:
),
из данных условий получим следующую
систему 3-х линейных уравнений, определяющих
3 искомых коэффициента модели:
![]() (3.11)
(3.11)
Детерминант
D
данной системы уравнений (с учетом
зависимости
![]() ,
равен
,
равен
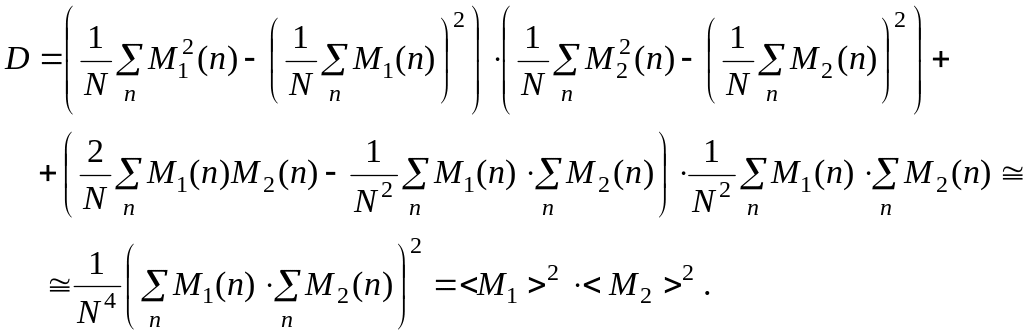 (3.12)
(3.12)
Таким образом, система уравнений всегда имеет решение.
3.2. Адекватность эмпирических зависимостей
Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии Нi.
Исследование остатков Нi предполагает проверку 5 предпосылок МНК:
‑ случайный характер остатков (критерий поворотных точек);
‑ нулевая средняя величина остатков, не зависящих от xi;
‑ гомоскедастичность – дисперсия каждого отклонения Нi одинакова для всех значений х;
‑ отсутствие автокорреляции остатков. Значения остатков Нi распределены независимо друг от друга (критерий Дарбина-Уотсона);
‑ остатки подчиняются нормальному распределению (независимость распределения остаточной компоненты по R/S-критерию).
Рассмотрим вышеперечисленные критерии.
Критерий поворотных точек для определения случайности остаточной компоненты
Определяется количество поворотных точек по величинам остатков Нi. При этом точка будет считаться поворотной, если она одновременно больше или меньше соседних с ней точек.
Случайность остаточной компоненты по критерию поворотных точек подтверждается, если выполняется неравенство
![]() , (3.13)
, (3.13)
где М – число поворотных точек, n – число измерений в выборке.
