
- •Высшего профессионального образования
- •Г. Набережные Челны
- •1.Цель и задачи дисциплины, её место в учебном процессе.
- •2. Содержание и структура дисциплины.
- •Тема 5. Линии на плоскости.
- •Раздел II. Введение в анализ. Дифференциальное исчисление.
- •Тема 6. Множества. Числовые множества. Функции.
- •Тема 7. Числовые последовательности и ряды. Предел последовательности. Предел функции и непрерывность.
- •Тема 8. Производная и дифференциал функции.
- •Тема 9. Исследование функций с помощью производных, построение их графиков.
- •3. Рекомендуемая литература. Основная литература:
- •Дополнительная литература:
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •5.1. Задания для контрольной работы.
- •Раздел I. Аналитическая геометрия и линейная алгебра.
- •Раздел II. Введение в анализ. Дифференциальное исчисление.
- •Раздел III. Интегральное исчисление.
- •Раздел IV. Дифференциальные уравнения.
- •Раздел V. Теория вероятностей и математическая статистика.
- •5.2. Вопросы к экзамену.
- •Раздел I. «Аналитическая геометрия и линейная алгебра».
- •Раздел II. Введение в анализ. Дифференциальное исчисление.
- •Раздел III. Интегральное исчисление.
- •Раздел IV. Дифференциальные уравнения.
- •Раздел V. Теория вероятностей и математическая статистика.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта.
- •Раздел I. Аналитическая геометрия и линейная алгебра.
- •Раздел II. Введение в анализ. Дифференциальное исчисление.
- •Раздел III. Интегральное исчисление.
- •Раздел IV. Дифференциальные уравнения.
- •Раздел V. Теория вероятностей и математическая статистика.
- •Для решения задач с использованием формул сложения и умножения вероятностей следует:
- •6.2. Краткие теоретические сведения.
- •Тема 1. Определители.
- •Тема 2. Матрицы.
- •Тема 3. Системы линейных алгебраических уравнений.
- •Тема 4. Векторы.
- •Тема 5. Линии на плоскости.
- •Тема 10. Множества. Числовые множества. Функции.
- •Тема 7. Числовые последовательности и ряды. Предел последовательности. Предел функции и непрерывность.
- •Тема 8. Производная и дифференциал функции.
- •Тема 9. Исследование функций с помощью производных, построение их графиков.
- •Тема 10. Неопределённый интеграл.
- •Тема 11. Определённый интеграл. Несобственные интегралы.
- •Основные свойства определённого интеграла:
- •Тема 12. Дифференциальные уравнения первого порядка.
- •Тема 13. Дифференциальные уравнения высших порядков.
- •Тема 14. Случайные события и их вероятности.
- •Тема 15. Случайные величины.
- •Тема 16. Элементы математической статистики. Предварительная обработка статистических данных.
- •6.3 Основные математические формулы.
- •6.4 Образец оформления обложки с контрольной работой. Федеральное агентство по образованию Государственное образовательное учреждение
- •«Камская государственная инженерно-экономическая академия»
- •Набережные Челны
6. Приложения.
6.1. Образец решения контрольных задач типового варианта.
Раздел I. Аналитическая геометрия и линейная алгебра.
1-10.
Найти матрицу
![]() ,
если:
,
если:
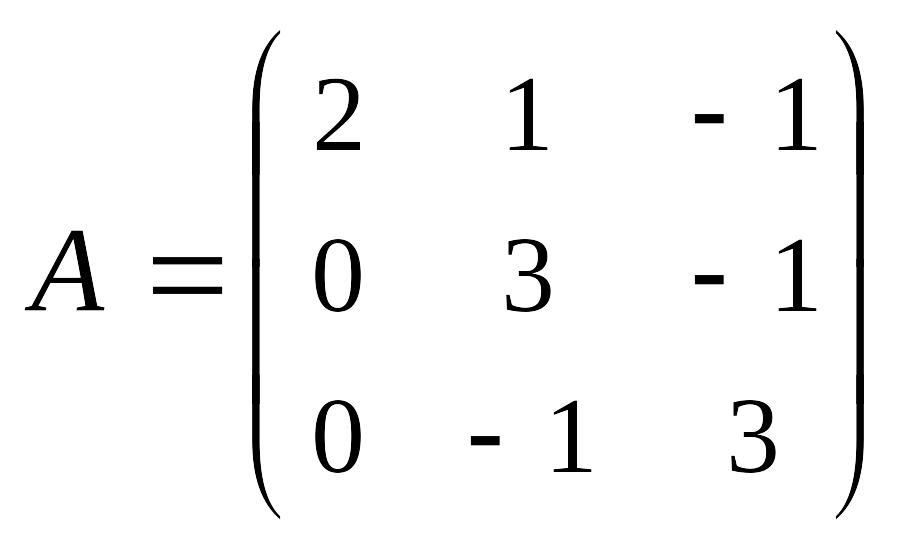 ,
,
 .
.
Решение:
1)
Транспонируем
матрицу
![]() :
:
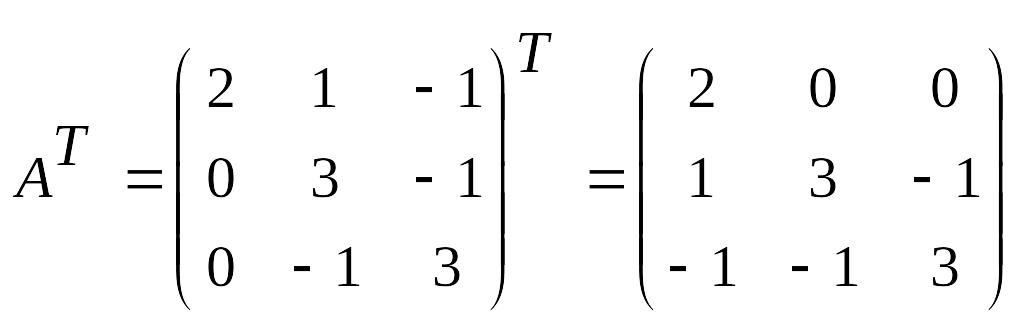 .
.
2)
Вычисляем
произведение матриц
![]() :
:
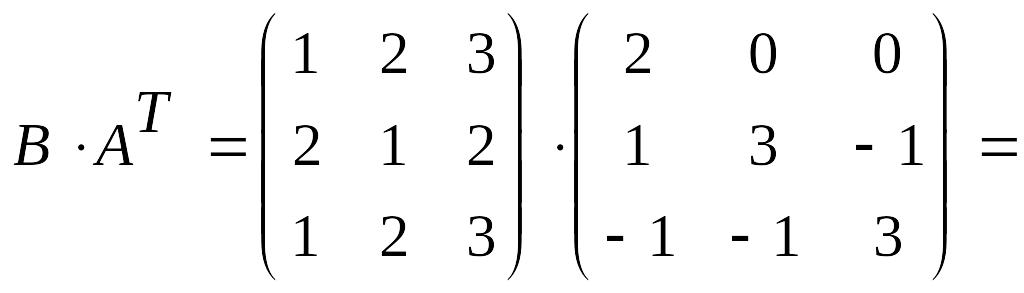

 .
.
3)
Находим
матрицу
![]() :
:
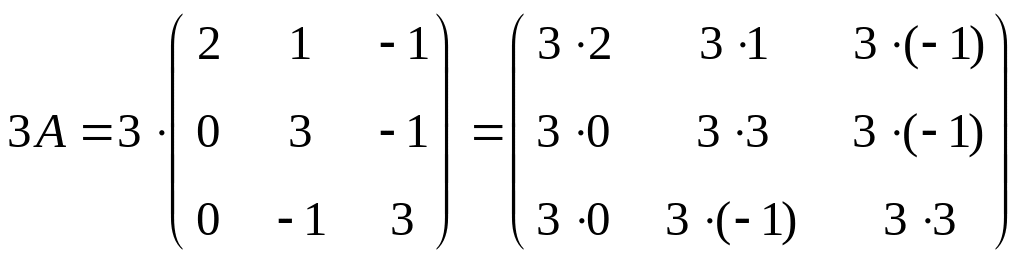
 .
.
4)
Находим
матрицу
![]() :
:
![]()
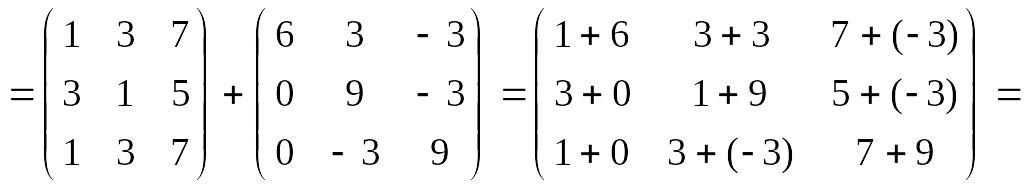
 .
.
Ответ:
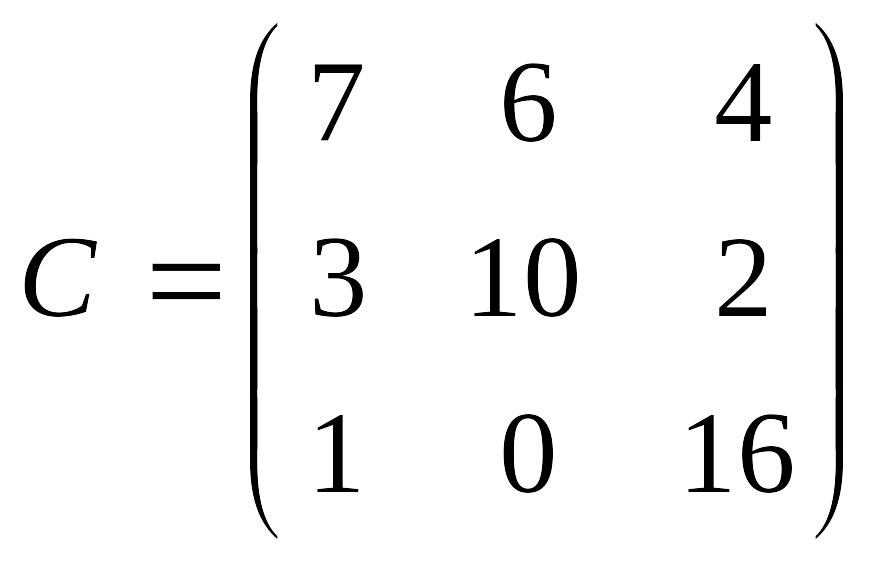 .
.
11 – 20. Дана
система уравнений:
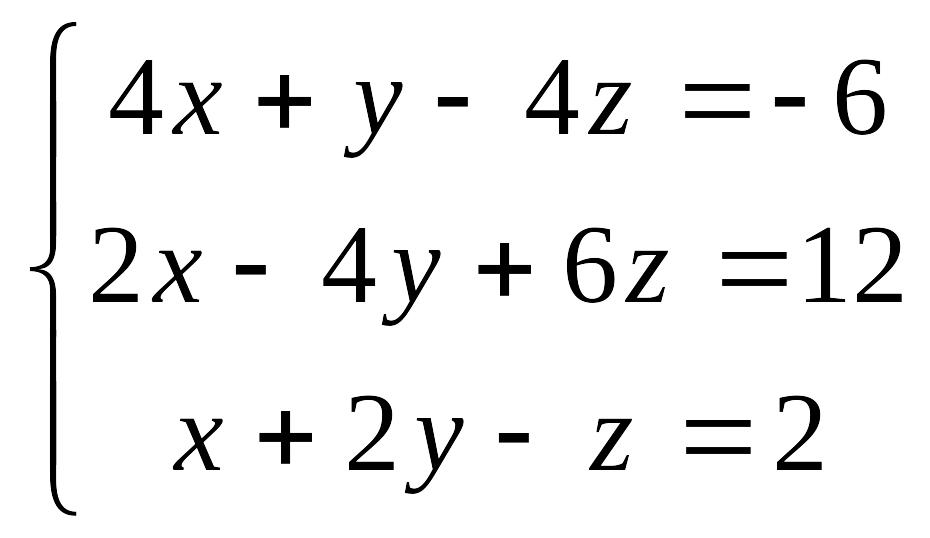 .
Требуется:
.
Требуется:
а) найти решение системы методом Крамера;
б) найти решение системы методом Гаусса.
Решение.
А) Метод Крамера.
1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:
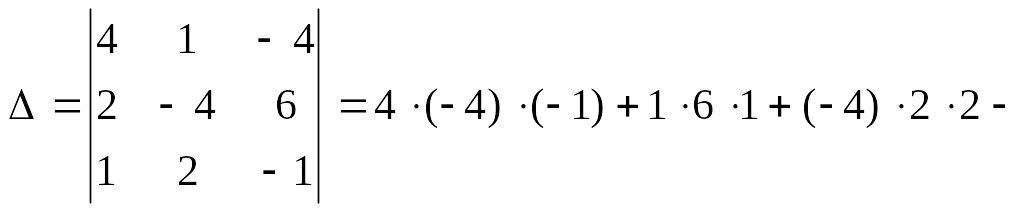
![]() .
.
2а)
Так как
![]() ,
то система имеет единственное решение,
определяемое формулами Крамера:
,
то система имеет единственное решение,
определяемое формулами Крамера:
![]()
3а)
Вычисляем
определители
![]() :
:

![]() ,
,
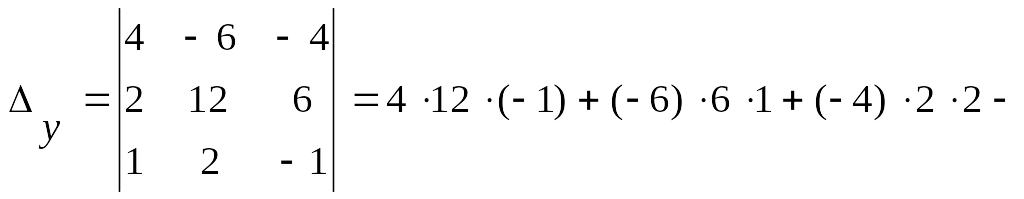
![]() ,
,
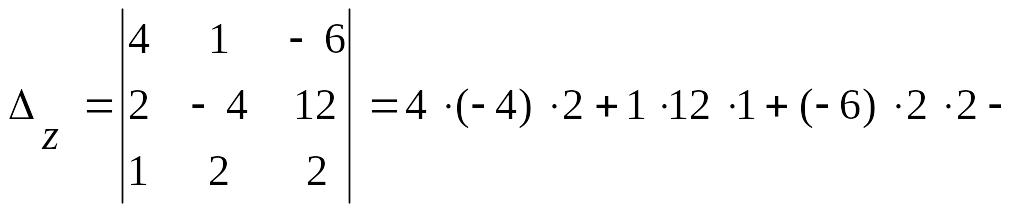
![]() .
.
4а)
Находим решение:
![]() .
.
5а)
Выполняем
проверку:
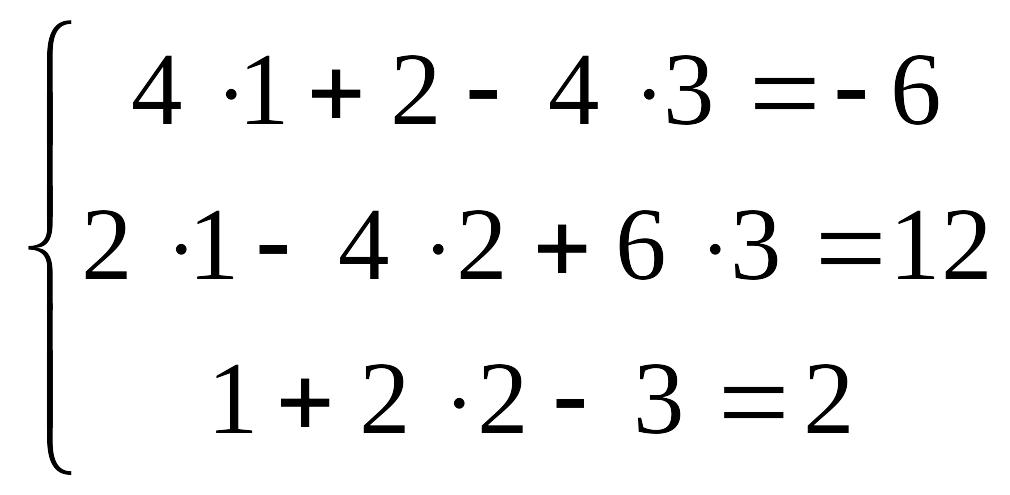
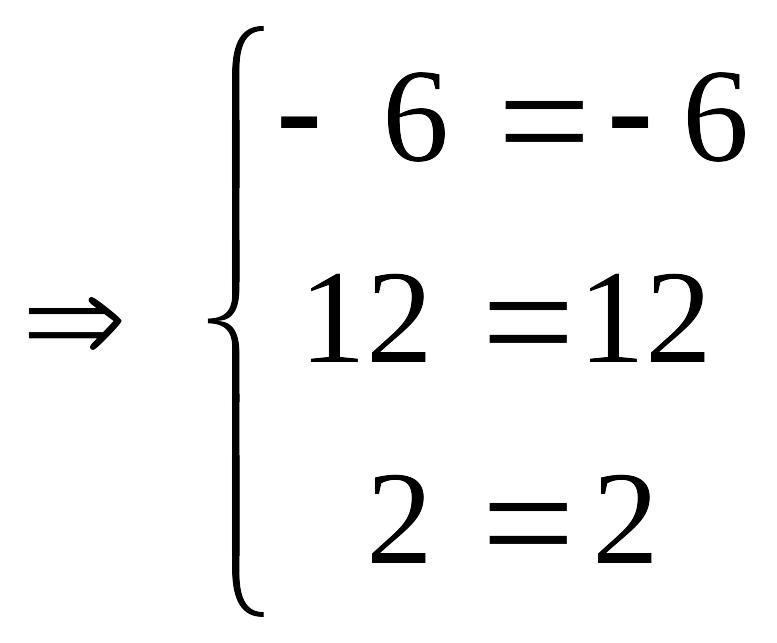 .
.
Ответ:
![]() .
.
Б) Метод Гаусса.
1б) Записываем расширенную матрицу системы:
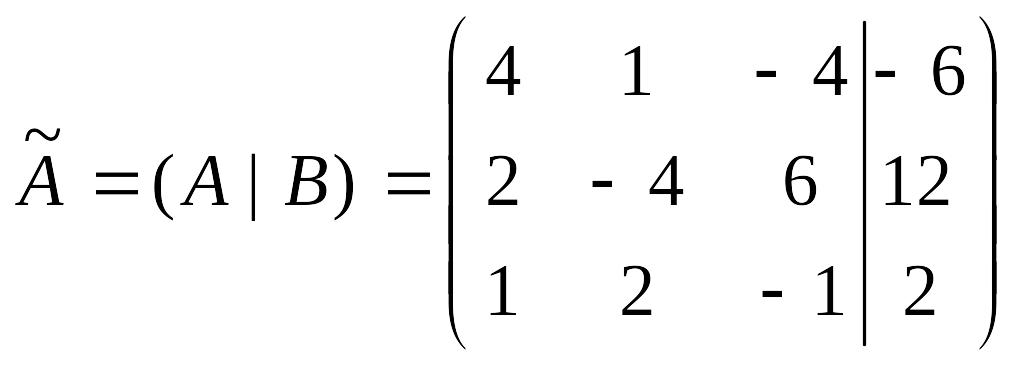 .
.
2б) Выполняем прямой ход метода Гаусса.
В
результате прямого хода матрица системы
![]() должна быть преобразована с помощью
элементарных преобразований строк к
матрице
должна быть преобразована с помощью
элементарных преобразований строк к
матрице
![]() треугольного или трапециевидного вида
с элементами
треугольного или трапециевидного вида
с элементами
![]() .
Система уравнений, матрица которой
является треугольной с элементами
.
Система уравнений, матрица которой
является треугольной с элементами
![]() ,
имеет единственное решение, а система
уравнений, матрица которой
является трапециевидной с элементами
,
имеет единственное решение, а система
уравнений, матрица которой
является трапециевидной с элементами
![]() ,
имеет бесконечно много решений.
,
имеет бесконечно много решений.
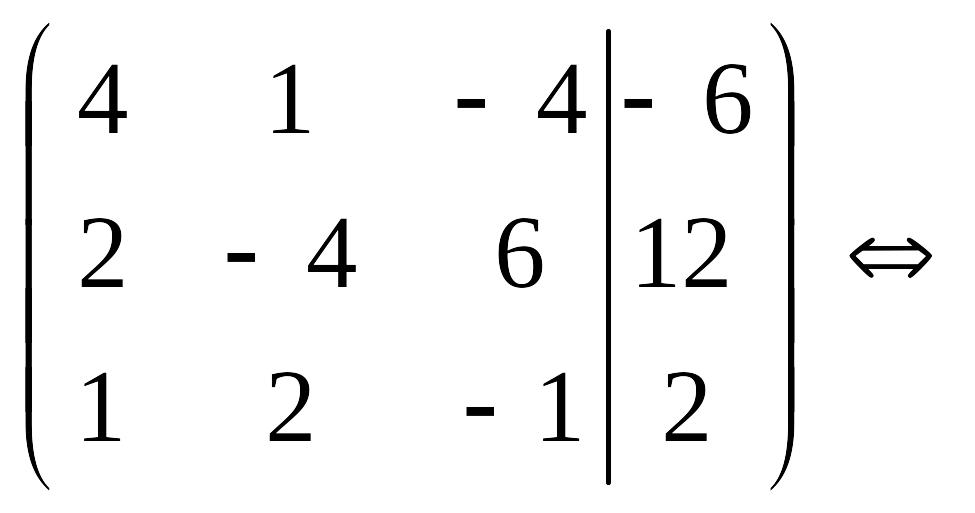
![]()
![]()

![]()
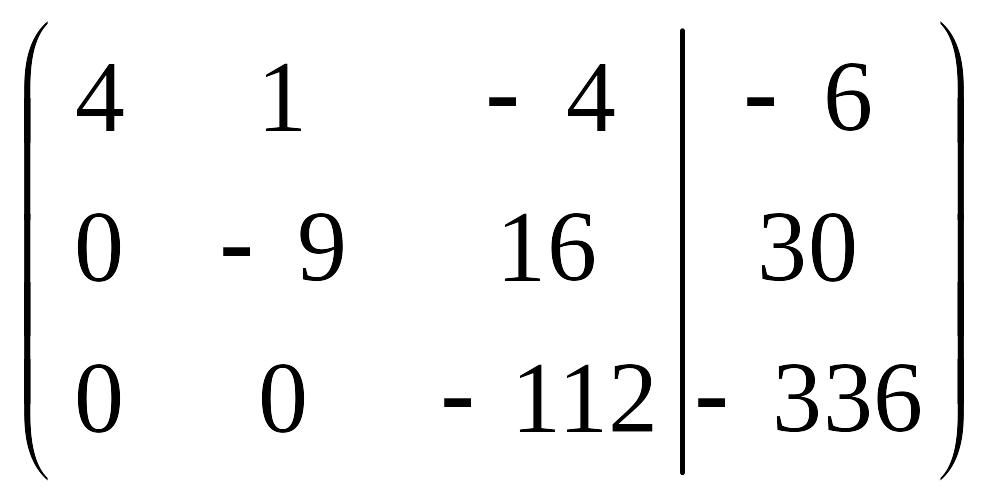 .
В результате
элементарных преобразований матрица
системы преобразована к специальному
виду
.
В результате
элементарных преобразований матрица
системы преобразована к специальному
виду
![]() .
Система уравнений, матрица которой
,
является треугольной с ненулевыми
диагональными элементами
,
имеет всегда единственное решение,
которое находим, выполняя обратный ход.
.
Система уравнений, матрица которой
,
является треугольной с ненулевыми
диагональными элементами
,
имеет всегда единственное решение,
которое находим, выполняя обратный ход.
Если
при выполнение преобразования расширенной
матрицы
![]() в преобразованной матрице
в преобразованной матрице
![]() появляется строка
появляется строка
![]() ,
где
,
где
![]() ,
то это говорит о несовместности исходной
системы уравнений.
,
то это говорит о несовместности исходной
системы уравнений.
3б) Выполняем обратный ход метода Гаусса.
Записываем
систему уравнений, соответствующую
последней расширенной матрице прямого
хода:
 и последовательно из уравнений системы,
начиная с последнего, находим значения
всех неизвестных:
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех неизвестных: .
.
4б) Выполняем проверку: .
Ответ: .
21
– 30. Даны
векторы
![]() :
:
![]() ,
,
![]() ,
,
![]() .
Требуется: а)
найти векторы
.
Требуется: а)
найти векторы
![]() и
и
![]() ;
б) вычислить
скалярное произведение
;
б) вычислить
скалярное произведение
![]() ;
в) найти
проекцию вектора
на направление вектора
;
г)
найти векторное произведение
и его модуль
.
;
в) найти
проекцию вектора
на направление вектора
;
г)
найти векторное произведение
и его модуль
.
Решение.
a) Находим векторы и :
![]()
=![]()
![]() ;
;
![]()
=![]()
![]() .
.
б) Вычисляем скалярное произведение векторов :
![]() .
.
в) Находим проекцию вектора на направление вектора :
![]() .
.
г) Находим векторное произведение векторов :
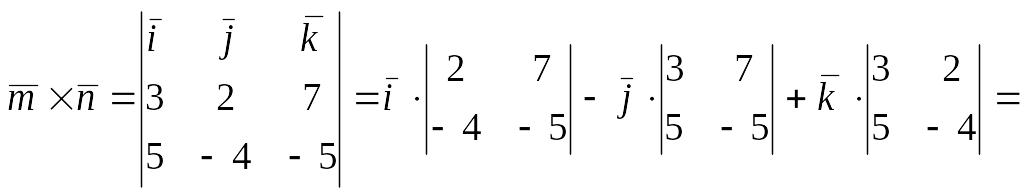
![]()
![]()
и
вычисляем его модуль:
=![]() .
.
Ответ:
а)
=
;
=
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ,
,
![]() .
.
31-40.
Даны вершины
треугольника
:
![]() ,
,
![]() ,
,
![]() Требуется сделать чертёж и найти:
Требуется сделать чертёж и найти:
а)
длину стороны
![]() ;
б) уравнение
стороны
;
;
б) уравнение
стороны
;
в)
длину
высоты
![]() ;
г) площадь
треугольника
;
г) площадь
треугольника
![]() ..
..
Решение. Сделаем чертёж:
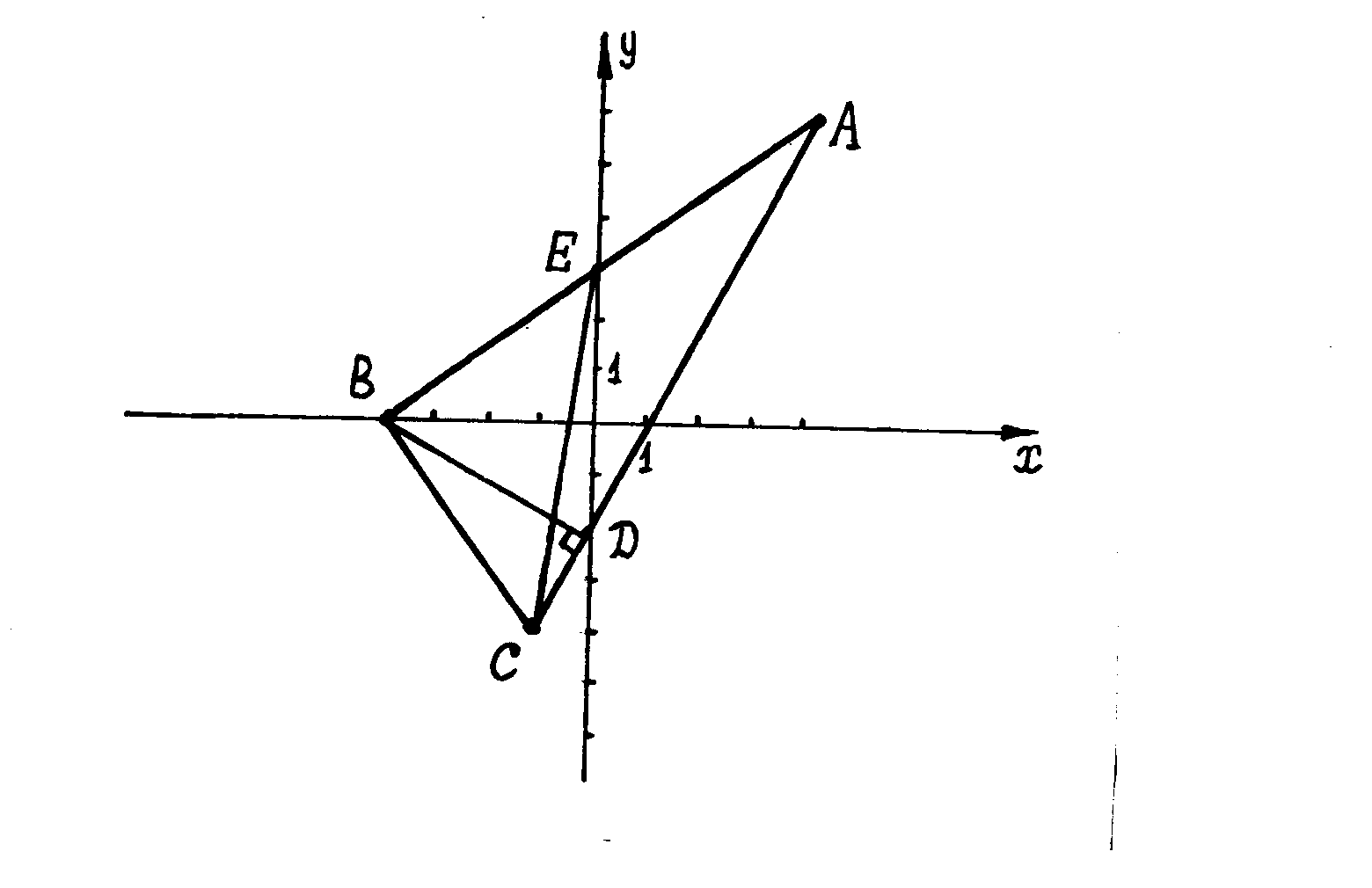
а)
Длину
стороны
находим как
длину вектора
![]() :
:
![]() ,
,
![]() .
.
б)
Уравнение
стороны
![]() находим как уравнение прямой, проходящей
через точки
находим как уравнение прямой, проходящей
через точки
![]() и
и
![]() ,
и записываем его в виде общего уравнения
прямой:
,
и записываем его в виде общего уравнения
прямой:
![]()
![]()
![]()
![]()
![]()
![]() .
.
в)
Длину
![]() высоты
находим как расстояние от точки
высоты
находим как расстояние от точки
![]() до прямой
,
заданной общим уравнением
до прямой
,
заданной общим уравнением
![]() :
:
![]() .
.
г)
Площадь
треугольника
находим по
формуле:
![]() .
Откуда
.
Откуда
![]() .
.
Примечание.
Площадь
треугольника
![]() можно найти и, используя геометрический
смысл векторного произведения векторов,
по формуле:
можно найти и, используя геометрический
смысл векторного произведения векторов,
по формуле:
![]() .
Учитывая, что
.
Учитывая, что
 ,
получим
,
получим
![]() .
.
Ответ:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
