Раздел IV. Дифференциальные уравнения.

131-140. Установить тип ДУ первого порядка и найти:

а) общее решение ДУ:

1а) 2а)

б) общее и частное решения ДУ: , .

Решение.

Тип ДУ первого порядка устанавливают по форме его записи.

1а) Данное уравнение является дифференциальным уравнением с разделяющимися переменными, так как его можно записать в виде

.

Действительно, осуществив в исходном уравнении замену и умножив его затем на , получим: , т.е. уравнение с разделяющимися переменными.

Нахождение общего решения уравнения , путём деления обеих его частей на , сводится к интегрированию уравнения с разделёнными переменными , где , , общее решение которого записывается в виде .

Разделим обе части уравнения на множитель , получим ДУ с разделёнными переменными: .

Общее решение последнего уравнения найдём интегрированием каждого слагаемого по своей переменной и запишем в виде:

, где - произвольная постоянная.

Общее решение дифференциального уравнения первого порядка должно обязательно содержать одну произвольную постоянную.

Вычислим интегралы (с точностью до постоянного слагаемого):

,

Тогда общее решение дифференциального уравнения запишется в виде:

.

Ответ: , где - произвольная постоянная.

2а) Данное уравнение является однородным дифференциальным уравнением первого порядка, так как его можно записать в виде . Действительно, выполнив преобразования: , получим .

При выполнении преобразований однородного ДУ первого порядка к виду следует учесть, что .

Нахождение общего решения однородного ДУ первого порядка с помощью подстановки , или , где - новая неизвестная функция, сводится к нахождению общего решения ДУ с разделяющимися переменными относительно функции с последующей заменой .

С помощью подстановки , уравнение или приведём к ДУ с разделяющимися переменными относительно новой неизвестной функции . Получим:

.

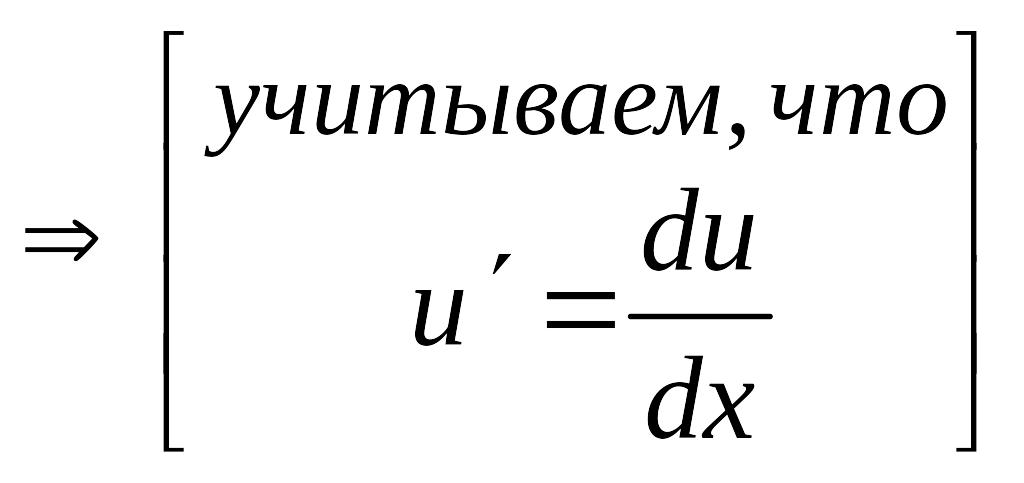
Последнее уравнение есть уравнение с разделяющимися переменными. Сведём его, разделив обе части уравнения на множитель к уравнению с разделёнными переменными. Получим: .

Общее решение последнего уравнения найдём интегрированием каждого слагаемого по своей переменной и запишем в виде:

, где - произвольная постоянная.

Вычислим интегралы (с точностью до постоянного слагаемого):

;

.

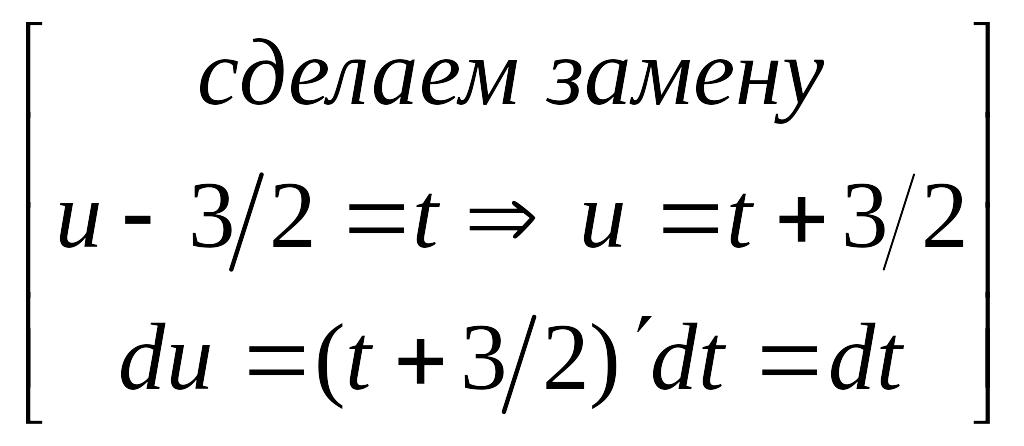
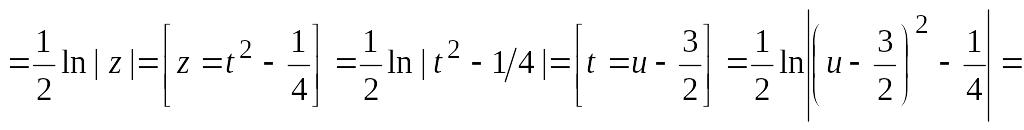
Тогда общее решение последнего дифференциального уравнения запишется в виде: или, используя свойства логарифмов, в виде: , где - новая произвольная постоянная.

Теперь в найденном решении вернёмся к старой неизвестной функции , выполнив обратную замену . В итоге получим:

или .

Ответ: , где - произвольная постоянная.

б) Данное уравнение является линейным дифференциальным уравнением (ЛДУ) первого порядка, так как его можно записать в виде , где , .

Сначала найдем общее решение линейного ДУ первого порядка. Его ищем в виде , где и - новые неизвестные функции.

Общее решение ЛДУ 1-го порядка находится с помощью подстановки , где , - новые неизвестные функции. Одну из них, например , находят в виде , где - какая-нибудь первообразная для функции , тогда другую неизвестную функцию находят в виде общего решения ДУ: . В итоге будет найдено и общее решение исходного уравнения в виде

Частное решение ДУ, удовлетворяющее начальному условию получают из общего решения данного уравнения при конкретном значении произвольной постоянной . Находят как решение уравнения, получаемого подстановкой в общее решение начального условия.

Функцию найдём в виде , где - какая-нибудь первообразная для функции . Вычислив интеграл, получим . Тогда .

Простейшим ДУ первого порядка называется уравнение вида . Общее решение такого уравнения находится интегрированием и записывается в виде .

Функцию найдём как общее решение ДУ: , где , . Данное уравнение является простейшим ДУ первого порядка. Его общее решение найдём интегрированием и запишем в виде . Вычислив интеграл (с точностью до постоянной), получим:

.

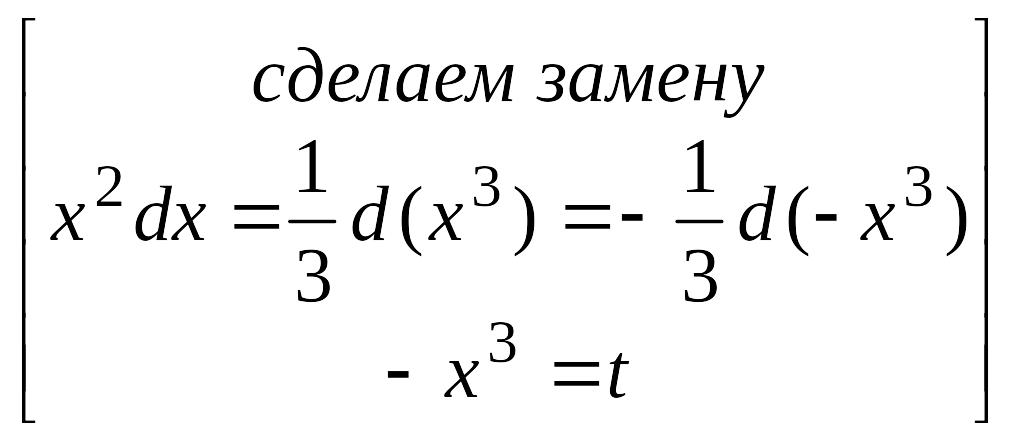
Таким образом .

Тогда общее решение исходного уравнения запишется в виде:

.

Теперь найдём частное решение, удовлетворяющее начальному условию . Его получим из общего решения при конкретном значении произвольной постоянной , которое найдём из уравнения, полученного подстановкой начального условия в общее решение. В результате получим: . Тогда частное решение исходного дифференциального уравнения, удовлетворяющее начальному условию , запишется в виде: .

Ответ: - общее решение; частное решение.

141-150. Требуется найти:

а) общее решение простейшего ДУ 2-ого порядка ;

б) общее и частное решения однородного линейного ДУ 2-ого порядка с постоянными коэффициентами: , , ;

в) общее решение линейного ДУ 2-ого порядка с постоянными коэффициентами и правой частью специального вида: .

Решение а).

Общее решение простейшего ДУ второго порядка находят, выполняя последовательно два интегрирования, и записывают в виде:

.

Общее решение дифференциального уравнения второго порядка должно обязательно содержать две разные произвольные постоянные.

Данное уравнение дважды проинтегрируем. После первого интегрирования получим: . Интеграл вычислим (с точностью до постоянного слагаемого) методом интегрирования по частям. Получим:

. Тогда .

После второго интегрирования получим: .

Вычислим интегралы (с точностью до постоянного слагаемого). Получим:

;

; .

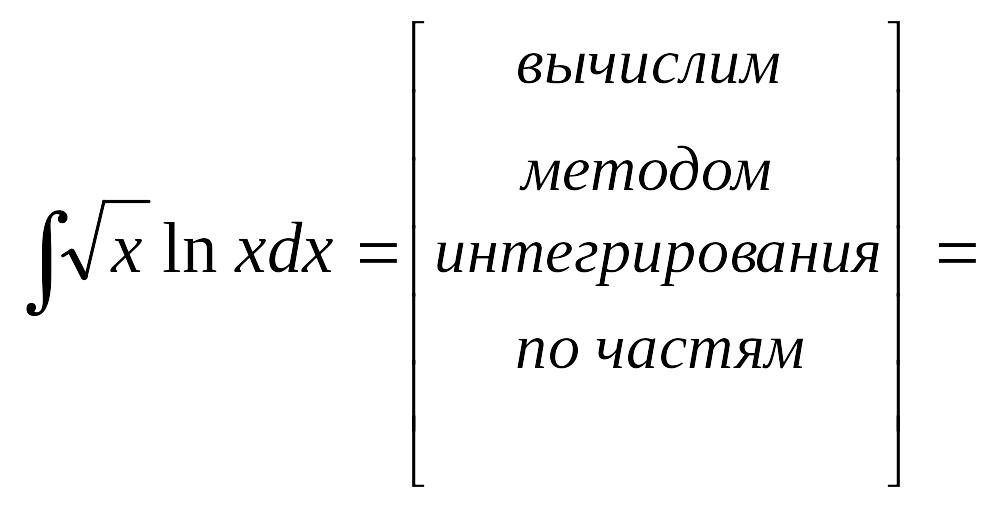
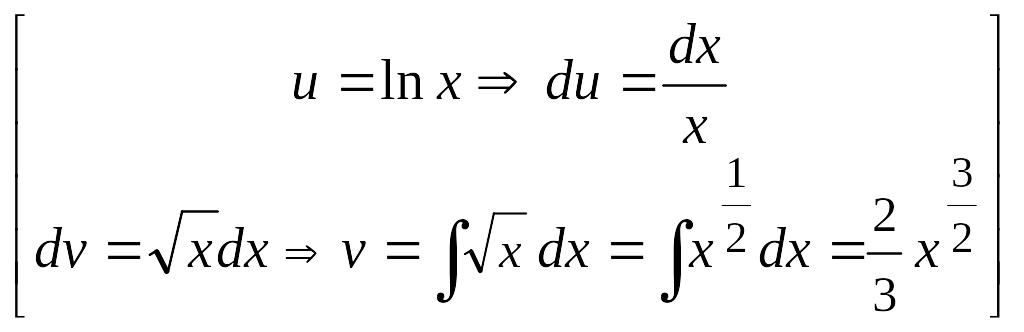
Тогда

.

Ответ: .

Решение б). Сначала найдём общее решение ДУ в виде: , где - фундаментальная система его частных решений.

Общее решение однородного линейного ДУ второго порядка с постоянными коэффициентами имеет вид , где - фундаментальная система его частных решений; -произвольные постоянные.

Фундаментальная система решений строится на основе характера корней характеристического уравнения . А именно:

1) если - пара различных действительных корней характеристического уравнения, то ФСР имеет вид ;

2) если - пара одинаковых действительных корней, то ФСР имеет вид ;

3) если - пара комплексно-сопряжённых корней, то ФСР имеет вид .

Корни характеристического уравнения , являющегося квадратным, находят на множестве комплексных чисел по формулам:

1) если дискриминант уравнения , то ;

2) если дискриминант уравнения , то .

Для нахождения ФСР, составим характеристическое уравнение для данного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант , то , , т.е. характеристическое уравнение имеет два различных действительных корня. Следовательно, ФСР имеет вид .

Тогда общее решение данного ДУ запишется в виде: .

Теперь найдём частное решение данного ДУ, удовлетворяющее начальным условиям: , . Для этого сначала найдём производную общего решения: . Затем подставим начальные данные в выражения для общего решения и его производной, получим систему линейных алгебраических уравнений для определения значений произвольных постоянных и :

.

Решив систему, найдём: , . Тогда частное решение данного ДУ запишется в виде: .

Ответ: ; .

Решение в).

Общее решение неоднородного ЛДУ 2-го порядка имеет вид , где - общее решение соответствующего однородного уравнения, - какое-нибудь частное решение данного неоднородного уравнения.

Частное решение уравнения с правой частью специального вида ищется методом неопределённых коэффициентов в виде , где , если число не является корнем характеристического уравнения, и равно кратности корня в противном случае; и - полные многочлены степени с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени соответственно являются: , , , ,…. Для нахождения коэффициентов многочленов и , надо подставить решение в неоднородное дифференциальное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.

Общее решение данного ДУ найдём в виде: , где - фундаментальная система частных решений соответствующего ему однородного ДУ: ; - какое-нибудь частное решение данного неоднородного дифференциального уравнения.

Сначала найдём ФСР соответствующего однородного ДУ . Для этого составим характеристическое уравнение для данного однородного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант , то , , т.е. характеристическое уравнение имеет два одинаковых действительных корня. Следовательно, ФСР имеет вид .

Затем найдём частное решение неоднородного уравнения , имеющего правую часть специального вида , где , , , . Частное решение найдём в виде , где , если число не является корнем характеристического уравнения, и равно кратности корня в противном случае; и - полные многочлены степени с неопределёнными коэффициентами. В данном случае: число не является корнем характеристического уравнения, поэтому ; , поэтому , , где - неизвестные постоянные, подлежащие определению. Таким образом, частное решение с неизвестными постоянными запишется в виде:

.

Для определения значений постоянных и , найдём производные

и подставим выражения для вместо в неоднородное уравнение . Учитывая, что:

, ,

получим:

.

Приравняв, в правой и левой части полученного равенства, постоянные коэффициенты, стоящие при одинаковых функциях, получим систему линейных алгебраических уравнений относительно неизвестных и : . Решив систему, найдём: , . Частное решение запишется тогда в виде: .

Теперь запишем общее решение исходного уравнения в виде:

.

Ответ: .