Раздел III. Интегральное исчисление.

101-110. Найти неопределённые интегралы: a) непосредственным интегрированием; б) заменой переменной интегрирования; в) интегрированием по частям.

а) ;

б1) ; б2) ; б3) ;

в) ;

Нахождение неопределённого интеграла состоит в таком преобразовании подынтегрального выражения , чтобы получить интегралы (возможно по новой переменной интегрирования) из таблицы основных интегралов (приложение 6.3).

Решение.

а) Интеграл вычислим непосредственным интегрированием. Получим:

.

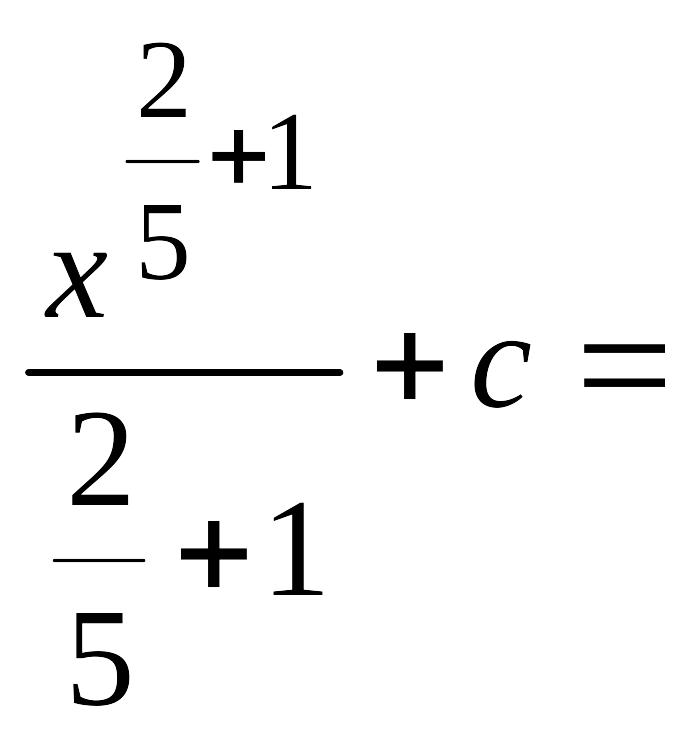
б1) Интеграл вычислим методом замены переменной интегрирования.

Интеграл вида , где - многочлен порядка , находят методом замены переменной с помощью подстановки .

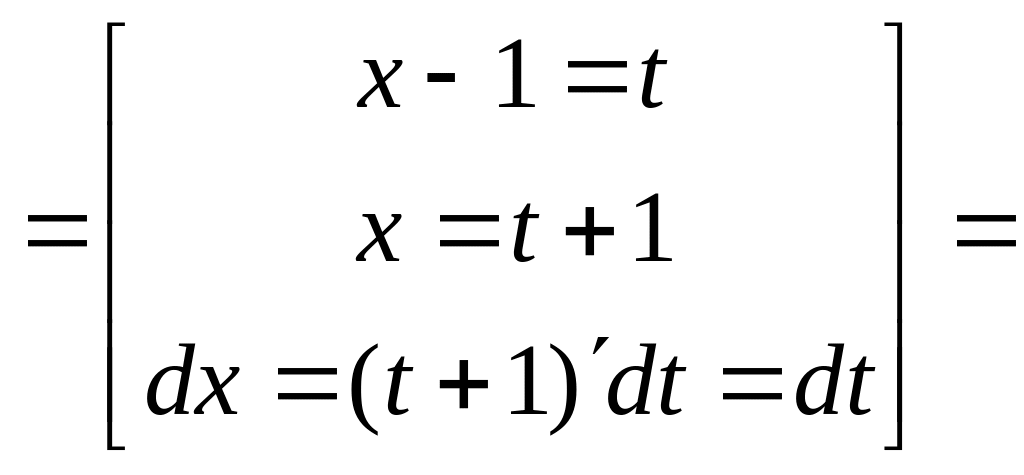
б2) Интеграл относится к интегралам вида . Для его вычисления сначала выделим полный квадрат в знаменателе подынтегральной функции, затем сделаем замену переменной интегрирования. Получим:

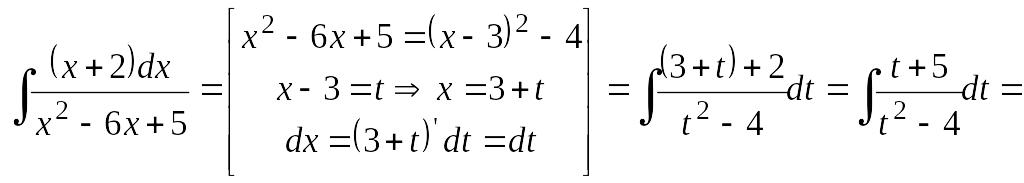
=[представляем интеграл в виде суммы интегралов] .

Вычислим каждый из интегралов в отдельности:

1)

.

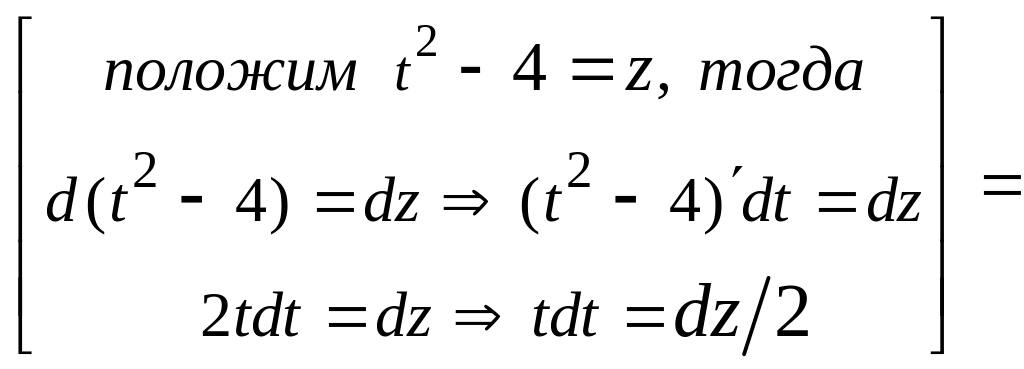
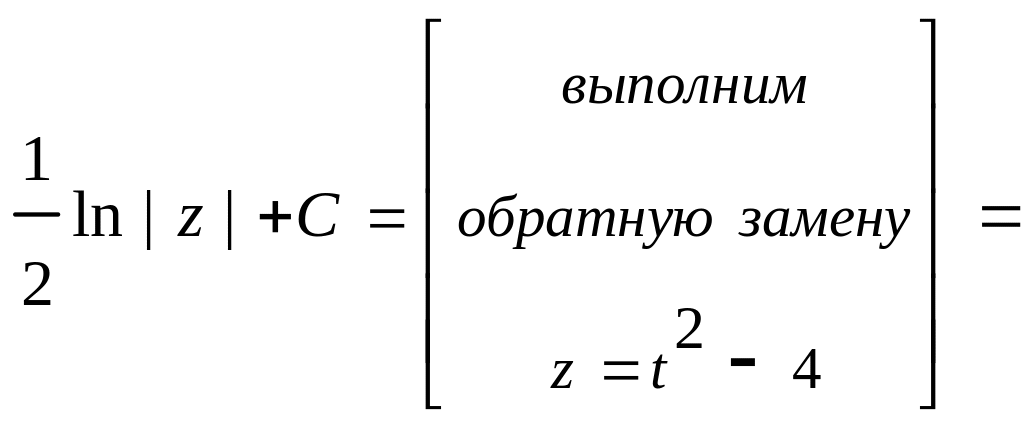
2)

Тогда:

.

Конечное выражение для неопределённого интеграла записывают, указывая одну из первообразных и добавляя к ней произвольную постоянную .

б3) Интеграл вычислим методом замены переменной интегрирования. Получим:

.

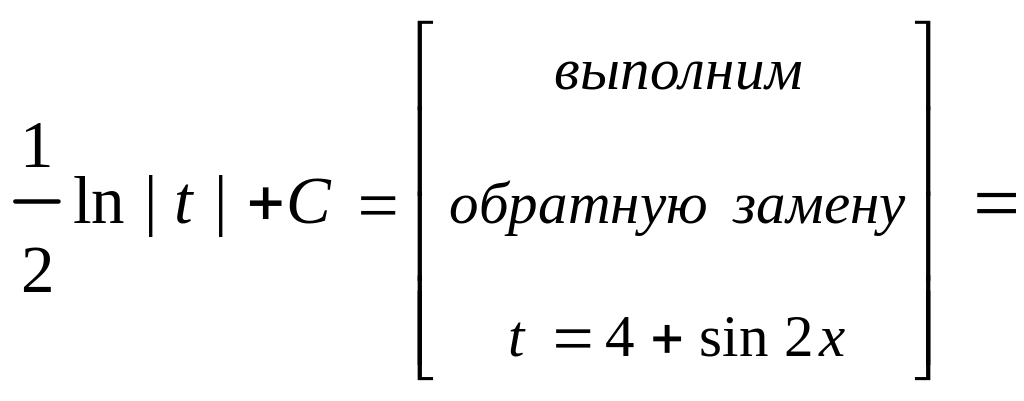
в) Интеграл вычислим методом интегрирования по частям, используя формулу .

Положим: , . Найдём ,

.

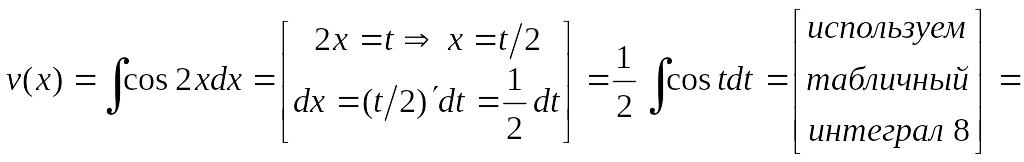
Интеграл в формуле интегрирования по частям вычисляется с точностью до постоянной, т.е. в качестве функции выбирается одна из первообразных для функции .

Для вычисления интеграла можно использовать и следующее свойство неопределённого интеграла: если , то , где - табличный интеграл. В данном случае, так как , то .

Тогда, получим:

Определённый интеграл для функции , непрерывной на отрезке , вычисляют по формуле Ньютона-Лейбница: , где -одна из её первообразных, используя для нахождения все приёмы и методы вычисления неопределённых интегралов.

Следствиями формулы Ньютона-Лейбница являются:

1) формула интегрирования по частям , где функции и непрерывно дифференцируемы на ;

2) формула замены переменной интегрирования

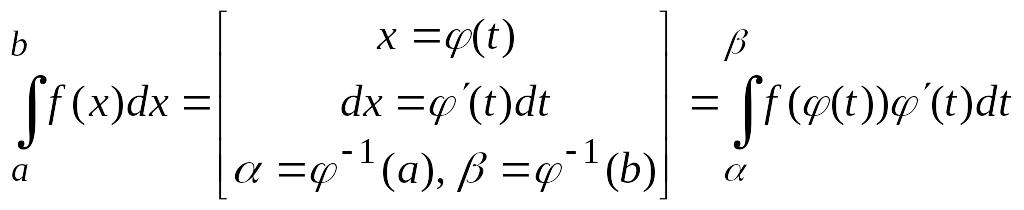, где функция - непрерывно дифференцируема на отрезке .

Часто замена переменной в определённом интеграле выполняется с помощью подстановки по формуле: 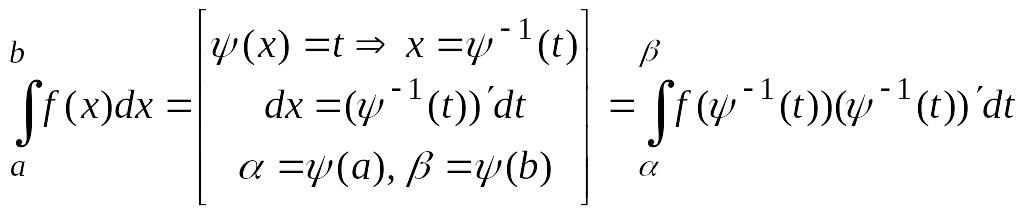, где функция - непрерывно дифференцируема на отрезке .

111-120. Требуется вычислить: а) определённый интеграл ;

б) несобственный интеграл (или установить его расходимость).

Решение.

а) Определённый интеграл вычислим заменой переменной интегрирования.

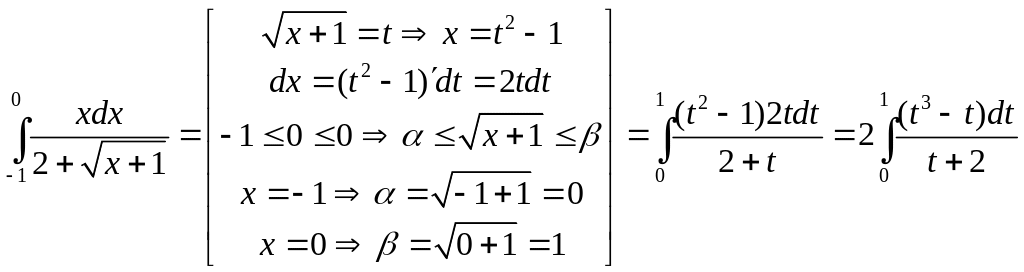
Последний интеграл вычисляем также заменой переменной.

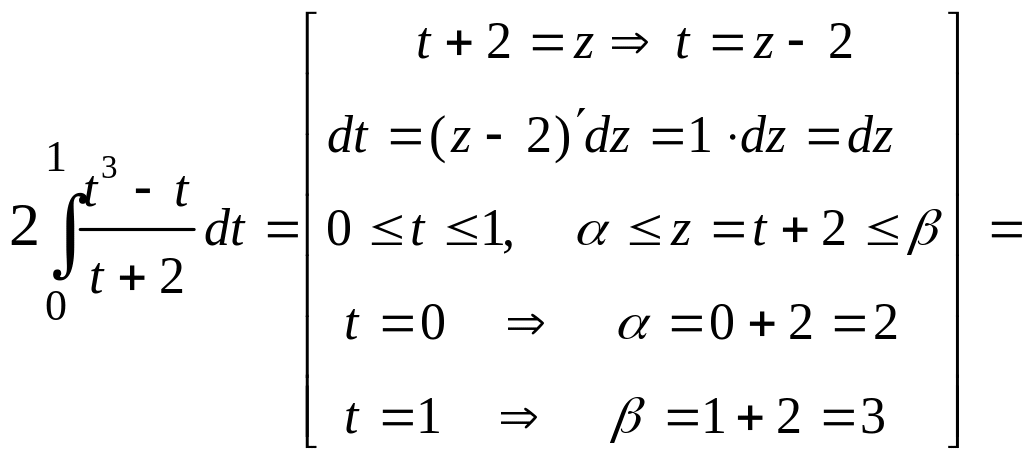
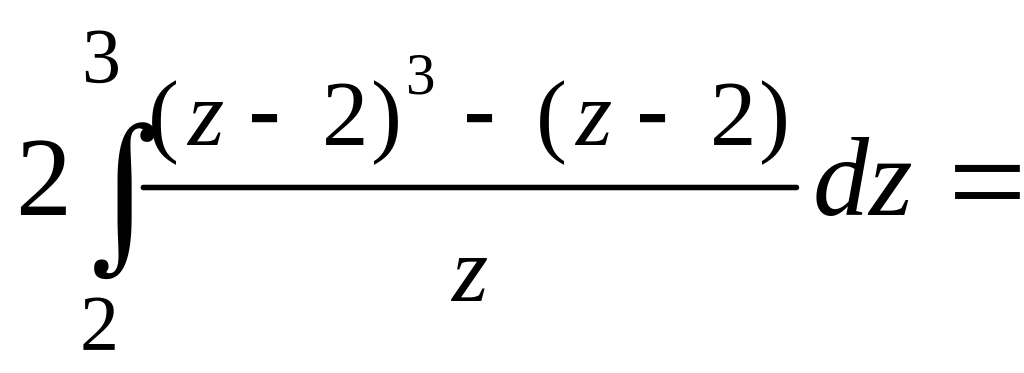
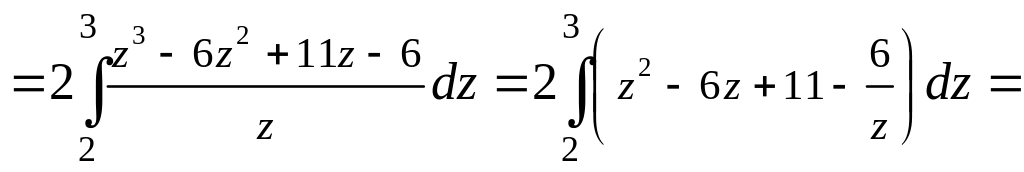
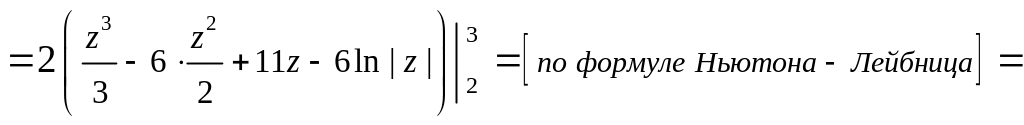
. Ответ: .

б) По определению несобственного интеграла имеем . Определенный интеграл, стоящий под знаком предела, вычислим методом замены переменной: 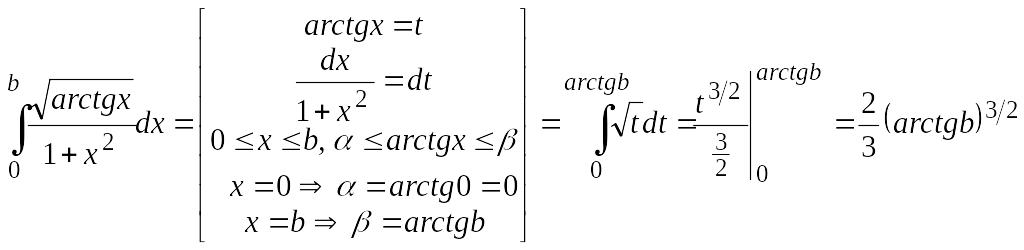Тогда .

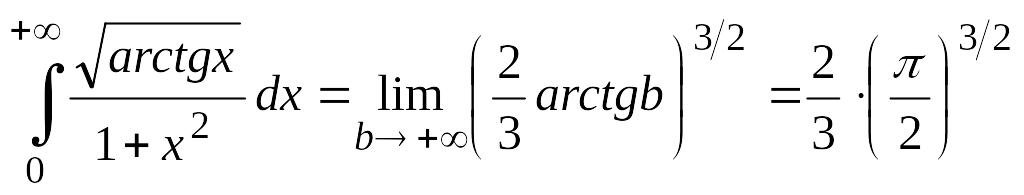Ответ: Несобственный интеграл сходится и равен .

121-130. Вычислить площадь фигуры, ограниченной графиками указанных функций:

Площадь фигуры , где - непрерывные на отрезке функции, задаваемые одним аналитическим выражением, вычисляется по формуле: .

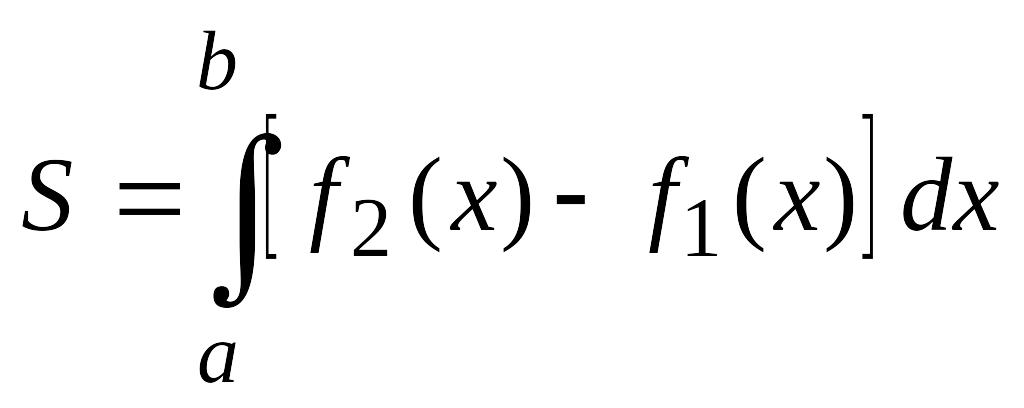Площадь фигуры где - непрерывные на отрезке функции, задаваемые одним аналитическим выражением, вычисляется по формуле: .

Решение.

1) Изобразим фигуру :

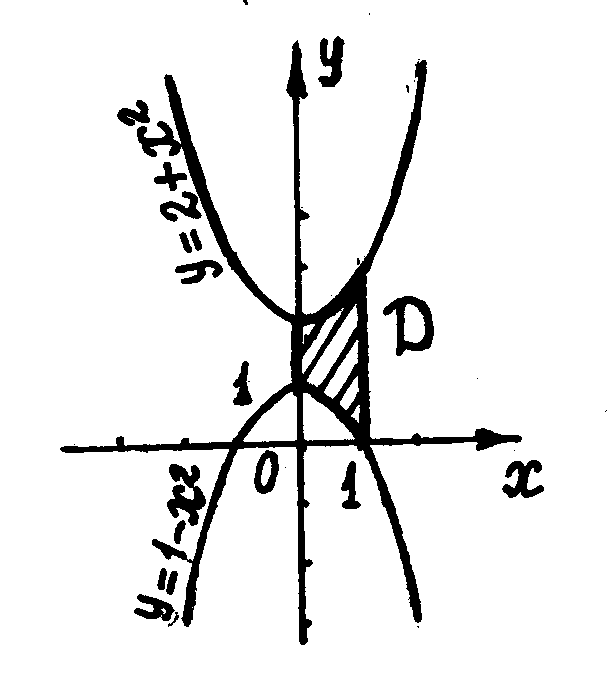
2) Представим в виде .

Если или , то фигуру прямыми, параллельными осям координат, разбивают на части, такие, чтобы они имели вид или . При этом площадь фигуры находят как сумму площадей её частей.

3) Вычислим площадь:

.

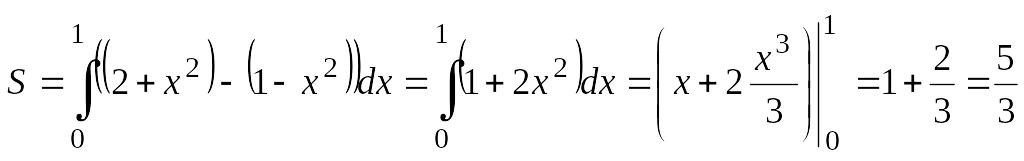Ответ: .