1) Эллипс; 2) окружность; 3) параболу;

4. Если и , то произведение

1) 2; 2) -1; 3) -2;

5. Если и , то частное

1) ; 2) ; 3) ;

6. Если комплексное число , то

1) ; 2) ;

3) ;

III. Решение типовых примеров Типовые примеры к практическому занятию № 1

1. Умножить матрицы , .

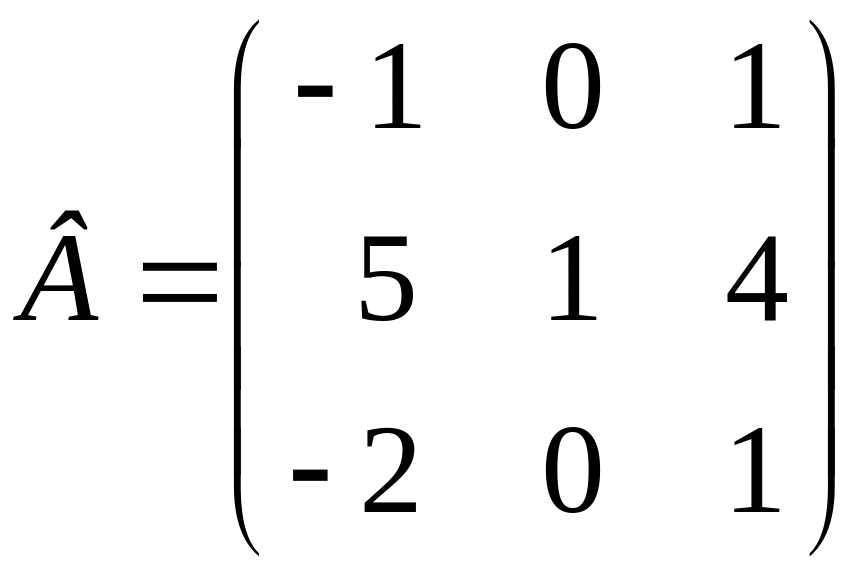Решение. Умножение матриц и определено, если число столбцов первой матрицы равно числу строк второй.

В нашем случае размер – это (23), а размер – это (33), поэтому умножение возможно; размерность результирующей матрицы – это (23). Для того чтобы получить элемент, стоящий на пересечении –й строки и –го столбца новой матрицы, нужно элементы –й строки первой матрицы умножить на соответствующие элементы –го столбца второй матрицы и результат сложить, т.е. элементы матрицы вычисляются по формуле

;

.

2. Вычислить определитель 3-го порядка: .

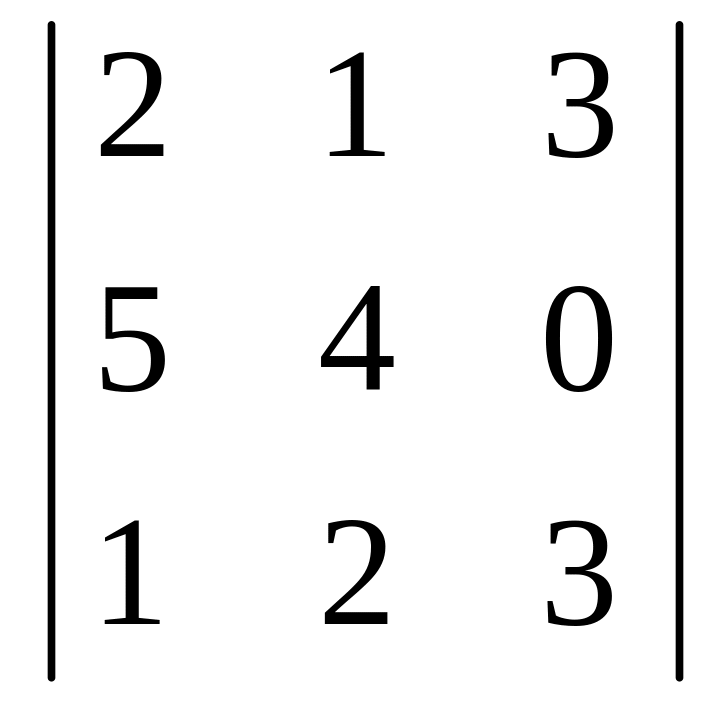Решение. Метод разложения по элементам строки (столбца). С помощью него вычисляют определители любого порядка. Строку (столбец), по элементам которой производится разложение, выбирают так, чтобы в ней содержалось наибольшее количество нулей.

Разложим определитель по элементам какой-либо строки или столбца. Например, выберем для разложения третий столбец. Пусть , , – алгебраические дополнения элементов матрицы , , , соответственно.

В общем случае для элемента алгебраические дополнения находятся по формуле . Минор - определитель, получаемый из исходного вычеркиванием –й строки и –го столбца, на пересечении которых стоит данный элемент. Для нахождения вычеркивается 1-я строка и 3-й столбец .

Аналогично определяем , вычеркивая 2-ю строку и 3-й столбец; получается вычеркиванием 3-й строки и 3-го столбца

. Тогда алгебраические дополнения будут равны ;

Следовательно, определитель = 3∙6 + 3∙3 = 27.

Решение. Метод Саррюса. С помощью этого метода можно вычислять только определители третьего порядка. Сначала к исходному определителю справа приписываем первый и второй столбцы . Тогда определитель равен сумме произведений элементов, стоящих на главной диагонали и диагоналях, параллельных ей, взятых со своими знаками, и произведению элементов побочной диагонали и параллельных ей диагоналях, взятых с противоположными знаками.

3. Найти матрицу, обратную матрице и сделать проверку.

Решение. а) сначала вычислим определитель исходной матрицы

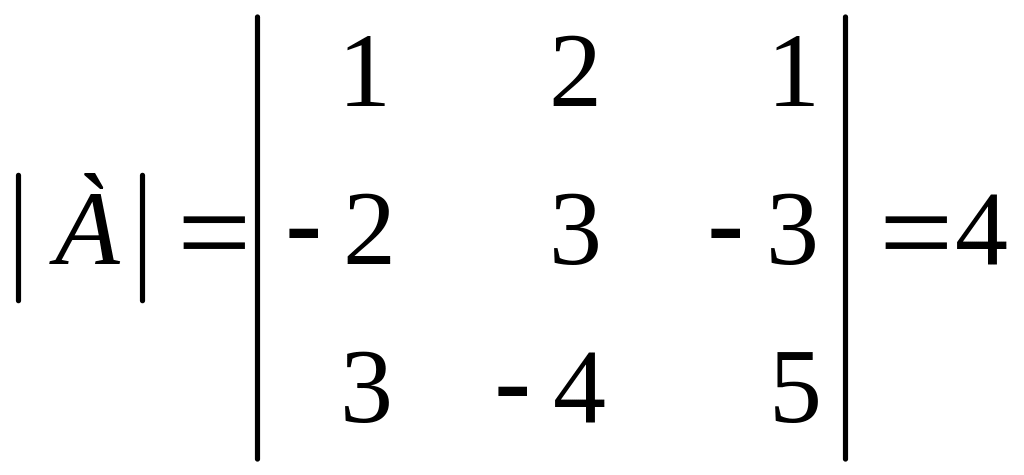. Так как определитель матрицы не равен нулю, то для нее существует обратная матрица .

b) Найдем транспонированную матрицу , которая получается из исходной заменой элементов строк элементами столбцов с сохранением порядка .

с) Найдем алгебраические дополнения всех элементов транспонированной матрицы и составим из них матрицу ̃, которая называется присоединенной (или взаимной):

, ,

, , , , , , . .

d) Вычисляем ,

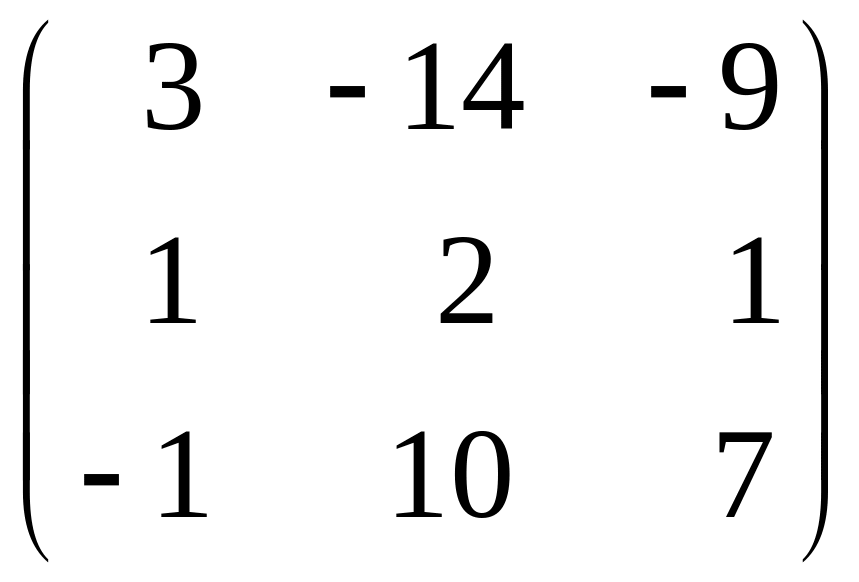
е) Проверим правильность нахождения обратной матрицы : при умножении на исходную матрицу, должна получиться единичная матрица .

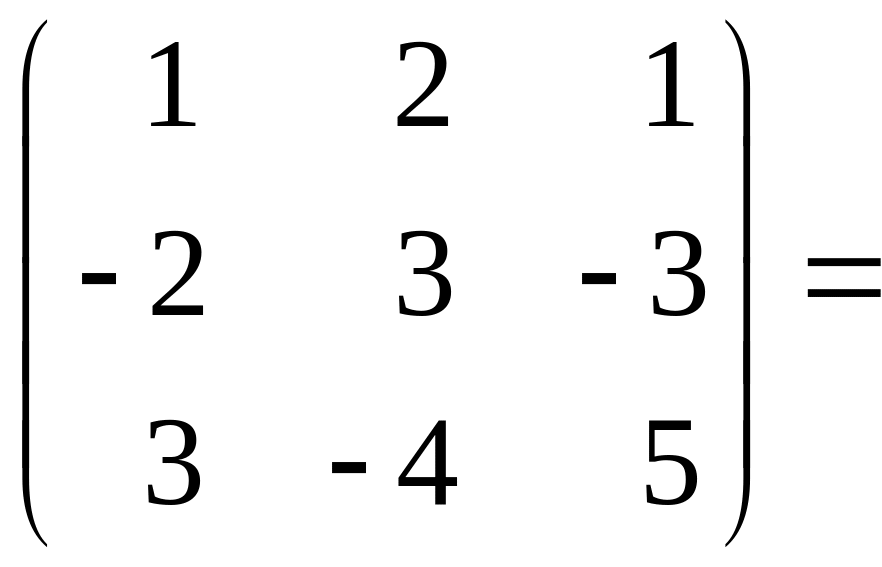
4. Найти ранг следующих матриц

.

Решение. Ранг матрицы – это наивысший порядок отличного от нуля минора. Вычислим минор третьего порядка матрицы

.

Минор третьего порядка отличен от нуля, следовательно, ранг матрицы равен трем.

Вычислим минор третьего порядка матрицы

Минор третьего порядка матрицы равен нулю, значит ранг матрицы не больше, чем два. Так как существует ненулевой минор второго порядка , то ранг матрицы равен двум.