
- •Оглавление Линейная алгебра с элементами аналитической геометрии
- •I. Практические занятия
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 3 “Элементы векторной алгебры” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 4 “Аналитическая геометрия” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •II. Тесты
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Тест № 2
- •Вариант № 1
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 2
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 3
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 4
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 5
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 1
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 2
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 3
- •1) Эллипс; 2) параболу; 3) гиперболу;
- •Вариант № 4
- •1) Эллипс; 2) окружность; 3) гиперболу;
- •Вариант № 5
- •1) Эллипс; 2) окружность; 3) параболу;
- •III. Решение типовых примеров Типовые примеры к практическому занятию № 1
- •Типовые примеры к практическому занятию № 2
- •Решение. Умножим слева обе части уравнения на , а справа – на . Тогда . В результате получаем решение системы . Теперь следует определить обратные матрицы:
- •Типовые примеры к практическому занятию № 3
- •Типовые примеры к практическому занятию № 4
- •Типовые примеры к практическому занятию № 5
- •Литература
- •420108, Г. Казань, ул. Зайцева, д. 17.
Типовые примеры к практическому занятию № 4
1.
Составить
уравнение прямой, проходящей через
точки
![]() и
и
![]() .
Привести уравнение: а) к каноническому
виду; б) к параметрическому виду; в) к
уравнению в отрезках.
.
Привести уравнение: а) к каноническому
виду; б) к параметрическому виду; в) к
уравнению в отрезках.
Решение.
Уравнение прямой,
проходящей через точки
![]() и
и
![]() имеет вид:
имеет вид:
 .
.
Подставив в это
соотношение координаты точек
и
,
получим уравнение прямой
![]() в следующим виде
в следующим виде
![]() .
.
На основе построенного уравнения составим:
а) каноническое
уравнение прямой
![]() ;
;
б) параметрическое
уравнение прямой
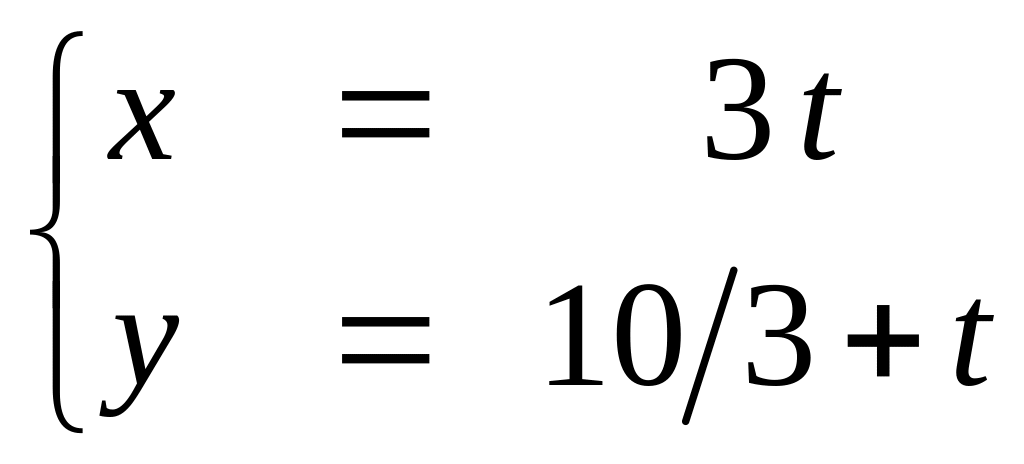 ;
;
в) уравнение прямой
в отрезках:
 .
.
2.
Составить
уравнение прямой, проходящей через
точку
![]() ,
параллельную прямой
,
параллельную прямой
![]() .
.
Решение.
Уравнение прямой,
параллельной заданной прямой
можно записать в виде
![]() ,
где
,
где
![]() неизвестный параметр. Подставив
координаты точки
неизвестный параметр. Подставив
координаты точки
![]() в последнее уравнение
в последнее уравнение
![]() ,
найдем
,
найдем
![]() .
Итак, искомое уравнение прямой имеет
вид:
.
Итак, искомое уравнение прямой имеет
вид:
![]() .
.
3.
На прямой
![]() найти точку, равноудаленную от точек
и
найти точку, равноудаленную от точек
и
![]() .
.
Решение. Напомним,
что расстояние между точками
![]() и
и
![]() определяется по формуле
определяется по формуле
![]() .
.
Выберем на прямой
точку
![]() c
абсциссой
c
абсциссой
![]() .
Тогда ордината этой точки равна
.
Тогда ордината этой точки равна
![]() .
.
Вычислим расстояния
![]()
![]() ,
,
![]() .
.
Так как точка
равноудалена от точек
и
,
то
![]() ,
т.е.
,
т.е.
![]()
![]() .
После преобразований получаем следующее
соотношение
.
После преобразований получаем следующее
соотношение
![]() .
Следовательно,
.
Следовательно,
![]() ;
;
![]() .
Точка
.
Точка
![]() равноудалена от точек
и
.
равноудалена от точек
и
.
4.
Известны координаты вершин треугольника
![]() ,
,
![]() и
и
![]() .
Вычислить площадь и периметр треугольника.
.
Вычислить площадь и периметр треугольника.
Решение.
Составим уравнение прямой, проходящей через точки ,
![]() или
.
или
.
Запишем уравнение
прямой, проходящей через точку
![]() ,
перпендикулярно прямой
.
Известно, что две прямые
,
перпендикулярно прямой
.
Известно, что две прямые
![]() и
и
![]() перпендикулярны, если
перпендикулярны, если
![]() .
.
Поэтому, искомую
прямую запишем в виде
![]() .
Неизвестный параметр найдем, подставив
в это уравнение координаты точки
.
В результате получаем уравнение
.
Неизвестный параметр найдем, подставив
в это уравнение координаты точки
.
В результате получаем уравнение
![]() ,
решение которого
,
решение которого
![]() .
.
Обозначим через точку пересечения этой прямой и прямой . Найдем координаты точки , решив систему уравнений
 ,
,
![]() ;
;
![]() – решение системы.
– решение системы.
Теперь определим
длины
![]()
![]() ,
,
![]() .
.
и вычислим площадь
треугольника
![]() :
:
![]() ;
;
и периметр треугольника :
![]() .
.
Типовые примеры к практическому занятию № 5
1.
Записать комплексное число
![]() в тригонометрической и показательной
формах.
в тригонометрической и показательной
формах.
Решение. Полагаем
![]() .
Вычислим модуль комплексного числа
.
Вычислим модуль комплексного числа
![]() .
.
На основе соотношения
![]() вычислим
– аргумент комплексного числа
вычислим
– аргумент комплексного числа
 .
Теперь можно записать комплексное число
в тригонометрической форме
.
Теперь можно записать комплексное число
в тригонометрической форме
![]() ,
,
![]() .
.
Используя формулу Эйлера, переходим к показательной форме комплексного числа:
![]() ,
,
![]()
2.
Выполнить деление комплексных чисел
![]() .
.
Решение.

3.
Вычислить
![]() .
.
Решение. Полагаем . Запишем данное комплексное число в тригонометрической форме (см. пример 1).
,
Далее применим формулу Муавра
![]()
![]()
4.
Вычислить
![]() .
.
Решение. Полагаем
![]() .
Запишем данное комплексное число в
тригонометрической форме (см. пример
1).
.
Запишем данное комплексное число в
тригонометрической форме (см. пример
1).
,
![]()
Далее применим формулу
![]() ,
,
![]()
![]() ,
,
![]()
При
![]() имеем
имеем
![]()
При
![]() имеем
имеем
![]()
Таким образом,
![]() .
.
Литература
Высшая математика для экономистов: Учебник для вузов / Под ред. Н.Ш.Кремера и др. – М.: ЮНИТИ, 2003. – 471 с.
Общий курс высшей математики для экономистов / Под ред. В.И.Ермакова – М.: ИНФРА-М, 2004. – 656 с.
Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Учебник: в 2-х частях. Ч.1. – М.: Финансы и статистика, 1999. – 224с.
Подписано в печать 30.01.06. Формат 60х90 1/16
Гарнитура Times ET, 10. Усл. печ. л. – 3,8.
Тираж 200 экз.
Типография «Таглимат» ИЭУиП,
лицензия № 172 от 12.09.96 г.
