
- •Оглавление Линейная алгебра с элементами аналитической геометрии
- •I. Практические занятия
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 3 “Элементы векторной алгебры” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 4 “Аналитическая геометрия” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •II. Тесты
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Тест № 2
- •Вариант № 1
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 2
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 3
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 4
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 5
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 1
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 2
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 3
- •1) Эллипс; 2) параболу; 3) гиперболу;
- •Вариант № 4
- •1) Эллипс; 2) окружность; 3) гиперболу;
- •Вариант № 5
- •1) Эллипс; 2) окружность; 3) параболу;
- •III. Решение типовых примеров Типовые примеры к практическому занятию № 1
- •Типовые примеры к практическому занятию № 2
- •Решение. Умножим слева обе части уравнения на , а справа – на . Тогда . В результате получаем решение системы . Теперь следует определить обратные матрицы:
- •Типовые примеры к практическому занятию № 3
- •Типовые примеры к практическому занятию № 4
- •Типовые примеры к практическому занятию № 5
- •Литература
- •420108, Г. Казань, ул. Зайцева, д. 17.
Решение. Умножим слева обе части уравнения на , а справа – на . Тогда . В результате получаем решение системы . Теперь следует определить обратные матрицы:
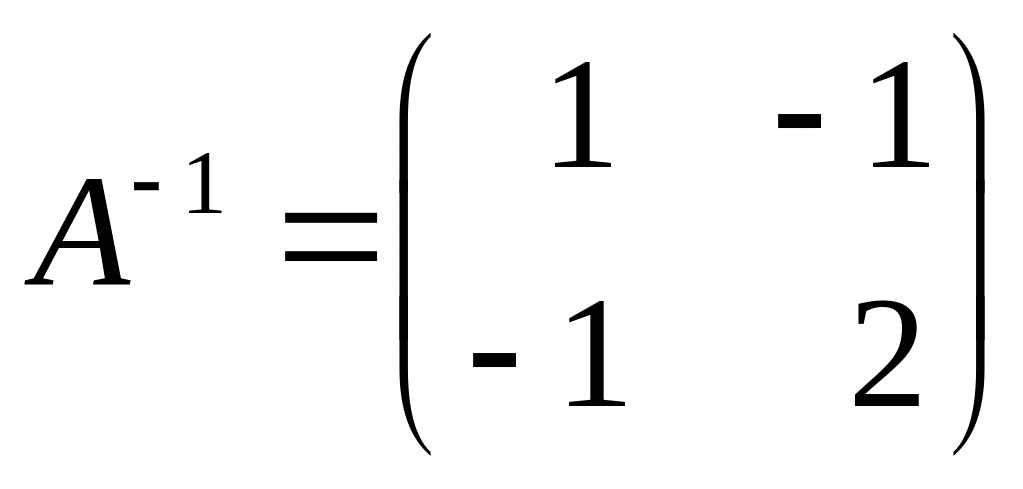 ,
,

и использовать их
в полученной формуле:

Типовые примеры к практическому занятию № 3
1. Даны
векторы:
![]() ;
;
![]() .
.
a) Записать разложение этих векторов по ортам координатных осей.
Решение.
Если
![]() ,
то разложение вектора
,
то разложение вектора
![]() по ортам координатных осей имеет вид:
по ортам координатных осей имеет вид:
![]() .
.
Поэтому:
![]() ,
,
![]() .
.
б) Найти векторы ; и их модули (длину) , .
Решение.
![]()
![]() ;
;
![]() .
.
Учитывая, что
модуль вектора
![]() вычисляется по формуле
вычисляется по формуле
![]() ,
получаем
,
получаем
![]()
![]() .
.
в) Найти скалярный квадрат вектора , т.е.
Решение. Скалярный
квадрат вектора равен квадрату модуля
этого вектора
![]() .
.
г) Найти скалярное произведение .
Решение.
Скалярное
произведение векторов
![]() и
и
![]() определяется по формуле
определяется по формуле
![]() .
.
Поэтому
![]() .
.
д) Найти угол между векторами и .
Решение. Пусть
![]() обозначает угол между векторами
и
.
Тогда
обозначает угол между векторами
и
.
Тогда
 .
.
2. В
базисе
заданы векторы
![]() ,
,
![]() ,
,
![]() .
Установить, что они образуют базис.
.
Установить, что они образуют базис.
Решение. В n-мерном векторном пространстве, n векторов образуют базис, если они являются линейно независимыми. Составим матрицу из этих векторов и вычислим ее определитель:

Он не равен нулю, следовательно, векторы , , образуют базис.
3.
а) Линейный
оператор
в базисе
задан матрицей
 .
Найти образ
,
если
.
Найти образ
,
если
![]() .
.
Решение.
Если оператор
![]() задан матрицей
,
то образ
является произведением матрицы
и вектора
задан матрицей
,
то образ
является произведением матрицы
и вектора
![]() :
:

4. Найти собственные значения и собственные векторы матицы
 .
Провести
нормирование собственных векторов.
Привести матрицу к диагональному виду.
.
Провести
нормирование собственных векторов.
Привести матрицу к диагональному виду.
Решение. Пусть
единичная матрица. Составим
характеристическое уравнение
 ,
,
![]() .
.
Решением уравнения
являются собственные значения линейного
оператора
![]() и
и
![]() .
.
Теперь найдем
собственный вектор
![]() ,
соответствующий собственному значению
.
Для этого решим матричное уравнение
,
соответствующий собственному значению
.
Для этого решим матричное уравнение
![]() или
или
 .
.
Оно сводится к
одному уравнению
![]() .
Положим в нем
.
Положим в нем
![]() ,
(
,
(![]() – число, не равное нулю). Тогда
– число, не равное нулю). Тогда
![]() .
В результате получаем первый собственный
вектор
.
В результате получаем первый собственный
вектор
 .
.
Аналогичным
образом, получаем второй собственный
вектор
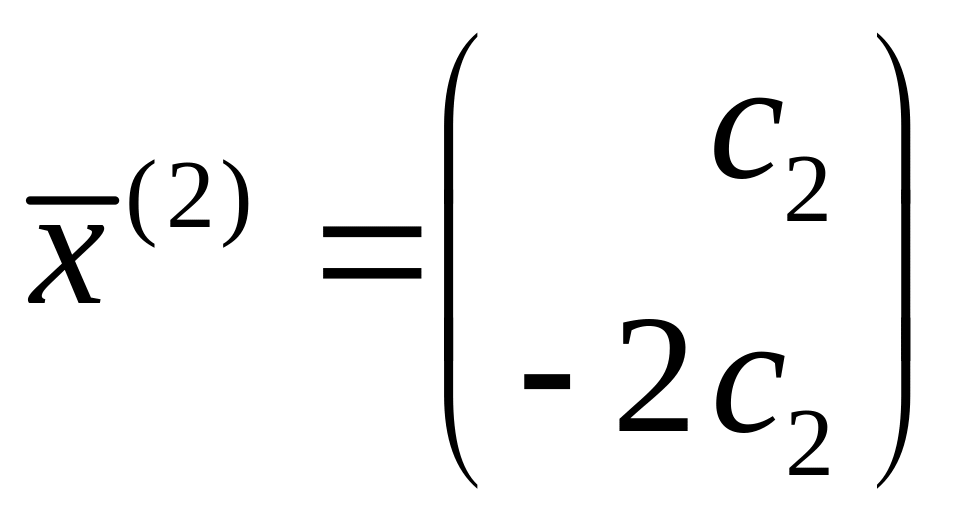 ,
соответствующий собственному значению
.
,
соответствующий собственному значению
.
Осуществим
нормирование векторов
и
![]() .
Для этого найдем модули этих векторов
и разделим каждую компоненту
соответствующего вектора на модуль. В
результате получаем
.
Для этого найдем модули этих векторов
и разделим каждую компоненту
соответствующего вектора на модуль. В
результате получаем
 ,
,
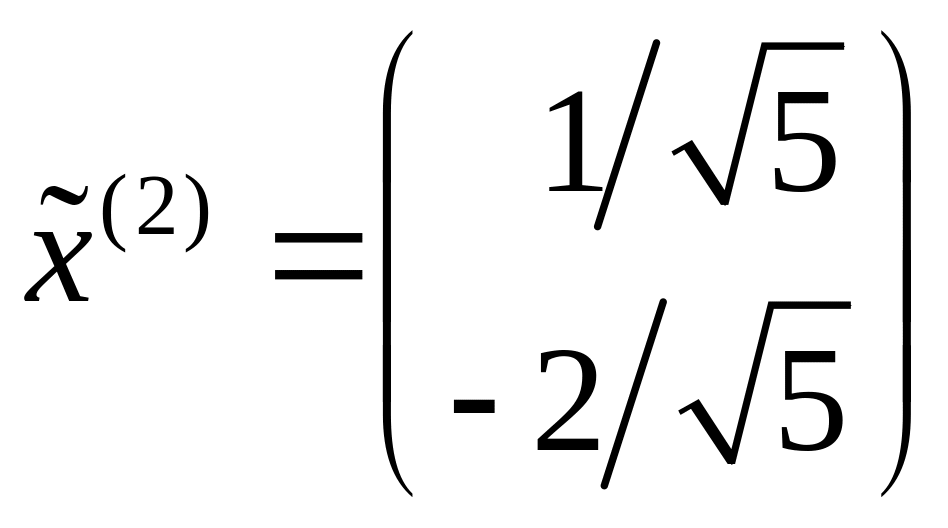 .
.
Таким образом, в базисе, состоящем из любых пар собственных векторов, матрица будет иметь диагональный вид
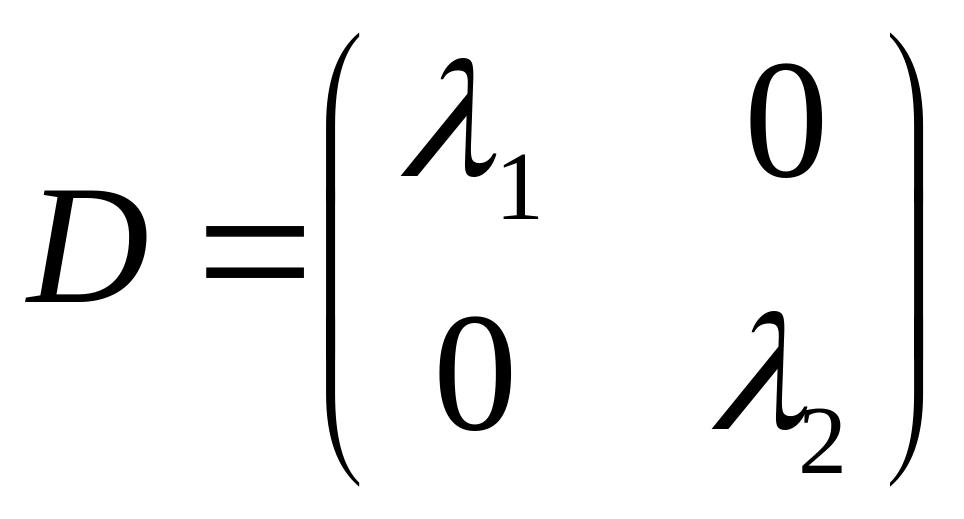 или
или
 .
.
5. Квадратичную форму
![]()
записать в матричном виде.
Решение. Запишем квадратичную форму
![]()
в матричном виде

и используем это выражение для представления заданной формы
 .
.
6.
Привести
квадратичную форму
![]() к каноническому виду; записать
соответствующее преобразование
к каноническому виду; записать
соответствующее преобразование
![]() .
.
Решение. Выделяя полный квадрат, приведем квадратичную форму к каноническому виду:
![]()
![]()
![]()
Обозначим
 ,
тогда
,
тогда
![]() .
.
Преобразуя систему,
получаем
 .
Таким образом, матрицу преобразования,
приводящую квадратичную форму
.
Таким образом, матрицу преобразования,
приводящую квадратичную форму
![]() к каноническому виду, можно записать
так
к каноническому виду, можно записать
так
 .
.
7. Определить,
является ли положительно определенной
квадратичная форма
![]() .
.
Решение. Запишем
матрицу коэффициентов, соответствующую
данной квадратичной форме
 .
Вычислим главные миноры матрицы:
.
Вычислим главные миноры матрицы:
![]() ,
,
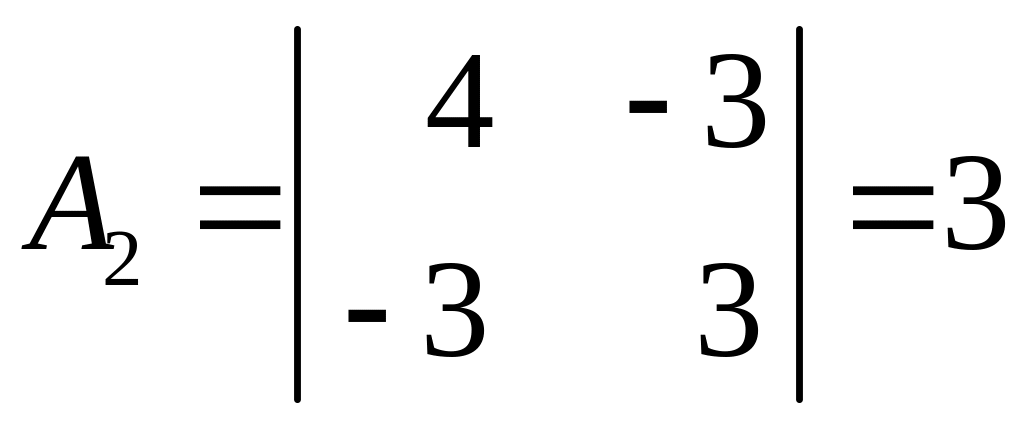 ,
,
 .
.
Все главные миноры матрицы больше нуля. Следовательно, квадратичная форма является положительно определенной.
