
- •Оглавление Линейная алгебра с элементами аналитической геометрии
- •I. Практические занятия
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 3 “Элементы векторной алгебры” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 4 “Аналитическая геометрия” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •II. Тесты
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Тест № 2
- •Вариант № 1
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 2
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 3
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 4
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 5
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 1
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 2
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 3
- •1) Эллипс; 2) параболу; 3) гиперболу;
- •Вариант № 4
- •1) Эллипс; 2) окружность; 3) гиперболу;
- •Вариант № 5
- •1) Эллипс; 2) окружность; 3) параболу;
- •III. Решение типовых примеров Типовые примеры к практическому занятию № 1
- •Типовые примеры к практическому занятию № 2
- •Решение. Умножим слева обе части уравнения на , а справа – на . Тогда . В результате получаем решение системы . Теперь следует определить обратные матрицы:
- •Типовые примеры к практическому занятию № 3
- •Типовые примеры к практическому занятию № 4
- •Типовые примеры к практическому занятию № 5
- •Литература
- •420108, Г. Казань, ул. Зайцева, д. 17.
Типовые примеры к практическому занятию № 2
1. Решить систему линейных уравнений

Решение. Метод
обратной матрицы. Запишем систему в
матричном виде. Для этого обозначим
матрицу системы
(она состоит из коэффициентов при
переменных); столбец неизвестных ,
столбец свободных членов
,
столбец свободных членов
 ,
состоящий из правых частей уравнений.
Тогда система представима в матричном
виде:
.
,
состоящий из правых частей уравнений.
Тогда система представима в матричном
виде:
.
Для нахождения
![]() умножим матричное уравнение на
слева:
умножим матричное уравнение на
слева:
![]() .
Найдем матрицу
.
Найдем матрицу
![]()

Тогда столбец неизвестных:




![]()
Решение. Метод
Крамера. Пусть
![]() - определитель матрицы
:
- определитель матрицы
:
 .
Так как определитель не равен нулю, то
можно использовать метод Крамера;
система имеет единственное решение.
.
Так как определитель не равен нулю, то
можно использовать метод Крамера;
система имеет единственное решение.
Определитель
![]() получаем из определителя
заменой первого столбца на столбец
свободных членов
,
а остальные столбцы остаются прежними:
получаем из определителя
заменой первого столбца на столбец
свободных членов
,
а остальные столбцы остаются прежними:
 .
Аналогично, заменяя в исходном определителе
второй, а затем третий столбцы на столбец
свободных членов, получим соответственно
.
Аналогично, заменяя в исходном определителе
второй, а затем третий столбцы на столбец
свободных членов, получим соответственно
![]() и
и
![]() .
.
 ,
,

Теперь воспользуемся
формулой Крамера и найдем все переменные:
![]() ,
,
![]() ,
,
![]() .
.
Решение. Метод Гаусса. Метод Гаусса – это универсальный метод решения систем линейных уравнений. Он заключается в последовательном исключении переменных.
Составим расширенную
матрицу системы, включающую в себя
матрицу системы и столбец свободных
членов
 .
.
Произведем элементарные преобразования со строками матрицы, приведя ее к треугольному виду, т.е. к матрице, в которой все элементы, ниже главной диагонали равны нулю (при этом диагональные элементы не равны нулю).
Шаг 1. Если в матрице
элемент
![]() ,
то перестановкой строк нужно добиться,
чтобы элемент
,
то перестановкой строк нужно добиться,
чтобы элемент
![]() .
В нашем примере
.
.
В нашем примере
.
Сначала обнулим
элементы первого столбца ниже главной
диагонали. Для этого сначала умножим
элементы первой строки на число
 и прибавим к элементам второй строки.
Затем умножим элементы первой строки
на число
и прибавим к элементам второй строки.
Затем умножим элементы первой строки
на число
 и прибавим к элементам третьей строки:
и прибавим к элементам третьей строки:

 →
→
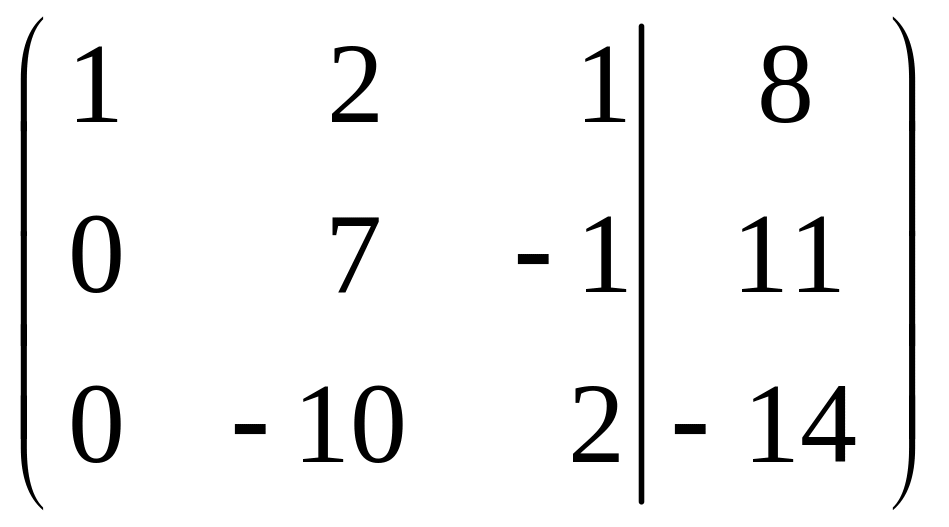
Шаг 2. Если в
полученной матрице
![]() ,
то обнулим элемент второго столбца ниже
главной диагонали. Для этого умножим
вторую строку на число
,
то обнулим элемент второго столбца ниже
главной диагонали. Для этого умножим
вторую строку на число
 и прибавим к третьей строке:
и прибавим к третьей строке:
 →
→

Полученной треугольной матрице соответствует система уравнений
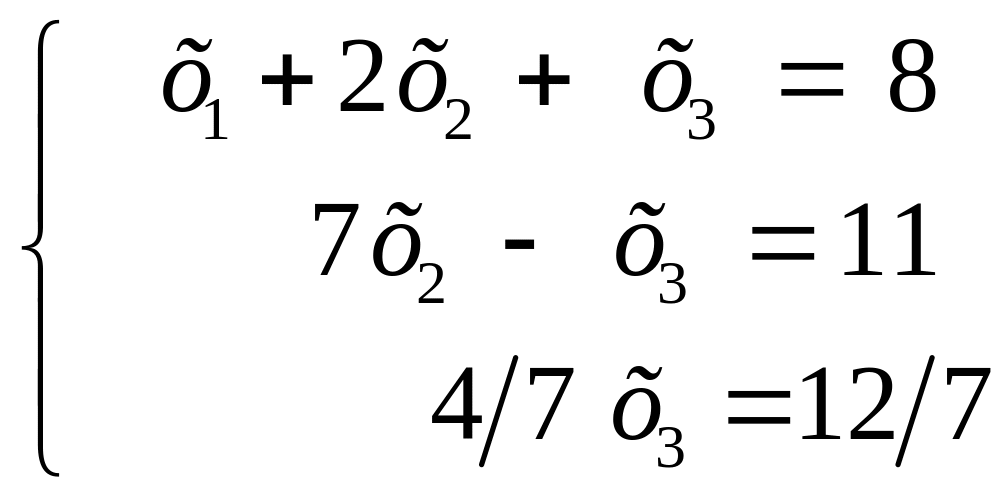 .
.
Из третьего
уравнения системы вычисляем
![]() ;
из второго
;
из второго
![]() ;
из первого
;
из первого
![]() .
.
2. Найти базисное решение системы уравнений

Решение. Преобразуем расширенную матрицу системы

Следовательно, ранг матрицы системы равен двум и система является неопределенной.
Определитель из
коэффициентов при переменных
![]() отличен от нуля:
отличен от нуля:
 .
Поэтому их можно выбрать в качестве
основных (базисных). Оставляя их в левой
части, переменную
.
Поэтому их можно выбрать в качестве
основных (базисных). Оставляя их в левой
части, переменную
![]() перенесем в правую часть. В результате
получим систему
перенесем в правую часть. В результате
получим систему

Решение этой системы зависит от переменной

Придавая переменной
произвольное значение
![]() ,
получим общее решение системы:
,
получим общее решение системы:
![]()

Полагая
![]() ,
найдем одно из базисных решений
,
найдем одно из базисных решений
![]()
3. Решить систему линейных однородных уравнений. Найти фундаментальную систему решений.

Решение. Преобразуем матрицу системы


Выберем
![]() ,
,
![]() в качестве базисных переменных и решим
систему
в качестве базисных переменных и решим
систему

![]()
Полагая
![]() и
и
![]() ,
получим общее решение системы
,
получим общее решение системы
![]()

Из общего решения выделим два частных решения:
1) пусть
![]() ,
,
![]() ,
тогда
,
тогда

2) пусть
![]() ,
,
![]() ,
тогда
,
тогда
![]()
Они образуют фундаментальную систему решений
![]()
4. Решить матричное уравнение где


 .
.
