
- •Тема III – основы математического анализа
- •§8. Множества и операции над ними
- •8.1. Основные понятия
- •8.2. Числовые множества
- •9. Функция
- •9.1. Понятия функции и ее графика
- •9.2. Способы задания функций
- •9.3. Некоторые свойства функций
- •9.4. Обратная функция
- •9.5. Основные элементарные функции
- •9.5. Сложная функция и элементарные функции
- •§10. Предел функции
- •10.1. Предел функции в точке
- •10.2. Односторонние пределы
- •10.3. Предел функции на бесконечности
- •10.4. Бесконечно большие функции
- •§11. Бесконечно малые функции
- •11.1. Определение и основные теоремы
- •11.2. Основные теоремы о пределах
- •11.3. Техника вычисления пределов. Примеры
- •11.4. Первый замечательный предел
- •11.5. Эквивалентные функции
- •11.6. Второй замечательный предел
- •11.7. Техника вычисления пределов вида .
- •§12. Непрерывность функции
- •12.1. Непрерывность функции в точке и в области
- •12.2. Основные теоремы о непрерывных функциях
- •12.3. Классификация точек разрыва
- •§13. Производная функции
- •13.1. Приращение аргумента и приращение функции
- •13.2. Определение производной функции в точке
- •13.3. Геометрический смысл производной
- •13.4. Физический смысл производной
- •13.5. Дифференцируемость функций
- •13.6. Производная постоянной, суммы, произведения и частного двух функций
- •13.7. Производная сложной и обратной функции
- •13.8. Производные основных элементарных функций
- •13.9. Производная функции, заданной неявно
- •13.10. Логарифмическая производная
- •13.11. Производная функции, заданной параметрически
- •13.13. Примеры вычисления производных
- •13.14. Производные высших порядков
- •§14. Дифференциал функции
- •14.1. Понятие дифференциала функции
- •14.2. Основные теоремы о дифференциалах
- •14.3. Применение дифференциала к приближенным вычислениям
- •§15. Исследование функций при помощи производных
- •15.1. Правило Лопиталя
- •15.2. Некоторые теоремы о дифференцируемых функциях
- •15.3. Исследование поведения функций и построение графиков
- •Общее исследование функции и построение ее графика рекомендуется выполнять по следующей схеме:
12.2. Основные теоремы о непрерывных функциях
Теорема 12.1. Сумма, произведение и частное двух непрерывных функций есть непрерывная функция (для частного за исключением тех значений аргумента, в которых знаменатель равен нулю)
Теорема
12.2.
Пусть функция
![]() непрерывна в точке х0,
а функция
непрерывна
в точке
непрерывна в точке х0,
а функция
непрерывна
в точке
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() непрерывна
в точке х0.
непрерывна
в точке х0.
Теорема 12.3. Функция, обратная для непрерывной монотонной функции также непрерывна и монотонна.
Теорема 12.4 (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Т еорема
12.5
(Больцано-Коши). Если функция
непрерывна
на отрезке [a,
b]
и принимает на его концах неравные
значения f(a)=A,
F(b)=B,
то на этом отрезке она принимает все
промежуточные значения между A
и B.
еорема
12.5
(Больцано-Коши). Если функция
непрерывна
на отрезке [a,
b]
и принимает на его концах неравные
значения f(a)=A,
F(b)=B,
то на этом отрезке она принимает все
промежуточные значения между A
и B.
12.3. Классификация точек разрыва
Пусть точка разрыва функции .
Точка называется точкой устранимого разрыва первого рода, если
 .
.

Точка называется точкой неустранимого разрыва первого рода, если
 ,
а
,
а
 ,
причем
,
причем
 .
.
Точка называется точкой разрыва второго рода, если хотя бы один из односторонних пределов (справа или слева) не существует или равен бесконечности.


![]()

§13. Производная функции
13.1. Приращение аргумента и приращение функции
Рассмотрим
функцию
![]() .
Пусть x
– некоторое значение аргумента,
– соответствующее значение функции.
Перейдем от значения x
к другому значению аргумента x1.
Разность x – x1
обозначим через x
и назовем приращением
аргумента.
Значение функции, соответствующее
значению аргумента x1 = x + x,
равно f(x+x).
Разность f(x+x)–f(x)
называется приращением
функции в
точке x,
соответствующим приращению аргумента
x,
и обозначается y:
.
Пусть x
– некоторое значение аргумента,
– соответствующее значение функции.
Перейдем от значения x
к другому значению аргумента x1.
Разность x – x1
обозначим через x
и назовем приращением
аргумента.
Значение функции, соответствующее
значению аргумента x1 = x + x,
равно f(x+x).
Разность f(x+x)–f(x)
называется приращением
функции в
точке x,
соответствующим приращению аргумента
x,
и обозначается y:
y = f(x+x) – f(x).

13.2. Определение производной функции в точке
Пусть функция определена в некоторой окрестности точки x. Дадим аргументу x приращение x (при этом предполагается, что точка x+x принадлежит области определения функции). Тогда функция получит приращение y=f(x+x)–f(x).
Производной функции f(x) в точке x называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
Производная
функции y = f(x)
в точке x
обозначается символами
![]() .
Итак, по определению
.
Итак, по определению
![]() .
.
Как
следует из определения, производная
функции f(x)
в точке x
есть число, зависящее от рассматриваемого
значения x
(но не зависящее от x).
Рассматривая производную функции f(x)
в различных точках x
мы будем получать, вообще говоря,
различные значения. Таким образом,
производная
![]() является функцией переменной x,
определенной в области определения
функции f(x)
или в части этой области.
является функцией переменной x,
определенной в области определения
функции f(x)
или в части этой области.
13.3. Геометрический смысл производной
П усть
имеем кривую и на ней фиксированную
точку
усть
имеем кривую и на ней фиксированную
точку
![]() .
Возьмем на кривой точку
.
Возьмем на кривой точку
![]() и проведем секущую
и проведем секущую
![]() .
Если точка
неограниченно приближается по кривой
к точке
,
то секущая
принимает различные положения. Предельное
положение данной секущей – касательная.
.
Если точка
неограниченно приближается по кривой
к точке
,
то секущая
принимает различные положения. Предельное
положение данной секущей – касательная.
Рассмотрим функцию .
Пусть
![]() ,
,
![]() ,
–
секущая,
,
–
секущая,
![]() .
Если
неограниченно приближается к
,
то
.
Если
неограниченно приближается к
,
то
![]() .
Тогда
.
Тогда
![]() .
.
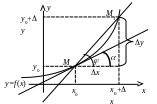
.
Следовательно,
значение
производной
при данном значении аргумента
равняется тангенсу угла, образованного
с положительным направлением оси
![]() касательной к графику функции
в соответствующей точке
.
касательной к графику функции
в соответствующей точке
.
Вспомнив
вид уравнения прямой на плоскости с
угловым коэффициентом, мы можем написать
уравнение
касательной
к графику функции
в точке касания (х0,
у0),
где
![]() :
:
![]()
