matematika_С1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский университет дружбы народов

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

летворяют решения

летворяют решения

.pdf

Скачиваний:

Добавлен:

15.04.2015

Размер:

1.1 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

http://vk.com/ege100ballov

МАТЕМАТИКА ЕГЭ 2011

Отбор корней в тригонометрических уравнениях

(типовые задания С1)

Корянов А. Г. г. Брянск akoryanov@mail.ru

Прокофьев А.А. г. Москва aaprokof@yandex.ru

СОДЕРЖАНИЕ

1.Способы отбора корней в тригонометрических уравнениях.……….. 1

2.Отбор общих корней в нескольких сериях решений тригонометри-

ческого уравнения………………… 1

3. Отбор корней уравнения, удовлетворяющих дополнительным усло-

виям………………………………….. 2

а) корни уравнения принадлежат промежутку……………………... 2

б) корни уравнения удовлетворяют неравенству……………………… 4

4.Отбор корней уравнения, связанный с методом замены……………... 4

5.Уравнения, содержащие дробные выражения…………………………... 5

6.Уравнения, содержащие иррациональные выражения……………. 6

7.Уравнения, содержащие показательные выражения………………… 8

8.Уравнения, содержащие логарифмические выражения…………... 8

9.Уравнения, содержащие модули .. 9

10.Уравнения, содержащие обратные тригонометрические выраже-

ния…………………………………… 10

11.Комбинированные уравнения…. 10

12.Упражнения……………………... 12

Список литературы…………………. 21

1.Способы отбора корней

втригонометрических уравнениях

При отборе корней в процессе реше-

ния тригонометрических уравнений обычно используют один из следующих способов.

● Арифметический способ:

а) непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения; б) перебор значений целочисленного па-

раметра и вычисление корней. ● Алгебраический способ:

а) решение неравенства относительно неизвестного целочисленного параметра и вычисление корней; б) исследование уравнения с двумя цело-

численными параметрами. ● Геометрический способ

а) изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений; б) изображение корней на числовой прямой с последующим отбором с учетом имеющихся ограничений.

2. Отбор общих корней в нескольких сериях решений тригонометрического уравнения

Пример 1. Решить уравнение:

cosxcos5x 0.

Решение. Данное уравнение равносильно совокупности уравнений


cosx 0	x		k
cosx 0	x	2	k
		2				k,n Z
cos5x 0					n
	x
	x	10
		10		5


Рассмотрим уравнение		k			n	.
			10
	2			5
После	преобразований		получаем
n 5k 2.	Следовательно, вторая			серия

решений включает в себя первую серию решений.

Отбор корней удобно проводить на тригонометрической окружности, используя градусную меру полученных решений x 90 k 180 или x 18 n 36 .

http://vk.com/ege100ballov

Ответ: n , n Z . 10 5

Пример 2. Решить уравнение:

cosx cos3x 2.

Решение. Из неравенств cosx 1 и

cos3x 1 следует, что равенство воз-

можно только в том случае, когда оба слагаемых одновременно будут равны 1.

cosx cos3x 2				cosx 1,
cosx cos3x 2
				cos3x 1.
	x 2 n,
		2 k		n, k Z.
		2 k		n, k Z.
	x		,
	x	3	,
		3

Вторая серия решений включает первую серию, поэтому имеем решение системы x 2 n, n Z.

Ответ: 2 n, n Z.

Пример 3. Решить уравнение: sin7x cos4x 1.

Решение. Воспользовавшись формулой преобразования произведения синуса и косинуса в сумму, приводим уравнение к виду sin11x sin3x 2, откуда полу-

чим	sin11x 2 sin3x.		Так как при	лю-
бом	значении	x	sin11x 1,	а
2 sin3x 1,		то	равенство
sin11x 2 sin3x		может выполняться в

том и только в том случае, когда

sin11x 1,

2 sin3x 1
			2 n
x					, n Z,
x	22		11		, n Z,
	22		11
		2 m
		2 m
x	6		3	, m Z.
	6		3

Найдем такие целые значения n и m, при которых решения в полученных се-

риях совпадают		2 n			2 m	,
			6
22	11			3

т.е. 3n 2 11m. Выражая из последнего

равенства n, получаем n 3m 2m 2 . 3

Так как n – целое, то последнее равенство возможно, только если 2m 2 делится на 3, т.е. 2m 2 3k, k Z. Отсюда

m 1 k k . Поскольку m должно быть

2
целым, то k	должно быть четным. Если
k 2p,	где	p Z,	то

m 1 2p 2p 3p 1. Следовательно, 2

x 2 (3p 1) 2 p . 6 3 2

Ответ: 2 p, p Z. 2

3. Отбор корней уравнения, удовлетворяющих дополнительным условиям

а) корни уравнения принадлежат промежутку

Пример 4. Найдите все решения уравнения sin 2x cosx, принадлежащие про-

		3
межутку	;		.
		4

http://vk.com/ege100ballov

Решение. Приведем уравнение к виду

cosx(2sin x 1) 0.									Отсюда											получаем
два уравнения cosx 0													или sin x											1	.
два уравнения cosx 0													или sin x												.
																						2
1) cosx 0,	x				n;								n Z.
1) cosx 0,	x				n;								n Z.
			2														3
	то x																3
Если n 0,							,					;									.
Если n 0,				2			,	2				;									.
				2				2										4
Если n 1, то x					3			,		3										3
														;								.
				2										;								.
				2				2										4
Если n 1, то x																							3
											,					;										.
								2			,					;						4				.
Если n 2, то								2					2									4
Если n 2, то
x		3	,			3									3
													;						.
													;			4			.
	2			2												4

2) sin x 1 ,

x 2 n или x 5 2 n, n Z.

	6								6		3
			0, то x				,				3
Если n										;		или
Если n										;	4	или
						6	6				4
x	5			5		3
		,			;			.
	6	,	6		;	4		.
	6		6			4

Если n 1, то для первой серии решений

x	13					13					3
					,			;					.
						6
	6										4
Если n 1, то
x	11					11				3
			,					;						или
	6					6
											4
x		7					7					3
				,					;					.

	6					6				4

Замечание. Другой вариант отбора корней можно провести на тригонометрическом круге, учитывая, что общий наименьший положительный период функций sin x и cosx, входящих в уравнение, равен 2 .

Ответ:	;		;		.
		2		6
2

Пример 5. Найдите все решения уравнения sin2 2x sin2 3x 1, принадлежащие отрезку [1;2].

Решение. Воспользуемся формулами понижения степени и преобразования суммы функций в произведение

sin2 2x sin2 3x 1

1 cos4x 1 cos6x 1

2 2

cos4x cos6x 0

2cos5xcosx 0

				k
cos5x 0	x
cos5x 0	x	10		5 k Z
		10		5 k Z
cosx 0
	x		k
	x	2	k
		2

x k , k Z (см. Пример 1). 10 5

Решим двойное неравенство

1 k 2 10 2 k 20

105

10 2 k 20


		10					k					20

			2											2
				5		1		k					10				1	.

					2											2
Так как	5		1		5					1				17	,
					3,2
	2								2		16

10 1 10 1 17 и k Z, то k 2.2 3 2 6

Тогда x 2 . 10 5 2

Ответ: . 2

Пример 6. Укажите количество корней уравнения

ctg3x sin 6x cos6x cos12x 0

на промежутке [0;2 ].

Решение. Умножая обе части уравнения

на sin3x 0, получаем

sin3x sin3x cos12x 0,

sin3x(1 cos12x) 0. Отсюда имеем

		n
cos12x 1,	x		,
	x		,
		6		n,k Z
		6		n,k Z
sin3x 0		k
	x	3
		3

Проведем отбор корней, используя тригонометрическую окружность. Для этого полученные значения в серии решений и серии ограничений изобразим на

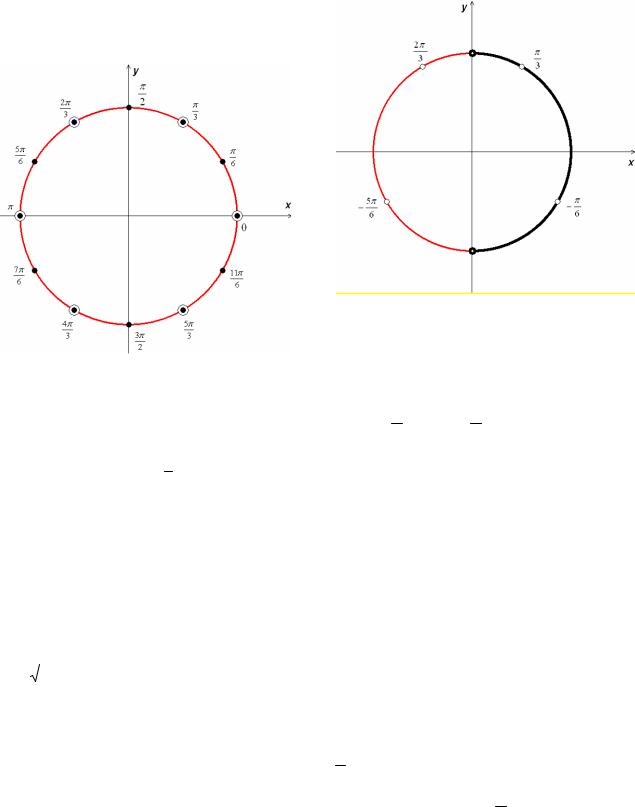
http://vk.com/ege100ballov

тригонометрической окружности и в ответ запишем количество не совпавших в обеих сериях значений переменной х.

Ответ: 6.

б) корни уравнения удовлетворяют неравенству

Пример 7. Найдите все корни уравнения:

(2sin x 1)(2sin x 3) 0,

удовлетворяющие неравенству cosx 0.

Решение. Данное уравнение равносильно совокупности уравнений


				x					2 n
				x			6		2 n
			1				6
sin x							5
				x			5			2 n
				x						2 n
		2					6
		2					6			n,k Z.
	3									n,k Z.
sin x	3			x		2 k
sin x				x		2 k
	2				3
	2				3
				x	2			2 k
				x				2 k
					3
					3

Изобразим полученные решения на тригонометрической окружности. Каждому уравнению соответствуют две точки на тригонометрической окружности. В ответ запишем только решения, расположенные на дуге окружности, соответствующей неравенству cosx 0, т.е. лежащие в I и IV четвертях.

Следовательно, данному условию удов-

Ответ: 2 k; 2 n , n,k Z.

4.Отбор корней уравнения, связанный

сметодом замены

Пример 8. Решить уравнение:

2sin4 x sin2 x 1 0.

Решение.			Обозначим sin2 x t,						где
0 t 1.			Тогда				получим	квадратное
уравнение 2t2					t 1 0, имеющее корни
t1 1 и t2				1			(не удовлетворяет усло-

			2			Для уравнения sin2			x 1
вию 0 t			1).
имеем
	1 cos2x	1;			cos2x 1;			2x 2 n,
2

x n, n Z . 2

Ответ: n, n Z . 2

Пример 9. Решите уравнение:

arccos2 x 8arccosx 15 0.

Решение. Положим arccosx t. Так как множество значений функции arccosx – отрезок 0; , найдем решения уравнения

http://vk.com/ege100ballov

t2 8t 15 0,			удовлетворяющие		усло-
вию	0 t .		Такой корень один: t 3.
Если	t 3,		то	arccosx 3,	откуда
x cos3.				Ответ: cos3.

5. Уравнения, содержащие дробные
		выражения
Пример 10. Решить уравнение:
		cosx		1 sin x.
	1 sin x

Решение. Данное уравнение равносильно системе

	cosx (1 sin x)(1 sin x)

	1 sin x 0
		2	x 0			cosx 0
		2
cosx cos
						cosx 1
sin x 1
						sin x 1

	x			n
	x		2	n
			2		n,k,m Z

	x 2 k

x 2 m2

Для отбора корней используем тригонометрический круг.

Ответ: 2 n;2 k; n,k Z. 2

Пример 11. Решить уравнение:

cos2x cosx 1 0. tgx 1

Решение. Данное уравнение равносильно системе

cos2x cosx 1 0

cosx 0

tgx 1 0

cosx(2cosx 1) 0

cosx 0

tgx 1

		1	x			2 k
		1	x			2 k
cosx		2			3
		2

cosx 0			x		n
cosx 0			x	2	n
	tgx 1			2
	tgx 1

			x		m
			x	4	m
				4

k,m,n Z.

Ответ: 2 k, k Z.

		3
Пример 12. Решите уравнение:
1		1	1.
	sin2 x
		tgx

Решение. Уравнение определено при ус-

ловиях sin x 0			и cosx 0.			Используя
тригонометрические				формулы,			получим
ctg2 x ctgx 0.			Отсюда ctgx 0					или
ctgx 1.		Корни	первого			уравнения
x	n, n Z		не	удовлетворяют				не-

2
равенству		cosx 0.		Решения			второго
уравнения		x	k,		k Z удовлетво-

		4
ряют условиям sin x 0					и cosx 0. Дей-

ствительно, так как число 2 является общим наименьшим положительным пе-

http://vk.com/ege100ballov

риодом функций ctgx, sin x и cosx, то достаточно рассмотреть точки на тригонометрическом круге (сделайте рисунок),

соответствующие		условиям				ctgx 1,
sin x 0	и cosx 0.
	Ответ:		x		k, k Z.

			4			1
Замечание. Замена выражения								на
						sin2
выражение 1 ctg2 x							x
		является				тождест-
венным	преобразованием			при		условии
sin x 0,	а замена	1	на		ctgx может

tgx

привести к появлению посторонних кор-

ней x n, n Z. 2

Пример 13. Решите уравнение:

cosx sin 2x 1. cos3x

Решение. Общий наименьший положительный период функций cosx, cos3x, sin 2x равен 2 . Поэтому достаточно рассмотреть решения уравнения на промежутке [0;2 ).

Умножим обе части уравнения на cos3x 0. Далее получаем

cosx sin 2x cos3x
cos3x cosx sin 2x 0
2sin 2xsin x sin 2x 0
														sin 2x 0,
sin 2x(2sin x 1)								0										1
sin 2x(2sin x 1)								0						sin x				1	.
														sin x					.
																	2
		k
x					,
x		2			,
		2

x						2 l,				k, l, m Z.
x						2 l,				k, l, m Z.
		6
		7
		7				2 m,
x		6				2 m,
		6
На промежутке [0;2 ) содержатся
корни 0,	, ,		3				,	7	,		11			. Из условия
корни 0,	, ,			2			,	6	,	6				. Из условия
2				2				6		6			n
cos3x 0 получаем								x					n		,		n Z, а
cos3x 0 получаем								x		6					,		n Z, а
										6				3
на промежутке						[0;2 )						x				,	x			,
на промежутке						[0;2 )						x				,	x			,
														6			2

x	5	,	x	7	, x	3	, x		11		. Таким
						2
6			6							6
образом,			остались числа 0 и , а значит,
исходное			уравнение			имеет				множество
корней x t,t Z.
						Ответ: t, t Z.
Пример 14. Решите уравнение:
		6sin xcosx sin 2xsin						2		0.
								x

Решение. Воспользуемся формулой синуса двойного аргумента

3sin 2x sin 2xsin				2	0,
3sin 2x sin 2xsin				x	0,
		2		x
		2
sin 2x	3 sin		0.
sin 2x	3 sin		0.
		x

Так как 3 sin 2 0, то последнее x

уравнение равносильно системе

sin 2x 0		k
	x		, k Z, k 0.
		2
x 0,

Ответ: k , k Z, k 0. 2

6. Уравнения, содержащие иррациональные выражения

Пример 15. Решить уравнение:

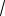5cosx cos2x 2sin x 0.

Решение. Перепишем уравнение в виде

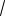5cosx cos2x 2sin x.

Последнее уравнение равносильно системе

				2	x
5cosx cos2x 4sin

sin x 0
Решим уравнение системы
5cosx (2cos2		x 1) 4(1 cos2 x);
2cos2 x 5cosx 3 0.
Отсюда cosx	1	или cosx 3(нет кор-

2			1
ней). Из уравнения cosx					получаем

		2

sin x

http://vk.com/ege100ballov

x	2 n, n Z или	x	2 n,

3		3
n Z .

Проверим для полученных значений x выполнение условие sin x 0:

										3				3
	sin		2 n		sin							,			0;
	sin		2 n		sin					2		,		2	0;
		3					3			2				2

											3					3
sin		2 n		sin									,				0.
sin		2 n		sin						2			,		2		0.
	3					3				2					2
					Ответ:					2 n, n Z.
					Ответ:					2 n, n Z.
									3
Пример 16. Решить уравнение:

				1		1		ctg x.
				1				ctg x.
						sin x

Решение. Данное уравнение равносильно смешанной системе

									ctgx 0,
									1
			1						1			ctg2		x.
			1									ctg2		x.
								sin x
								sin x
Вначале решим уравнение:
			1						1	ctg2 x;
			1				sin x			ctg2 x;
							sin x
		1				1					1			1;
		1									sin2 x			1;
					sin x						sin2 x
		1							1					1
1												1			1	;
1												1			1	;
	sin x					sin x							sin x
			1								1
1									2					0 .
1									2					0 .
				sin x									sin x

В области определения, которое задается условием sin x 0, последнее уравнение распадается на два, равносильных ему в совокупности уравнения:

1) 1	1	0; sinx 1;

sin x

x 2 n, n Z.

2) 2 0; sin x 1 ; 2

x 1 n n, n Z.

Отберем значения x, удовлетворяющие условию ctgx 0.

Для

корней

первой

серии

ctg

2 n

0, следовательно,

усло-

вие ctgx 0

выполнено

для

всех

2 n, n Z.

Для корней второй серии

ctg

( 1)

ctg ( 1)

3,еслиn четно,

3,еслиnнечетно.

Таким образом, условие ctgx 0 выполнено только для четных значений

n (n 2m, m Z), т.е. для x 2 m.

Ответ: 2 n, 2 n, n Z.

2 6

Пример 17. Решите уравнение:

cos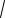2 x2 3 . 2

Решение. Рассматривая данное уравнение как простейшее тригонометрическое уравнение, получим

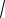2 x2 2 n, n Z. 6

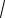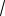Так как 2 x2 2, то 0 2 x2 2.

Из всех чисел вида 2 n, n Z от- 6

резку [0;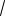2] принадлежит только число

. Поэтому последнее уравнение равно- 6

сильно уравнению

2 x2 . 6

Возведя обе части уравнения в квадрат, получим

x2	2	2	, откуда x	2		2	.
x2	2		, откуда x	2			.
	36				36
			Ответ: 2					2
									.
									.
						36

http://vk.com/ege100ballov

7. Уравнения, содержащие показательные выражения

Пример 18. Решить уравнение:


3cosx cos x
3cosx cos x
			27 .


		3cosx
	3	3cosx

Решение. Преобразуем данное уравнение


cos2 x	3		cos x			3

3	2			32			;
		cosx			3
cos2 x	3						0.

2				2
Обозначив cos		x t ,		где 1 t 1,

получим для неизвестной t квадратное

уравнение 2t2
уравнение 2t2				3t 3 0, которое имеет
корни t		3	и t				(не удовлетво-
		3			2	3
						3
1	2
	2

ряет условию 1 t 1).

Выполнив обратную замену, из урав-

нения cosx 3 получаем

x 5 2 n, n Z. 6

Ответ: 5 2 n, n Z. 6

Пример 19. Решите уравнение:

Решение. Так как 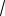x 0, то 3 x 1. Левая часть уравнения ограничена, так

		13x
как 1 cos	22		1. Поэтому

		4

данное уравнение равносильно системе

				13x
cos			22		1
cos			22		1
				4

	x	1
3		1

cos22 1(верно)

x 0

Ответ: 0.

8. Уравнения, содержащие логарифмические выражения

Пример 20. Решите уравнение:

log2 (sin x) log2 ( cosx).

Решение. Данное уравнение равносильно системе

sin x cosx,

sin x 0.

Из уравнения системы получаем

tgx 1, x n, n Z. Неравенст- 4

ву sin x 0 удовлетворяют числа

x 3 2 n, n Z. 4

Ответ: x 3 2 n, n Z. 4

Пример 21. Решите уравнение: log2 ( sin x) log2 (cosx) 2

Решение. Данное уравнение равносильно смешанной системе:

sin x 0,

cosx 0,

log2 ( sin xcosx) 2

sin x 0,

cosx 0,

sin xcosx 0,25.

Решим вначале уравнение этой системы:

sin xcosx 0,25					sin2x 0,5

2x			2 n,			n Z,
2x	6		2 n,			n Z,
	6
	5
	5
2x				2 k, k Z,
2x	6			2 k, k Z,
	6

x					n,	n Z,
x					n,	n Z,
	12
		5
		5
x					k,	k Z.
x					k,	k Z.
	12
Условиям sin x 0 и						cosx 0	удов-

летворяет совокупность значений x, принадлежащих четвертой координатной четверти. Тогда решения исходного уравнения можно записать следующим образом:

http://vk.com/ege100ballov

12 2 n, n Z,

x 5 2 k, k Z.12x

Ответ: 2 n, n Z ; 5 2 k , 12 12

k Z.

9. Уравнения, содержащие модули Пример 22. Решить уравнение:

| cosx| 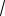3sin x.

Решение. Из данного уравнения получаем равносильную систему

cosx
cosx	3sin x				3
				tgx	3
				tgx	3 n Z
cosx		3sin x			3 n Z


sin x 0				sin x 0

		x		n
		x	6	n
			6	n Z .

sin x 0

Так как функции tgx и sin x имеют общий наименьший положительный период 2 , то отбор корней проведем на тригонометрическом круге (сделайте рисунок).

Ответ: 2 k;5 2 n;k,n Z. 6 6

Пример 23. Решите уравнение:

| cosx| cosx 2sin x.

Решение. Рассмотрим две области на числовой прямой, на которых cosx 0 и cosx 0.

1) Пусть cosx 0, тогда данное уравнение принимает вид:

cosx cosx 2sin x sin x 0

x n, n Z.

Условию cosx 0 удовлетворяют только значения x 2πn, n Z.

2) Для условия cosx 0 исходное уравнение перепишем так:

cosx cosx 2sin x sin x cosx 0

tgx 1 x k, k Z. 4

Условию cosx 0 удовлетворяют

только значения x 3 2 k, k Z. 4

Ответ: 2πn, n Z; 3 2 k, k Z. 4

Пример 24. Решите уравнение:

7|cosx| 4cosx 3|sin x| 2sin x.

Решение. Рассмотрим значения синуса и косинуса по четвертям координатной окружности.

Первая четверть:

3cosx 5sin x		tgx	3
3cosx 5sin x		tgx
	3	5
x arctg	3	2 k, k Z.
x arctg		2 k, k Z.
5
Вторая четверть:				11
11cosx 5sin x		tgx		11
11cosx 5sin x		tgx
		5

x arctg11 2 l, l Z. 5

Третья четверть:

11cosx sin x tgx 11

x arctg11 2 m, m Z.

Четвертая четверть:

3cosx sin x tgx 3

x arctg3 2 n, n Z.

Ответ: arctg	3	2 k,	arctg	11	2 l,

5			5
arctg11 2 m,			arctg3 2 n, где
			k,l,m, n Z.

Пример 25. Решите уравнение:

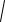(3sin 0,25x 4)2

sin2 0,25x 6sin 0,25x 9 1 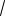2 .

Решение. Имеем

| 4 3sin0,25x| |3 sin0,25x| 1 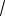2 .

Так как при всех x R

4 3sin0,25x 0,		3 sin0,25x 0,
то получаем
		sin0,25x		;
1 2sin0,25x 1			2
	2;

x ( 1)n 4 n, n Z.

Ответ: ( 1)n 4 n, n Z.

http://vk.com/ege100ballov

10.Уравнения, содержащие обратные тригонометрические функции

Пример 26. Решите уравнение:

arccos(x2 3) arccos(x 3).

Решение. Уравнение равносильно системе

	2	3 x 3,		2	x 6 0,
x			x
1 x 3 1			4 x 2

x 2
	x 2.
x 3	x 2.

4 x 2
	Ответ: 2.

Пример 27. Решите уравнение:

arccosx arcsin 2x .

Решение. Область допустимых значений уравнения определяется условиями x 1, 2x 1, т.е. x 0,5. Более того,

поскольку значения арккосинуса ограничены отрезком 0, , а арксинуса – отрез-


ком		;		, то равенство левой и пра-
	2		2

вой частей уравнения возможно только в случае, если их значения лежат на отрез-


ке	0;		, т.е. с учетом области допусти-

		2
мых		значений переменной х имеем

0 x 0,5.

Таким образом, решение уравнения следует искать на множестве 0 x 0,5. Так как функция y cost убывает на от-

нение arccosx arcsin 2x равносильно

уравнению

cos arccosx cos arcsin 2x ,

которое, в свою очередь, на 0;0,5

рав-

носильно

уравнениям:

1 4x2 ,

x2 1 4x2 ,

5x2 1,

(при

0 x 0,5).

Ответ:

Пример 28. Решите уравнение:

arccos3x 4 x 6 . 1 2x

Решение. В соответствии с определением арккосинуса запишем ограничения, которым должна удовлетворять переменная x. Область допустимых значений уравнения определяется условиями

1 3x 4 1, а поскольку значения

1 2x

арккосинуса ограничены отрезком 0, , то для выполнения равенства необходимо выполнение условия 0 x 6 . Получаем систему неравенств

					3x 4		1,
	3x 4						1,
	3x 4
1		1,			1 2x
1	1 2x	1,			1 2x
	1 2x				3x 4
							1,
							1,
0 x 6					1 2x
					0 x 6 1
	x 5		0,

	1 2x
	1 2x
						x 5.
	5x 3					x 5.
				0,
		1 2x		0,
		1 2x
	6 x 5

Подставляя полученное единственное значение x 5 в исходное уравнение, получим

arccos3 ( 5) 4 ( 5) 6 , 1 2 ( 5)

arccos 11 или arccos( 1) верно. 11

Следовательно, данное уравнение имеет единственное решение x 5.

Ответ: 5.

11. Комбинированные уравнения

Пример 29. Решите уравнение:

(2cosx 1)log13 (3tg2 x) 0. log31 (2sinx)

Решение. Из данного уравнения получа-

ем два		уравнения cosx 0,5 или
tgx	3	при условии
tgx		при условии

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.08.201974.73 Кб2Madatov.docx
#
14.04.2015149.5 Кб42magazin-odezhdy.doc
#
21.03.20165.26 Mб56Marc G. Jeschke - Burn Care and Treatment A Practical Guide - 2013.pdf
#
15.04.2015231.66 Кб24matanok.pdf
#
14.11.20192.32 Mб43matematika_predel_i_proizvodnaya.doc
#
15.04.20151.1 Mб24matematika_С1.pdf
#
10.07.2019942.59 Кб15MATYeMATIChYeSKAYa_STATISTIKA_2_vvedenie.doc
#
14.04.2015954.37 Кб66Menedzhment.doc
#
11.11.20194.91 Mб206METOD-all.doc
#
27.08.2019138.75 Кб19Metodicheskme_guidance_on_writing_term_papers.doc
#
15.04.20151.27 Mб24metodichka2-vsya-isp-1-format70kh108-16.pdf