15.2. Некоторые теоремы о дифференцируемых функциях

Теорема 15.2 (Ролля).

Е сли функция f(x) непрерывна на отрезке [a, b], дифференцируема в интервале (a, b) и на концах отрезка принимает одинаковые значения f(a)=f(b), то найдется такая точка , в которой производная обращается в нуль: .

Геометрически теорема Ролля означает. что на графике функции y=f(x) найдется точка, в которой касательная к графику параллельна оси Ох.

Так, для функции на рисунке таких точек две.

Теорема 15.3. (Лагранжа).

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b), то найдется такая точка , что выполняется равенство

.

Перепишем формулу Лагранжа в виде . Отношение есть угловой коэффициент секущей графика функции, проходящей через концевые точки.

Таким образом, геометрически теорема Лагранжа означает, что на графике функции найдется точка С, в которой касательная параллельна секущей АВ.

Следствие. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке.

Обобщением теоремы Лагранжа является

Теорема 15. 4. (Коши).

Если функции f(x) и g(x) непрерывны на отрезке [a,b] и дифференцируемы в интервале (a, b), причем в этом интервале, то найдется такая точка , что выполняется равенство

.

15.3. Исследование поведения функций и построение графиков

• Возрастание и убывание функций

Теорема 15.5. 1) Если функция , имеющая производную на отрезке , возрастает (убывает) на этом отрезке, то ее производная на отрезке неотрицательна (неположительна), т.е. ( ).

2) Если функция непрерывна на отрезке и дифференцируема в промежутке , причем ь ( ) для , то эта функция возрастает (убывает) на .

Геометрический смысл этой теоремы в том, что касательные к графику дифференцируемой возрастающей функции образуют острые углы, а убывающей функции – тупые углы с положительным направление оси .

• Максимум и минимум функций.

• Функция в точке имеет максимум, если значение функции в точке больше, чем ее значения во всех точках некоторой окрестности точки .Иначе говоря, функция имеет максимум при , если , при любых .

• Функция имеет минимум при , если , при любых .

• Максимумы и минимумы функции называются экстремумами.

Теорема 15.6 (необходимое условие существования экстремума). Если дифференцируемая функция имеет в точке экстремум, то ее производная обращается в нуль в этой точке, т.е. .

• Точки, в которых производная функции обращается в нуль или не существует, называются критическими.

Теорема 15.7 (достаточное условие существования экстремума). Пусть функция непрерывна в некотором интервале, содержащем критическую точку , и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при функция имеет максимум. Если же при переходе через точку функция меняет знак с минуса на плюс, то функция имеет в этой точке минимум.

• Выпуклость и вогнутость кривой. Точки перегиба.

• Говорят, что кривая обращена выпуклостью вверх на интервале , если все точки кривой лежат ниже любой ее касательной на этом интервале. Говорят, что кривая обращена выпуклостью вниз на интервале , если все точки кривой лежат выше любой ее касательной на этом интервале. Кривую, обращенную выпуклостью вверх будем называть выпуклой, а обращенную выпуклостью вниз – вогнутой.

Теорема 15.8. 1) Если во всех точках интервала , то кривая на этом интервале выпукла.

2) Если во всех точках интервала , то кривая на этом интервале вогнута.

• Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой.

В точке перегиба касательная, если она существует, пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны над нею.

Теорема 15.9. Пусть кривая определяется уравнением . Если или не существует и при переходе через значение вторая производная меняет знак, то точка с абсциссой является точкой перегиба.

• Асимптоты

• Прямая l называется асимптотой кривой, если расстояние  от точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.

Различают два вида асимптот: вертикальные и наклонные.

• Прямая 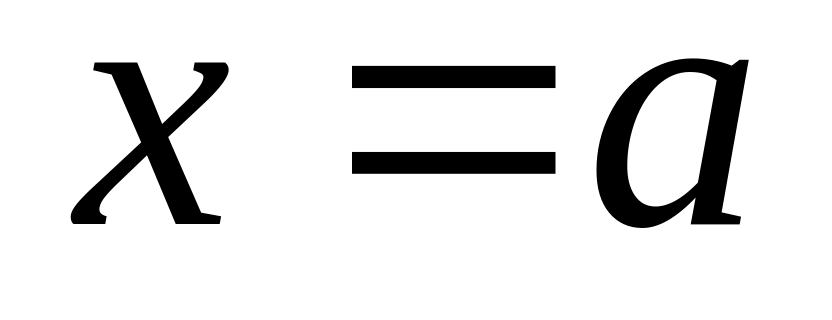является вертикальной асимптотой графика функции , если .

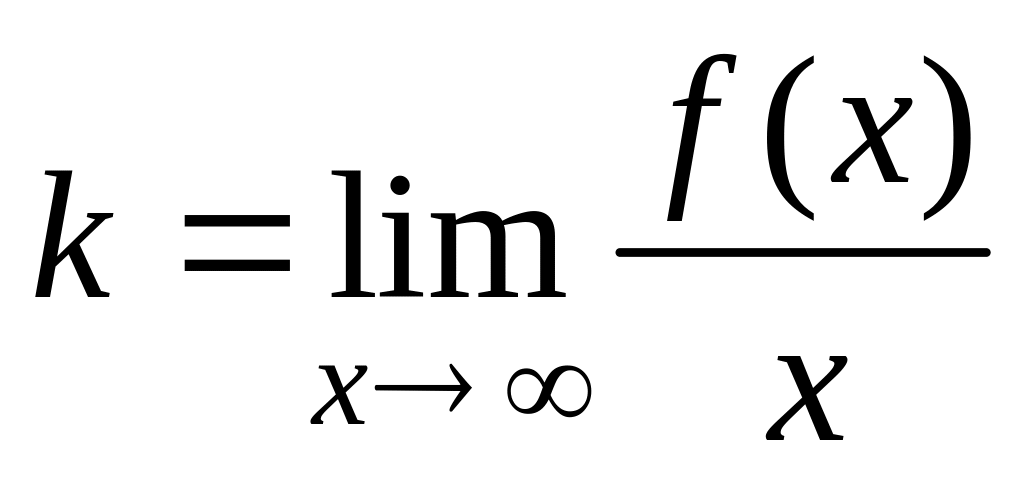• Уравнение наклонной асимптоты , где , а .

• В частности, если , то – уравнение горизонтальной асимптоты.

Замечание. Асимптоты графика функции при и могут быть разными, поэтому при вычислении пределов следует отдельно рассматривать случаи и .