§11. Бесконечно малые функции

11.1. Определение и основные теоремы

• Функция называется бесконечно малой функцией (БМФ) при , если .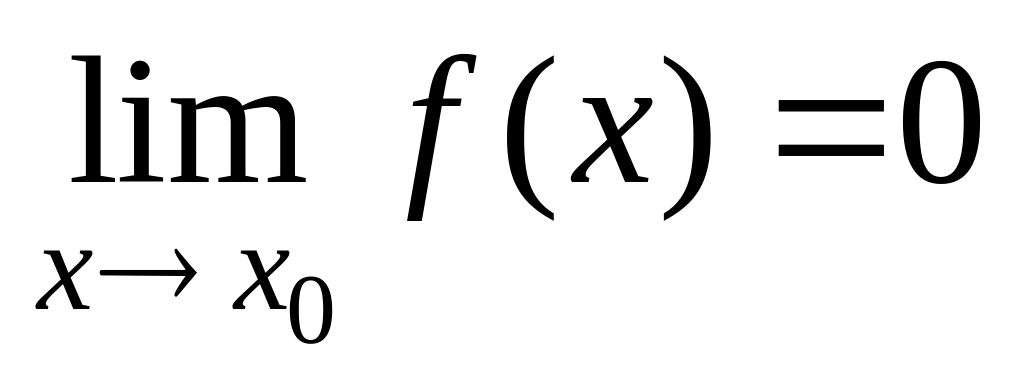

Например, при является функцией бесконечно малой, а функция является бесконечно малой функцией при .

Теорема 11.1. Алгебраическая сумма бесконечно малых функций есть бесконечно малая функция.

Теорема 11.2. Произведение бесконечно малой функции на ограниченную функцию есть БМФ.

Следствие 1. Произведение конечного числа БМФ есть БМФ.

Следствие 2. Произведение БМФ на число есть БМФ.

Теорема 11.3. Частное от деления БМФ на функцию, имеющую предел, отличный от нуля – есть БМФ.

Теорема 11 4. Если – БМФ, то – ББФ. Обратно, если – ББФ, то – БМФ.

Теорема 11.5. функцию можно представить как сумму числа А и бесконечно малой функции .

Доказательство: Пусть . Следовательно, по определению, такое, что для всех х из -окрестности точки х₀ выполняется неравенство , то есть , а это значит, что , то есть функция есть БМФ. Обозначив , получаем , что и требовалось доказать.

Обратно, пусть , где - БМФ. То есть такое, что для всех х из -окрестности точки х₀ выполняется неравенство , то есть , а это означает по определению предела функции в точке, что .

11.2. Основные теоремы о пределах

Теорема 11.6. Предел суммы двух функций равен сумме пределов.

Доказательство. Пусть  по теореме.5 , где - БМФ. Аналогично, если , то , где - БМФ.

Тогда

Поскольку сумма двух бесконечно малых функций есть функция бесконечно малая, следовательно – бесконечно малая функция. Таким образом, по теореме 5, получим:

Следствие. Если предел функции существует, то он

единственный.

Теорема 11.7. Предел произведения двух функций равен произведению пределов, т.е. .

Теорема 11.8. , если .

Теорема 11 9. (Теорема о пределе промежуточной функции.)

Е сли функция такова, что и , то .

Теорема 11.10. Если функция монотонна и ограничена при ( ), то существует

( ).

11.3. Техника вычисления пределов. Примеры

Для вычисления пределов вида , где и многочлены степеней и , необходимо вынести за скобку в числителе и в знаменателе .

Пример 1.

.

Для вычисления пределов вида необходимо привести их к пределам вида .

Пример 2.

. (В данной задаче для преобразования предела к виду использовалось приведение к общему знаменателю).

Пример 3.

= . (В данной задаче для преобразования предела к виду умножили и разделили на сопряженное).

Для вычисления пределов вида необходимо выяснить, определена ли функция при . Если принадлежит области определения функции , то .

Пример 4. .

Если и , то .

Пример 5. .

При и , т.е. если , необходимо (в случае и ) разделить числитель и знаменатель на .

Пример 6.

.

Пример 7.

=

.

11.4. Первый замечательный предел

Рассмотрим функцию . Она не определена при , так как числитель и знаменатель дроби обращаются в нуль. Однако можно заметить, что если , то значения функций и приблизительно одинаковые. Это можно увидеть на представленном ниже рисунке и сравнить значения в таблице.

Значения аргумента
	0,785	0,71
	0,523	0,5
	0,17	0,17
	0,017	0,017

Ч ем ближе , тем больше и схожи в значениях. Таким образом, можно заключить, что при функция . Итак, докажем формулу . Для этого рассмотрим единичную окружность. Пусть .

, , .

Так как , то .

Разделим данное неравенство на . Знак неравенства при этом не изменится, поскольку лежит в I четверти. Получим:

.

Следовательно, . Воспользуемся теоремой о пределе промежуточной функции. Поскольку при функция и , тогда при .

Итак,

Ниже представлен график функции .