- •Тема III – основы математического анализа
- •§8. Множества и операции над ними
- •8.1. Основные понятия
- •8.2. Числовые множества
- •9. Функция
- •9.1. Понятия функции и ее графика
- •9.2. Способы задания функций
- •9.3. Некоторые свойства функций
- •9.4. Обратная функция
- •9.5. Основные элементарные функции
- •9.5. Сложная функция и элементарные функции
- •§10. Предел функции
- •10.1. Предел функции в точке
- •10.2. Односторонние пределы
- •10.3. Предел функции на бесконечности
- •10.4. Бесконечно большие функции
- •§11. Бесконечно малые функции
- •11.1. Определение и основные теоремы
- •11.2. Основные теоремы о пределах
- •11.3. Техника вычисления пределов. Примеры
- •11.4. Первый замечательный предел
- •11.5. Эквивалентные функции
- •11.6. Второй замечательный предел
- •11.7. Техника вычисления пределов вида .
- •§12. Непрерывность функции
- •12.1. Непрерывность функции в точке и в области
- •12.2. Основные теоремы о непрерывных функциях
- •12.3. Классификация точек разрыва
- •§13. Производная функции
- •13.1. Приращение аргумента и приращение функции
- •13.2. Определение производной функции в точке
- •13.3. Геометрический смысл производной
- •13.4. Физический смысл производной
- •13.5. Дифференцируемость функций
- •13.6. Производная постоянной, суммы, произведения и частного двух функций
- •13.7. Производная сложной и обратной функции
- •13.8. Производные основных элементарных функций
- •13.9. Производная функции, заданной неявно
- •13.10. Логарифмическая производная
- •13.11. Производная функции, заданной параметрически
- •13.13. Примеры вычисления производных
- •13.14. Производные высших порядков
- •§14. Дифференциал функции
- •14.1. Понятие дифференциала функции
- •14.2. Основные теоремы о дифференциалах
- •14.3. Применение дифференциала к приближенным вычислениям
- •§15. Исследование функций при помощи производных
- •15.1. Правило Лопиталя
- •15.2. Некоторые теоремы о дифференцируемых функциях
- •15.3. Исследование поведения функций и построение графиков
- •Общее исследование функции и построение ее графика рекомендуется выполнять по следующей схеме:
9.3. Некоторые свойства функций
Функция
 ,
определяемая на множестве D
является четной,
если
,
определяемая на множестве D
является четной,
если
 выполняются условия
выполняются условия
 и
и
 ;
нечетной,
если
выполняются условия
и
;
нечетной,
если
выполняются условия
и
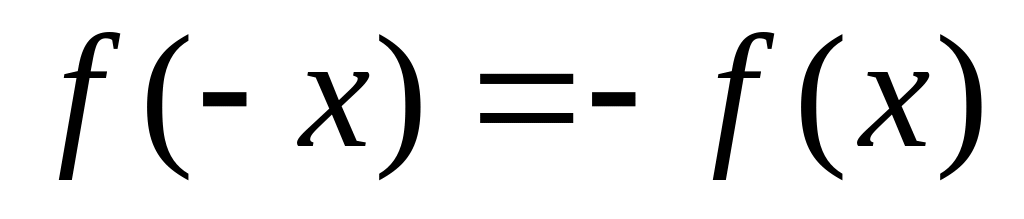 .
График четной функции симметричен
относительно оси ординат, а график
нечетной функции симметричен относительно
начала координат.
.
График четной функции симметричен
относительно оси ординат, а график
нечетной функции симметричен относительно
начала координат.Функция определена на множестве D и пусть
 .
Если для любых значений
.
Если для любых значений
 :
:
 ,
то функция называется возрастающей
на множестве
,
то функция называется возрастающей
на множестве
 ;
;
 ,
то функция называется убывающей
на множестве
;
,
то функция называется убывающей
на множестве
;
 ,
то функция называется неубывающей
на множестве
;
,
то функция называется неубывающей
на множестве
;
 ,
то функция называется невозрастающей
на множестве
.
Возрастающие, убывающие, неубывающие,
невозрастающие функции на
называются монотонными
на этом множестве, а возрастающие и
убывающие – строго
монотонными.
Интервалы, в которых функция монотонна
называются интервалами
монотонности.
,
то функция называется невозрастающей
на множестве
.
Возрастающие, убывающие, неубывающие,
невозрастающие функции на
называются монотонными
на этом множестве, а возрастающие и
убывающие – строго
монотонными.
Интервалы, в которых функция монотонна
называются интервалами
монотонности.Функцию , определенную на множестве D, называют ограниченной на этом множестве, если существует такое число
 ,
что для всех
,
что для всех
 выполняется неравенство
выполняется неравенство
 .
График ограниченной функции лежит
между прямыми
.
График ограниченной функции лежит
между прямыми
 и
и
 .
.Функцию , определенную на множестве D, называют периодической на этом множестве, если существует такое число
 ,
что при каждом
значение
,
что при каждом
значение
 и
и
 .
Число
.
Число
 называется периодом функции.
называется периодом функции.
9.4. Обратная функция
Пусть
задана функция
с областью определения D
и множеством значений E.
Если каждому значению
![]() соответствует единственное значение
,
то определена функция
соответствует единственное значение
,
то определена функция
![]() с областью определения E
и множеством значений D.
Такая функция
называется обратной
к функции
.
с областью определения E
и множеством значений D.
Такая функция
называется обратной
к функции
.
Из
определения обратной функции вытекает,
что функция
имеет обратную тогда и только тогда,
когда каждому
соответствует единственное
и наоборот, то есть когда функция
задает взаимнооднозначное соответствие
между множествами
![]() и
и
![]() .
Тогда всякая строго монотонная функция
имеет обратную, при этом если функция
возрастает (убывает), то обратная функция
также возрастает (убывает).
.
Тогда всякая строго монотонная функция
имеет обратную, при этом если функция
возрастает (убывает), то обратная функция
также возрастает (убывает).
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
9.5. Основные элементарные функции
Среди огромного числа функций в ходе развития математики была выделена небольшая совокупность сравнительно простых функций, особенно часто встречающихся в самых разнообразных приложениях математического анализа и поэтому подвергнутых наиболее подробному исследованию. Их называют основными элементарными функциями. К ним относят функции степенную, показательную и логарифмическую, тригонометрические и обратные тригонометрические функции.
Степенная функция – это функция вида
 ,
где
,
где
 .
.
Пусть
 .
Тогда данная функция определена для
всех
.
Тогда данная функция определена для
всех
 .
.
Рис. 1


Рис. 2
 Рис.
3
Рис.
3
Пусть n – целое отрицательное число. В этом случае функция определена при всех
 .
.
Рис. 4


Рис. 5

Пусть n – произвольное действительное число, тогда степенная функция будет определена при x > 0.
Рис. 6
|
Рис. 7 |
На рис. 7 представлена совокупность степенных функций при различных положительных значениях n.
Показательная функция – это функция вида
 ,
где
,
где
 и
и
 .
Она определена при всех x.
.
Она определена при всех x.
Рис. 8
|
|
На рисунке 10 представлена совокупность показательных функции при различных значениях основания .

Рис. 10
Логарифмическая функция – функция вида
 ,
,
 .
Она определена при
.
Она определена при
 .
.
Напомним,
что, по определению логарифма,
![]() ,
так что логарифмическая функция является
обратной для показательной функции
.
,
так что логарифмическая функция является
обратной для показательной функции
.
Заметим,
что одним из наиболее часто встречающихся
и удобных является логарифм по основанию
е
– натуральный логарифм
![]() ;
кроме того, всегда можно выразить
;
кроме того, всегда можно выразить
![]() .
.
Рис. 11
|
Рис. 12
|
Тригонометрические функции.
К
тригонометрическим относят следующие
функции:
,
![]() ,
,
![]() .
.
![]() .
Их графики представлены на рисунках
13-16.
.
Их графики представлены на рисунках
13-16.

Рис.13

Рис.14

Рис. 15

Рис. 16
![]()
Обратные тригонометрические функции.
К
обратным тригонометрическим функциям
относят:
![]() - функция, обратная для функции sinx
на интервале ее монотонности:
- функция, обратная для функции sinx
на интервале ее монотонности:
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Графики первых трех функций представлены ниже.
Рис. 17
|
Рис. 18
|

Рис. 19




 Рис.
9
Рис.
9