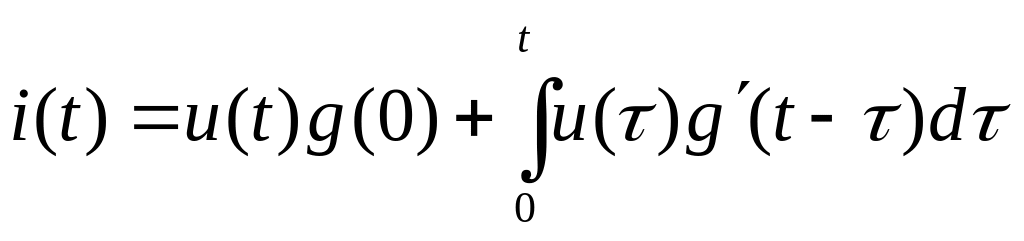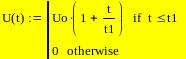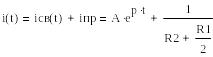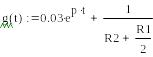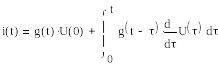- •Постоянный ток
- •§ 1.1. Законы Кирхгофа.
- •§ 1.2. Примеры использования законов Кирхгофа
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12. Метод наложения (метод суперпозиции).
- •§2 Переменный ток
- •§2.1. Синусоидальные ток и напряжение. Символический метод
- •Немного о комплексных числах
- •Показания приборов
- •Векторные диаграммы – фазовые соотношения между величинами
- •Мощность в цепи переменного тока
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •Метод симметричных составляющих
- •Переходные процессы Переходные процессы в простейших цепях
- •Кассический метод расчета переходного процесса Первый и второй законы коммутации, Понятия о зависимых и независимых начальные условиях
- •Метод расчета переходных процессов в цепи переменный тока
- •Переходные процессы в цепи второго порядка
- •Операторный метод расчёта переходных процессов
- •Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Формулы для определения напряжения и тока в любой точке линии через комплексы тока и напряжения в начале линии
- •Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •Линии без потерь
- •Коэффициент отражения
- •Действующие значения напряжения и тока вдоль линии без потерь
- •Стоячие волны
- •Входное сопротивление линии без потерь при холостом ходе
- •Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
Метод расчета переходных процессов в цепи переменный тока
Для расчета переходный процессов в цепи переменного тока используют символический метод
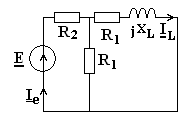
Пример: Определить ток источника
напряжения если
![]()
Р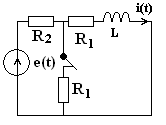 ешение:
Находим индуктивное сопротивление
и комплекс напряжения
ешение:
Находим индуктивное сопротивление
и комплекс напряжения
![]() .
.
Ищем решение в виде
![]()
1. Определяем принужденную составляющую в цепи после коммутации, используя символический метод
![]()
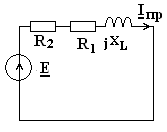
Определяем мгновенное значение принужденного тока
![]()
2. Определяем корень характеристического уравнения
![]()
3. Определяем независимые независимые
начальные условия
![]() используя
символический метод.
используя
символический метод.
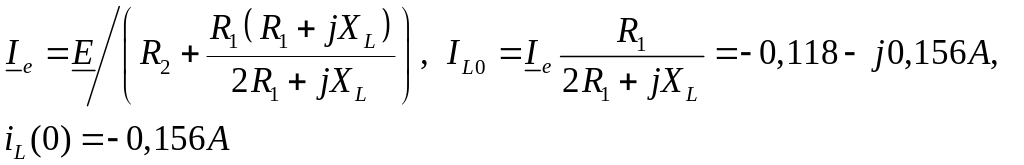
О
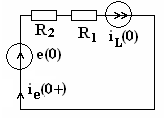 пределяем
зависимые начальные условия в схеме
после коммутации, заменяя индуктивность
источником тока равным
.
пределяем
зависимые начальные условия в схеме
после коммутации, заменяя индуктивность
источником тока равным
.
![]()
Определяем константу интегрирования
![]()
Записываем решение и строим график.

![]()
Строим зависимость в пределах одного периода
|
Переходные процессы в цепи второго порядка
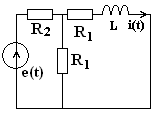
Рассмотрим цепь второго порядка представленную на рисунке с параметрами:
![]()
Записываем уравнения по второму закону Кирхгофа, в результате получаем систему дифференциальных уравнений:
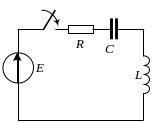
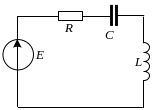
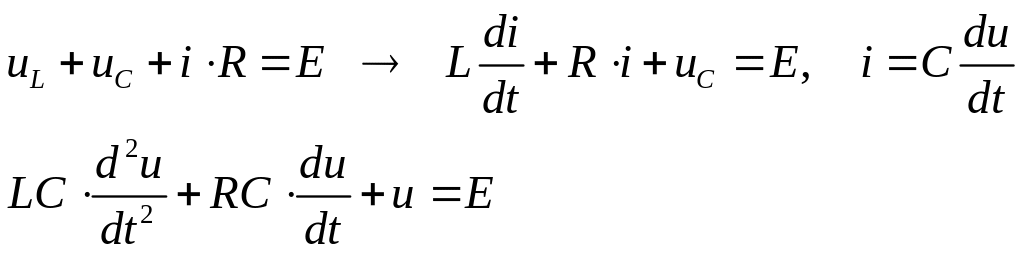 (1)
(1)
Решение данного уравнения будем искать в виде суммы двух составляющих:
![]() .
(2)
.
(2)
Первое слагаемое это
![]() свободная
составляющая. Она зависит только от
параметров схемы, а также от начальных
и конечных запасов энергии. Эта
составляющая решения не зависит от
формы воздействующего напряжения.
свободная
составляющая. Она зависит только от
параметров схемы, а также от начальных
и конечных запасов энергии. Эта
составляющая решения не зависит от
формы воздействующего напряжения.
Второе слагаемое это![]() принуждённая составляющая. Она зависит
от внешнего воздействия и имеет форму
этого воздействия. Очевидно, что в нашем
случае она определяется как
принуждённая составляющая. Она зависит
от внешнего воздействия и имеет форму
этого воздействия. Очевидно, что в нашем
случае она определяется как
![]() .
.
Постоянные интегрирования определяются из начальных условий, отражающих невозможность мгновенного изменения начальных запасов энергии в конденсаторе и в катушке.
Для определения констант интегрирования
используем независимые начальные
условия
![]() .
.
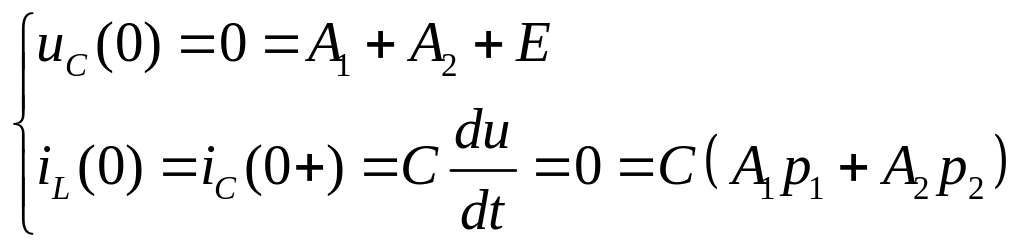 (3)
(3)
Откуда следует, что
![]() (4)
(4)
Теперь можно записать окончательное решение
![]()
Определим корни характеристического
уравнения входящие в решение
![]()
![]() через входное сопротивление схемы.
через входное сопротивление схемы.
![]() (5)
(5)
В результате решения уравнения получаются корни:
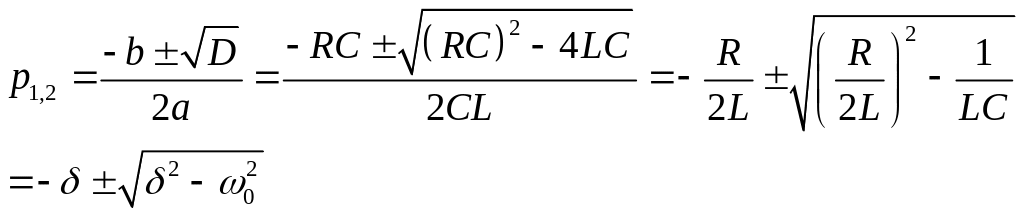 (6)
(6)
Где
![]() – показатель затухания контура,
– показатель затухания контура,
![]() – угловая частота незатухающих колебаний,
– угловая частота незатухающих колебаний,
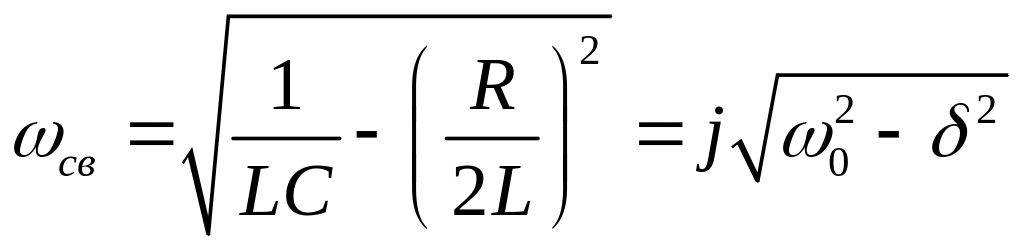 – частота свободных колебаний,
– частота свободных колебаний,
Корни уравнения определяются параметрами цепи и могут принимать следующие возможные значения.
Дискриминант равен нулю. Кони вещественные, отрицательные и кратные. Критический режим
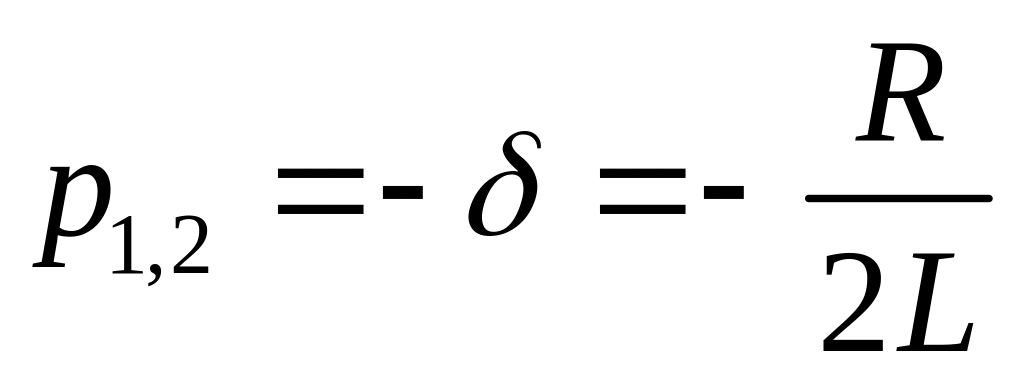
![]() .
.
Дискриминант положительный. Корни вещественные отрицательные и неравные. Апериодический режим
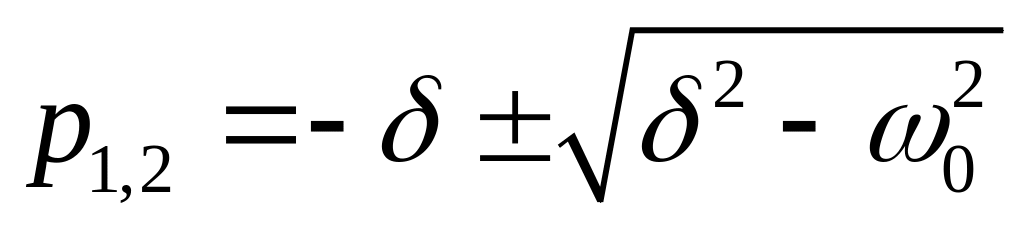
![]() .
.
Дискриминант отрицательный. Корни комплексно-сопряжённые, с отрицательной вещественной частью. Колебательный режим

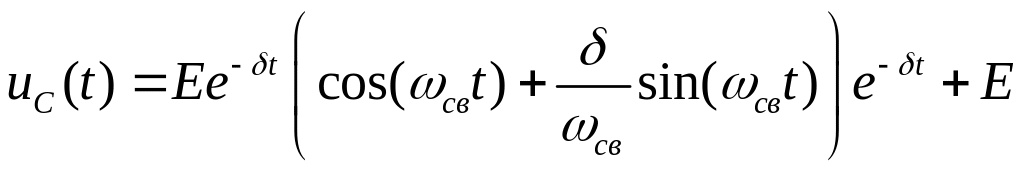
С оответствующее
расположение корней указанно на
комплексной плоскости.
оответствующее
расположение корней указанно на
комплексной плоскости.
Операторный метод расчёта переходных процессов
Операторный метод (преобразование Лапласа) расчета переходных процессов используется для того, чтобы обыкновенные дифференциальные уравнения с постоянными коэффициентами (в пространстве оригиналов) преобразовать в алгебраические (в пространстве изображений). Очевидно, что алгебраические уравнения решаются проще. После решения алгебраического уравнения над полученной функцией (изображением) производится обратное преобразование Лапласа, получается оригинал. Полученный оригинал – это функция, которая и будет решением дифференциального уравнения.
Любой функции можно сопоставить её преобразование Лапласа
![]() (1)
(1)
здесь
![]() – изображение,
– изображение,
![]() – оригинал. Выражение (1) записывают ещё
и в операторной форме
– оригинал. Выражение (1) записывают ещё
и в операторной форме![]() .
.
Приведём изображение нескольких часто встречающихся функций.
Определим изображение константы –
![]() :
:
![]()
Найдем изображение экспоненциальной
функции –
![]() :
:
![]()
Изображение экспоненциальной функции
поможет нам найти изображения
синусоидальной косинусной функций–
![]() .
Для этого запишем эти функции через
формулу Эйлера. Далее осуществляем
следующую цепочку преобразований:
.
Для этого запишем эти функции через
формулу Эйлера. Далее осуществляем
следующую цепочку преобразований:
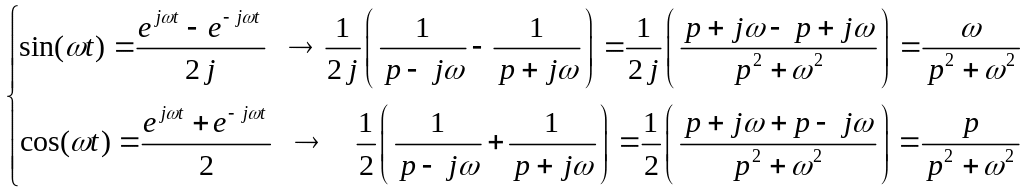
Определим изображение производной
![]() функции
,
имеющей изображение
функции
,
имеющей изображение
![]()
И, наконец, определим изображение
интегрального выражения![]()
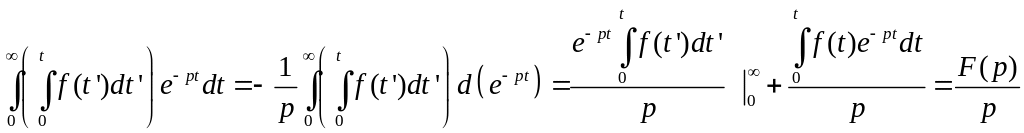
таблица преобразований лапласса
-
-оригинал
-изображение
1
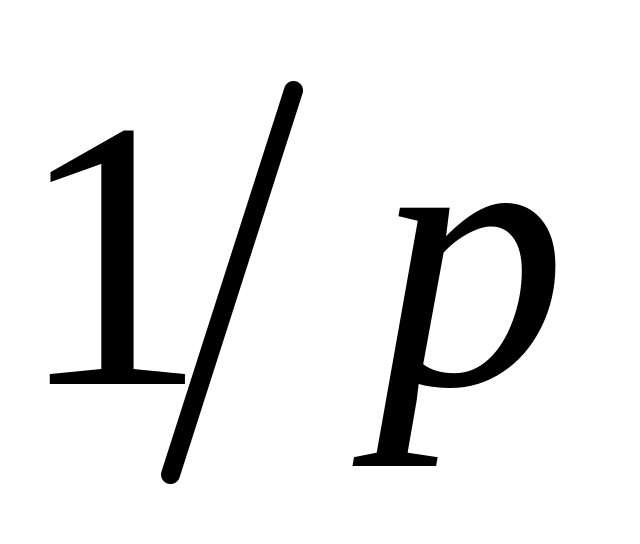

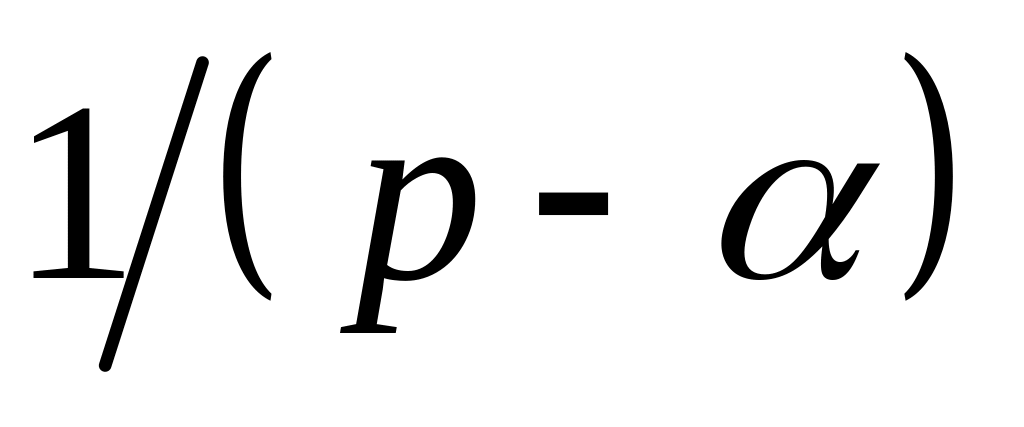
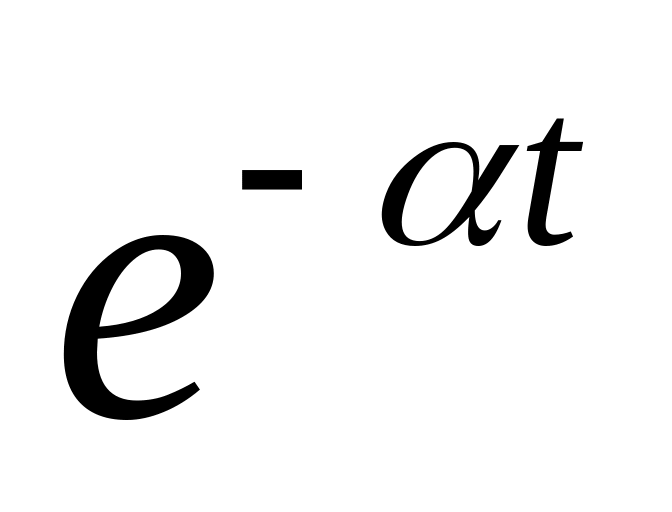
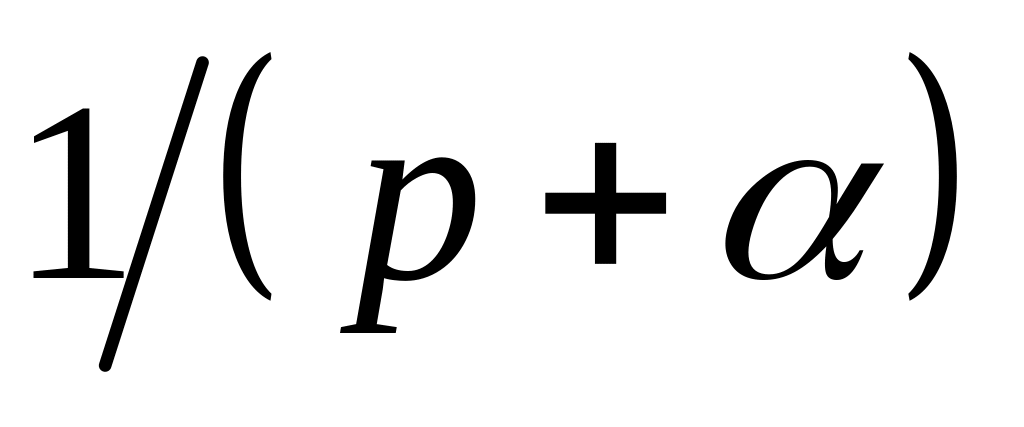
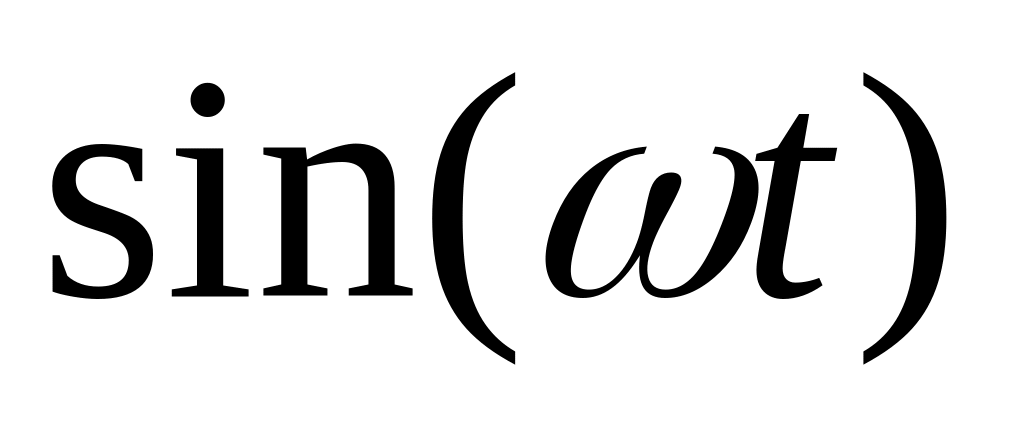
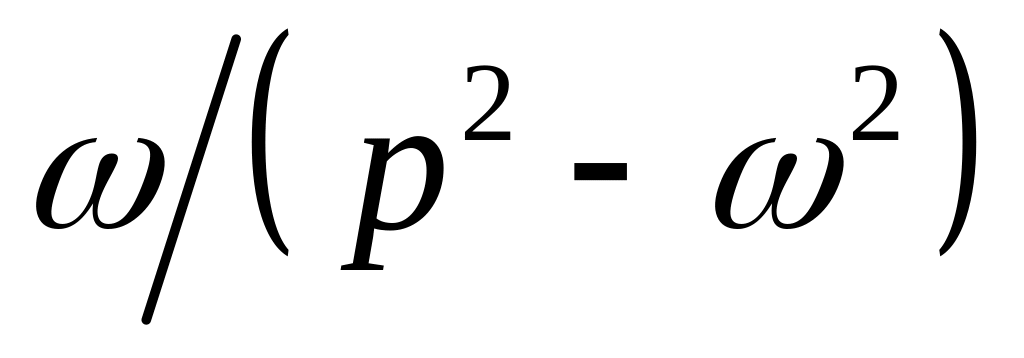
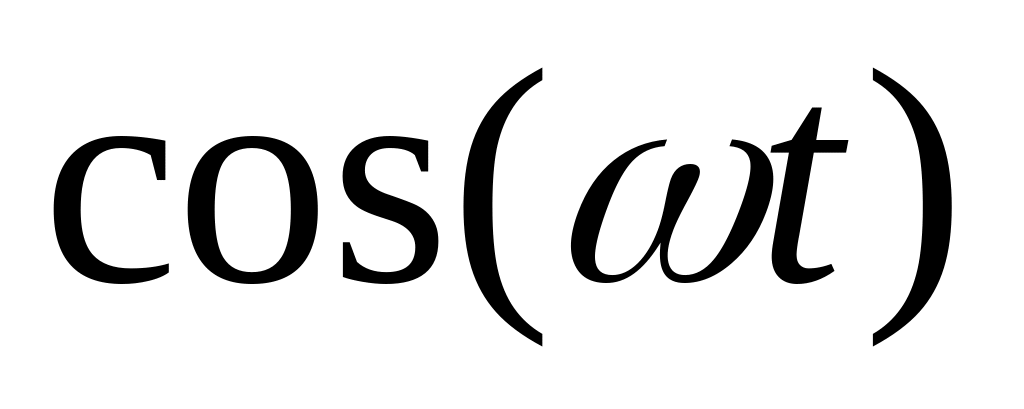

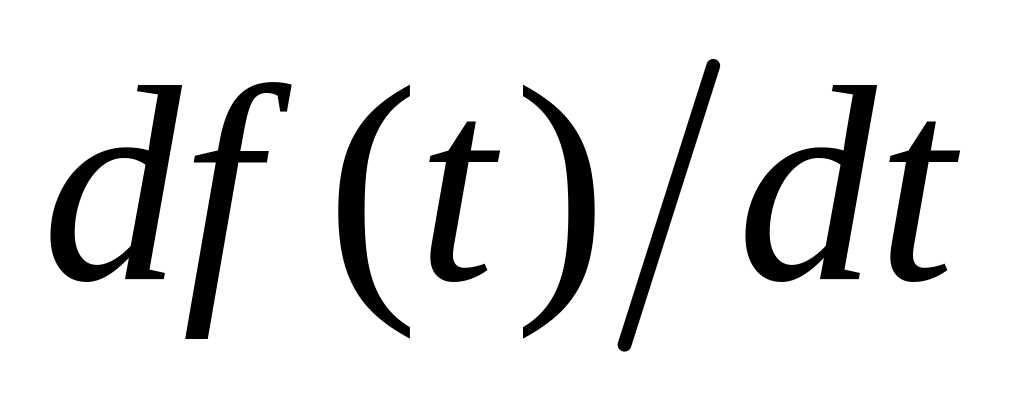
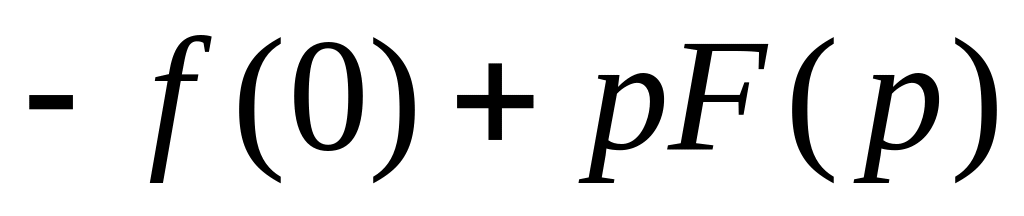
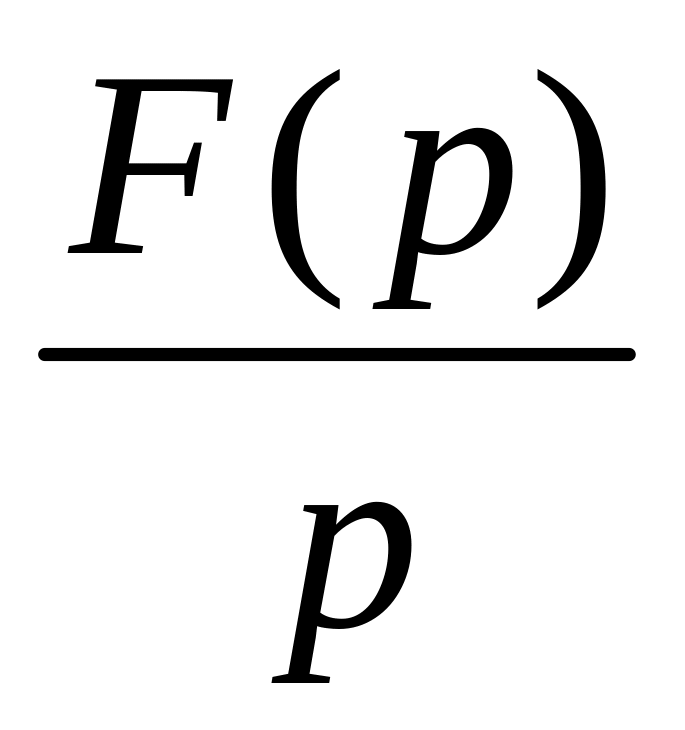
Вернёмся теперь к переходным процессам.
Итак, мы будем сопоставлять каждой
функции его изображение. Например
![]() .
С учётом полученной таблицы можно
сопоставить каждому элементу его
изображение:
.
С учётом полученной таблицы можно
сопоставить каждому элементу его
изображение:
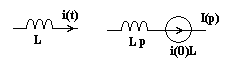
![]()
![]()
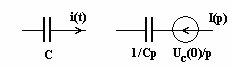
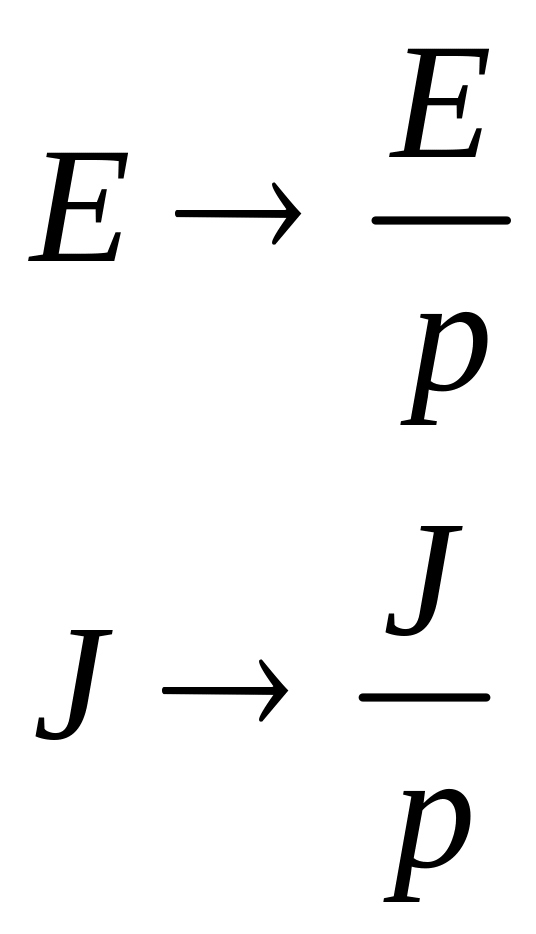
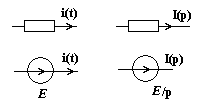
Заметим, что для того, что бы построить
изображение схемы, нужны независимые
начальные условия
![]() .
.
После того как построена схема изображений, в пространстве изображений находятся желаемые токи и напряжения с использованием известных методов расчета (МКирхгофа, МУП, МКТ и т.д.). Для перехода к оригиналу (к временной зависимости) необходимо использовать теорему разложения:
![]() где pk
– корни уравнения
где pk
– корни уравнения
![]()
![]() где pk
– корни уравнения
где pk
– корни уравнения
Пример: Определить ток источника
напряжения если
![]() .
.
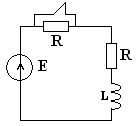
1. Ищем независимые начальные условия
![]()
2. Рисуем операторную схему замещения после коммутации и находим изображение тока
![]()
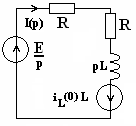 ,
,
где
![]() .
.
Находим корень знаменателя и его
производную
![]() ,
,
![]()
Для определения оригинала используем теорему разложения
![]()
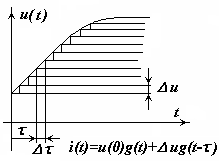
Интеграл Дюамеля
Полный ток в момент t
получаем, если просуммируем все
частичные токи от отдельных скачков
и прибавим их к току
Число членов суммы равно числу
ступенек напряжения. Очевидно, что
ступенчатая кривая тем лучше заменяет
плавную кривую, чем больше число
ступенек. С этой целью заменим конечный
интервал времени
Пример:
Находим переходную проводимость i(t) :
Ищем решения в виде:
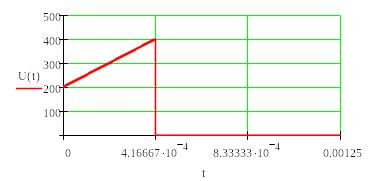
Находим ток на первом интервале i(t) 0 < t < :
Находим ток на втором интервале i(t) t1 < t < ∞ :
|

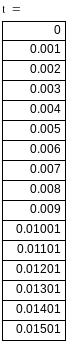
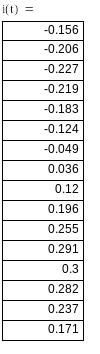
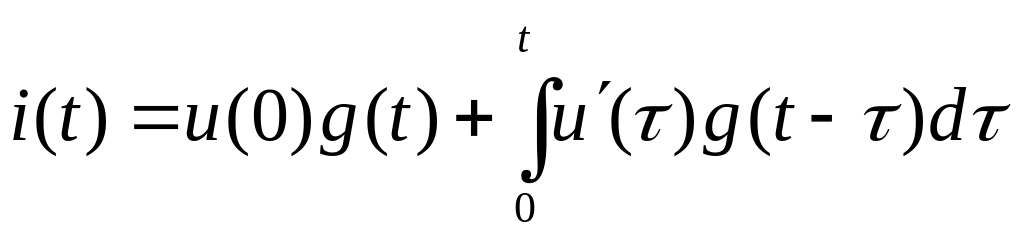 или
или