2.1.4. Порядок выполнения лабораторной работы

1. Кратко описать изучаемые прямые методы безусловной минимизации функций многих переменных.

2. Выполнить алгоритмическую реализацию описанного метода деформируемого многоугольника.

3. Дать геометрическую иллюстрацию указанной преподавателем задачи и выполнить вручную две итерации по составленному алгоритму.

4. Провести с использованием компьютерного комплекса расчеты полученной задачи при различных значениях параметров алгоритма.

5. Проанализировать влияние параметров алгоритма на его сходимость. Дать геометрическую интерпретацию поиска.

6. Сформулировать вывод о влиянии параметров алгоритма на эффективность поиска решения задачи. Содержание работы отразить в отчете.

2.1.5. Задания для лабораторной работы

1. Минимизировать функцию f(X)=2x₁²+x₂²x₁x₂,используя в качестве начального многогранник с вершинами X¹=(2;2)^T, X²=(3;2,5) ^T, X³=(2;3)^T.

2. Минимизировать функцию f(X)=5x₁²+5x₂²+8x₁x₂,используя в качестве начального многогранник с вершинами X¹=(-1;4)^T, X²=(-1;8) ^T, X³=(-3;6)^T.

3. Минимизировать функцию f(X)=4x₁²+x₂²40x₁12x₂+136,используя в качестве начального многогранник с вершинами X¹=(8;9)^T, X²=(10;11)^T, X³=(8;11)^T.

4. Минимизировать функцию f(X)=2x₁²+2x₂²+2x₁x₂14x₁12x₂+29, используя в качестве начального многогранник с вершинами X¹=(6;3)^T, X²=(9;3)^T, X³=(7;4)^T.

5. Минимизировать функцию f(X)=x₁²+4x₂²10x₁48x₂+169, используя в качестве начального многогранник с вершинами X¹=(7;3)^T,X²=(9;1)^T,X³=(9;3)^T.

6. Минимизировать функцию f(X)=x₁²+9x₂²4x₁18x₂+13,используя в качестве начального многогранник с вершинами X¹=(4;3)^T, X²=(6;3)^T, X³=(6;4)^T.

7. Минимизировать функцию f(X)=9x₁²+x₂²36x₁2x₂+37,используя в качестве начального многогранник с вершинами X¹=(5;3)^T, X²=(7;5)^T, X³=(5;5)^T.

8. Минимизировать функцию f(X)=100(x₂x₁²)²+(1x₁)², используя в качестве начального многогранник с вершинами X¹=(-1;1)^T, X²=(-0,5;1)^T, X³=(-1;2)^T.

2.2 Методы покоординатного спуска

Рассмотрим прямые методы решения задачи безусловной минимизации (2.1), использующие вместо итерационных процедур вида (2.3) простейшие вычислительные алгоритмы, основанные на рекуррентной формуле

X^k+1= X^k+ _kS^k, (2.12)

где S^k – направление поиска точки X^k+1 из точки X^k, а положительное число _k – величина шага в этом направлении.

Способ выбора S^k и _k будет определять одну из четырех рассматриваемых далее модификаций метода покоординатного спуска.

2.2.1 Метод циклического покоординатного спуска

Метод циклического покоординатного спуска заключается в изменении каждый раз одной переменной, тогда как другие остаются постоянными. Опишем этот метод для задачи (2.1).

Пусть X⁰– некоторое начальное приближение, а ₀–некоторое положительное число, являющееся параметром алгоритма. Допустим, что уже известны точка X^kÎEⁿ и число _k0 при некотором k0. Обозначим e^j=(0,…,0,1,0,…,0)–единичный координатный вектор, у которого j-я координата равна 1, остальные равны нулю, j=1,…,n. Положим

S^k=e^jk, j_k=kn +1, (2.13)

где  целая часть числа k/n. Условие (2.13) обеспечивает циклический перебор координатных векторов e¹,…,eⁿ, т.е. S⁰=e¹,…, S^n-1=eⁿ, Sⁿ=e¹,…,

S^2n-1=eⁿ, S²ⁿ=e¹….

Вычислим значение функции f(X) в точке X= X^k+ _kS^k и проверим неравенство

f(X^k+ _kS^k)  f(X^k). (2.14)

Если оно выполняется, то полагаем

X^k+1= X^k+ _kS^k, _k+1=_k. (2.15)

В случае, если условие (2.14) не выполняется, вычисляем значение функции f(X) в точке X= X^k _kS^k и проверяем неравенство

f(X^k - _kS^k)  f(X^k). (2.16)

При выполнении условия (2.15) полагаем

X^k+1= X^k - _kS^k, _k+1=_k. (2.17)

Будем считать (k+1)–й этап удачным, если выполнилось хотя бы одно из условий (2.14) или (2.16). Если же ни одно из этих условий не выполнено, считаем (k+1)–й этап неудачным и полагаем

Х^k+1=X^k, _k+1=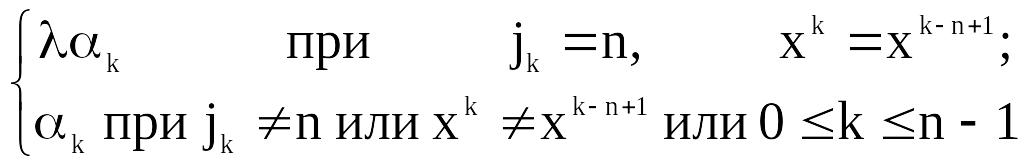 _(2.18)

где (0;1) –фиксированное число, являющееся параметром алгоритма. Условие (2.18) означает, что если за один цикл из n этапов при переборе направлений всех координатных векторов e¹,…,eⁿ с шагом _k реализовался хотя бы один удачный этап, то длина шага _k не дробится и сохраняется на протяжении по крайней мере следующего цикла из n этапов. Если же среди последних n этапов ни одного удачного не оказалось, то шаг _k дробится.

Скорость сходимости данного метода невысока. Несмотря на это, метод циклического покоординатного спуска широко применяется на практике благодаря простоте реализации.

Заметим, что такой метод работает плохо, если в выражение минимизируемой функции входят произведения x _ix _j, т.е. если имеет место взаимодействие между x _i, i=1,…,n.

Указанного в конце предыдущего пункта недостатка можно избежать с помощью следующей модификации метода покоординатного спуска, известной под названием метода Зейделя.