3.2. Метод возможных направлений
3.2.1. Постановка задачи выпуклого программирования
Рассмотрим задачу выпуклого программирования (ЗВП)
(3.10)
Введем обозначения
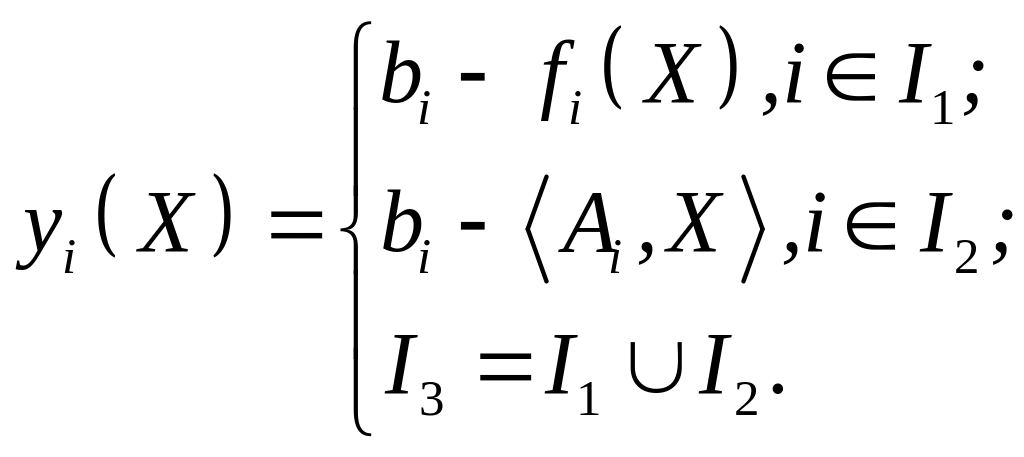(3.11)
Тогда задачу (3.10) можно записать следующим образом
(3.13)
3.2.2. Описание метода возможных направлений
Идея метода заключается в том, что в каждой очередной точке выбирается подходящее направление и производится исчерпывающий спуск в этом направлении.
Направление S
в точке XÎR
называется возможным, если достаточно
малое перемещение из точки Х в этом
направлении не выводит точку за пределы
дополнительной области R. То есть, если
,то
S-возможное
направление в точке ХÎR.
Возможное направление
S
в точке Х называется подходящим, если
перемещение из точки Х в этом направлении
ведет к уменьшению значения функции
,
то есть если
Если в некоторой
точке
не существует подходящих направлений,
то точка
является точкой минимума функции
.
Метод возможных направлений осуществляется следующим образом:
1.Точка начального
приближения выбирается в допустимой
области, т.е.
.
2.Последовательность
точек
,принадлежащих
R, строится так, чтобы выполнялись
неравенства
При этом, строя
точку
так,
чтобы выполнялись неравенства
обнаруживаем, что либо
не ограничена, либо такой точки не
существует, т.е.
оптимальная
точка. В обоих случаях процесс решения
задачи прекращается. Задача решена.
Процедура построения точки состоит из двух этапов:
а) в точке
определяется подходящее направление
;
б)
определяется длина шага
:
,
который надо
выполнить из точки 
в
выбранном направлении
.
3.2.3. Построение начального приближения
Шаг 1.
Строим точку
.
Шаг 2.
Располагая точкой
,
вычисляем значение функции
.
Шаг 3.
Если значение функции
,
то точка
удовлетворяет
линейным ограничениям задачи (1), т.е.
.
Если же значение
,
то в точке
не выполняется условие
и следовательно точка
не удовлетворяет линейным ограничениям
задачи (1).
Шаг 4.
Введем в рассмотрение неотрицательные
числа
,
положив
для тех индексов
,
для которых
и
для тех индексов, для которых
.
Шаг 5.
Вводим дополнительную переменную
,
расширяя тем самым размерность вектора
неизвестных на единицу
и в (n+1)-мерном пространстве формируем
следующую задачу:
(3.14)
Получили
таким образом в (n+1)-мерном пространстве
задачу минимизации линейной
функции
на множестве, задаваемом линейными
ограничениями, т.е. задачу линейного
программирования, которая решается за
конечное число шагов симплекс-методом.
В качестве начального опорного плана
можно выбрать точку
.
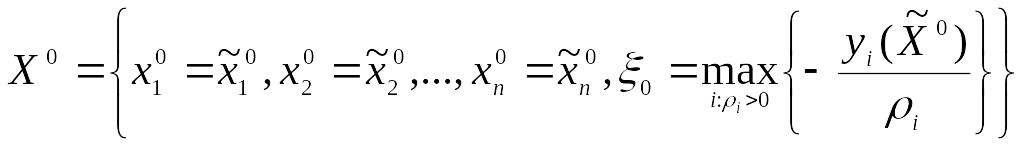В качестве 
можно взять
.
Решая вспомогательную
задачу (3.14) симплекс методом, за конечное
число шагов получим оптимальный план,
в котором
.
Тогда первые n
компонент этого опорного плана определят
точку
,
которая будет удовлетворять всем
линейным ограничениям исходной задачи,
т.е.
.
Шаг 6.
Вычисляем
.
Задаем неотрицательные числа
,
полагая
для тех индексов
,
для которых
и
для тех индексов, для которых
.
Шаг 7.
Формулируем еще одну вспомогательную
задачу, введя дополнительную переменную
, следующим образом:
(3.15)
Это есть ЗВП, для которой известна начальная точка с координатами
.
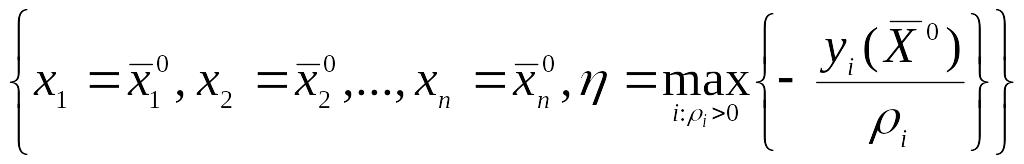Если выбрать в
качестве 
,
тогда начальная точка будет
.Очевидно,
если в ходе решения ЗВП (2) на каком-то
шаге получим
,
т.е. вектор
,
то соответствующий вектор
определит искомую точку
,
которая будет являться начальной точкой
исходной задачи.
Если множество R непусто и регулярно по Слейтеру, то, применяя для задачи (3.15) МВН, получим h=0 за конечное число шагов.
Вместо того, чтобы
последовательно удовлетворять сначала
линейным, а затем нелинейным ограничениям,
можно, избегая шаг5 и шаг6 и имея точку
, сразу сформулировать и решить только
одну задачу
, (3.16)
где
для тех индексов
,
для которых
.
Задача (3.16 ) является ЗВП, для которой за нулевое приближение можно взять точку
.
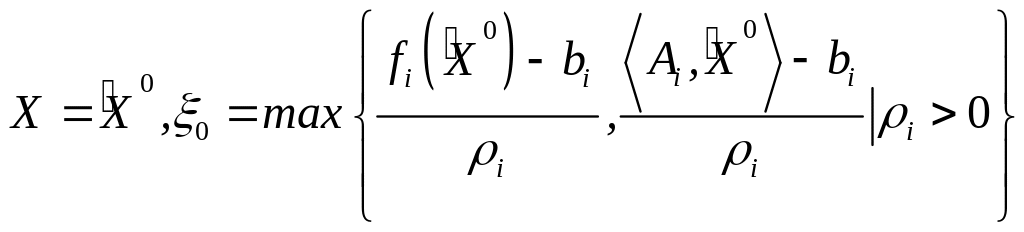Однако, решение задачи (3.16) является более сложным, чем решение задач, которые рассматривались в шаг 5 и шаг 6.