2.2.4. Метод Пауэлла.

В основе этого метода лежит рассмотренный в пункте 2.2.2 метод покоординатного спуска Зейделя, дополненный последовательным нахождением направлений убывания после завершения очередной внешней итерации и минимизацией функции f(X) по этим направлениям.

Пусть задана точка начального приближения X⁰ÎEⁿ. Выполним одну внешнюю итерацию метода покоординатного спуска Зейделя (см. пункт 2.2.2), т.е. найдем точку

Xⁿ= X⁰+

где e^j – единичный координатный вектор, у которого j–я координата равна 1, остальные равны 0, j=1,…,n. При этом величина шага определяется с помощью какой-либо процедуры одномерной оптимизации по 

 _j =arg min {f(X^j-1+ e^j ) ÎR}.

Далее выполняется “диагональный”шаг в направлении убывания функции f(X) по вектору: Sⁿ⁺¹=XⁿX⁰: Xⁿ⁺¹=Xⁿ+_n+1Sⁿ⁺¹, где величина шага _n+1 определяется путем минимизации целевой функции в направлении вектора Sⁿ⁺¹ с помощью одномерного поиска по :

 _n+1 =arg min {f(Xⁿ+Sⁿ⁺¹) | 0}.

Полагая X⁰=Xⁿ⁺¹, приступаем к выполнению следующей внешней итерации. Описанная процедура повторяется до тех пор, пока не выполнится одно из условий (2.19).

2.2.5. Типовые примеры

Пример 1. Решить задачу минимизации функции двух переменных f(X)=5x₁²+5x₂²+8x₁x₂ из начальной точки X⁰=(5;5)^Т методом покоординатного спуска Зейделя.

Заметим, что линии уровня данной целевой функции  соосные эллипсы с центром в начале координат, большая ось которых наклонена под углом 135 к оси х₁. Результаты расчетов по приведенному в пункте 3 алгоритму приведены в таблице и графически проиллюстрированы на рис.5. При нахождении очередной точки X^к минимизирующей последовательности происходит смещение по прямой, параллельной одной из координатных осей, до точки с наименьшим на этой прямой значением функции f(X). Очевидно, эта точка будет точкой касания рассматриваемой прямой и соответствующей линии уровня.

	Таблица 1
	K	X1	X2	F(x)
	0	2	5	225
	1	-4	5	45
	2	-4	3,2	28,8
	3	-2,56	3,2	18,43
	4	-2,56	2,05	11,8
	5	-1,64	2,05	7,55
	6	-1,64	1,31	4,83
	7	-1,05	1,31	3,09
	8	-1,05	0,84	1,98
	9	-0,67	0,84	1,27
	10	-0,67	0,54	0,81

Эффективность прямых методов обычно оценивают или по объему вычислений,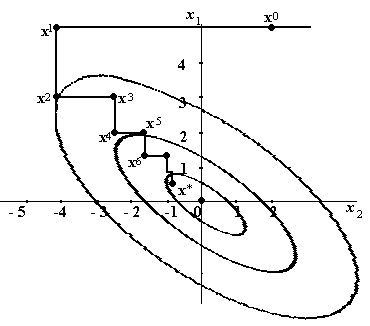

Рис.5. Траектория поиска методом

покоординатного спуска Зейделя(к примеру1).

Пример 2. Решить задачу минимизации функции f(X)=(x₁+1)²+x₂² методом ХукаДживса из начальной точки X⁰=(2;3)^T.

Зададим вектор перемещения =(2;3)^T. Исходное значение функции в начальной точке f(X⁰)=18. В соответствии с алгоритмом, описанным в пункте 4, сначала проводим исследующий поиск из точки X⁰

x₁⁽¹⁾=2+0,5=2,5; f(2,5;3)=21,25 (неудача);

x₁⁽¹⁾=20,5=1,5; f(1,5;3)=15,25 (успех);

x₂⁽¹⁾=3+1=4; f(1,5;4)=22,25 (неудача);

x₂⁽¹⁾=31=2; f(1,5;2)=10,25 (успех).

Исследующий поиск оказался удачным. Теперь из новой точки X¹=(1,5;2)^T перемещаемся в направлении убывания по вектору X¹X⁰ в точку X²=2X¹ X⁰:

x₁⁽²⁾=21,52=1; x₂⁽²⁾=223=1; f(1;1)=5.

Проводим исследующий поиск в точке X¹=(1,5;2)^T:

x₁⁽³⁾=1+0,5=1,5; f(1,5;1)=7,25  f(X²) (неудача);

x₁⁽³⁾=10,5=0,5; f(0,5;1)=3,25  f(X²) (успех);

x₂⁽³⁾=1+1=2; f(0,5;2)=6,25  f(X²) (неудача);

x₂⁽³⁾=11=0; f(0,5;0)=2,25  f(X²) (успех);

Поскольку f(X³)=2,25 f(X¹)=10,25 и перемещение из точки X¹ в точку X²=(1;1)^T успешно, то вновь перемещаемся по направлению убывания из точки X³ в точку

X⁴=2X³ X¹:

x₁⁽⁴⁾=20,51,5=-0,5; x₂⁽⁴⁾=202=-2; f(-0,5;-2)=4,25.

После этого проводим исследующий поиск в точке X⁴=(-0,5;-2)^T:

x₁⁽⁵⁾=-0,5+0,5=0; f(0;-2)=5  f(X⁴) (неудача);

x₁⁽⁵⁾=-0,50,5=-1; f(-1;-2)=4  f(X⁴) (неудача);

x₂⁽⁵⁾=-2+1=-1; f(-0,5;-1)=1,25  f(X⁴) (успех).

Поскольку f(X⁵)=1,25 f(X³)=2,25 и перемещение из точки X³ в точку X⁴ можно признать успешным, то последовательность поисков по направлению убывания продолжаем до тех пор, пока на очередном этапе в конце исследующего поиска значение f(X) не окажется больше, чем в предыдущей точке. Тогда из последней проводим исследующий поиск для определения нового удачного направления. На рис.6 приведена графическая интерпретация этапов поиска. Линии уровня целевой функции f(X)=(x₁+1)²+x₂²– концентрические окружности с центром в точке X*=(-1;0). Пунктиром на рисунке выделены траектории исследующего поиска, сплошными линиями – перемещения в направлении убывания. Убедитесь в соответствии графической иллюстрации описанному алгоритму.

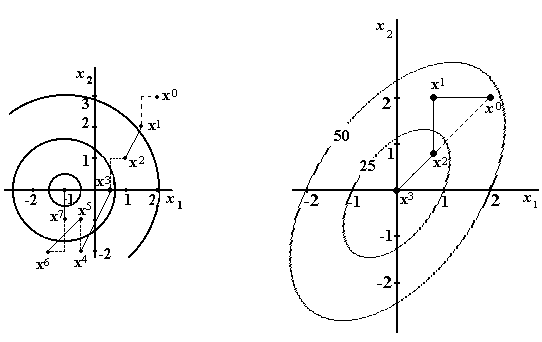
Рис.6. Минимизация функции Рис.7. Минимизация функции методом

методом ХукаДживса (к примеру 2). Пауэлла (к примеру 3).

Пример 3. Рассмотрим графическую иллюстрацию решения задачи минимизации функции f(X)=2x₁²+x₂²x₁x₂ методом Пауэлла из начальной точки X⁰=(2;2)^T(рис.7).

Линии уровня функции f(X) – соосные эллипсы с центром в начале координат, большая ось которых наклонена к оси x₁ под углом 67,5. Первый шаг делается в соответствии с методом покоординатного спуск Зейделя ( см. 2.2.2 ) из точки X⁰ в направлении -e¹=(-1;0), т.е. минимизируется f(X⁰– e¹) по 0 с помощью процедуры одномерного поиска. В результате находится точка X¹=X⁰ ₁e¹, где ₁=arg min{f(X⁰– e¹)|0}. Очевидно, эта точка будет точкой касания с соответствующей линией уровня f(X)=const. Аналогично выполняется второй шаг из точки X¹ в направлении -e²=(0;-1) и находится точка X²=X¹₂e², где ₂=arg min{f(X¹– e²)|0}. Затем выполняется «диагональный» шаг из точки X² в направлении вектора X² X⁰. Поскольку целевая функция f(X) квадратичная, точку её минимума удалось найти точно за конечное число шагов.