4. Приближённое решение задачи оптимального управления

4.1. Постановка задачи оптимального управления

Рассматривается некоторая техническая система, математической моделью которой является гладкая динамическая система с непрерывным временем:

_i=f_i (t, X(t),u (t)), i=1,...,n;tÎ[t₀, t_k]; (4.1)

x_i(t₀)= x_i0 ,i=1,...,n; (4.2)

где X(t)=( x₁(t), x₂(t),…, x_n(t)), u(t)=( u₁(t),…, u_r(t)).

Начальное состояние системы {t₀, X(t₀)} и время перехода t_kt₀ считаются заданными, X(t_k)- свободно.

Качество управления предлагается оценивать интегральным функционалом

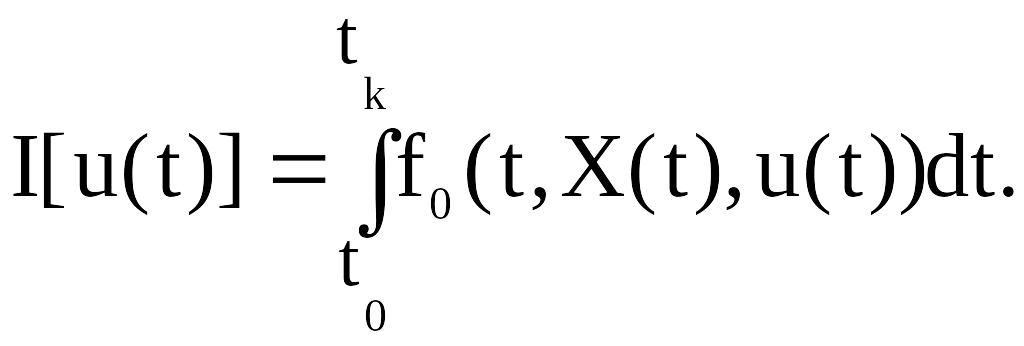(4.3)

Тогда оптимизация рассматриваемой технической системы сводится к решению следующей задачи оптимального управления:

для динамической системы ( 4.I ) найти управление u(t), tÎ[t₀, t_k], переводящее её из заданного начального состояния (4.2) в некоторое конечное состояние за фиксированное время перехода и доставляющее минимум функционалу (4.3).

Предполагая, что функции f_i (t,X(t),u(t)), i=0,...,n непрерывно дифференцируемы по совокупности аргументов X, u, решить поставленную задачу приближенно с помощью градиентного метода первого порядка.

4.2. Градиентный метод решения задачи оптимального управления

4.2.1. Описание градиентного метода в функциональном пространстве.

Градиентный метод является одним из эффективнейших численных методов решения задачи оптимального управления. Он состоит в последовательном “улучшении” некоторого произвольно заданного управления, а именно: на каждом этапе улучшения предыдущее управление исправляется в напрвлении наибыстрейшего приближения к искомому оптимальному управлению.

Перейдем к конструированию алгоритма, реализующего данный метод.

Пусть известно некоторое допустимое управление “нулевого приближения” u=u⁰(t), которому соответствует в силу (4.1), (4.2) фазовая траектория X⁰ (t) и некоторое численное значение функционала I⁰=I[u⁰(t)], вычисленное по формуле (4.3).

Построим новое управление

u(t)=u⁰(t) + du(t), "tÎ[t₀,t_k], (4.4)

где du(t) такова, что норма мала.

Тогда вариация фазовой траектории, вызванная таким равномерно малым изменением управления, будет подчиняться так называемым уравнениям в вариациях

, tÎ[t₀,t_k]; (4.5)

dX(t₀)=0. (4.6)

Интегрирование последних от t= t₀ до t= t_k с введением вспомогательной вектор-функции l(t)=( l₁(t), l₂(t),…, l_n(t)) приводит к следующему результату

(4.7)

Одноко, непосредственное варьирование функционала дает следующее соотношение

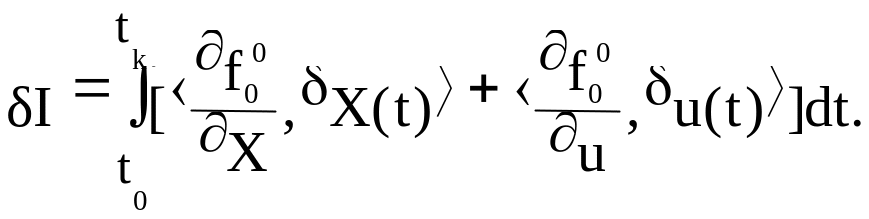(4.8)

Добавим к правой части соотношения (4.8) равное нулю выражение (4.7)

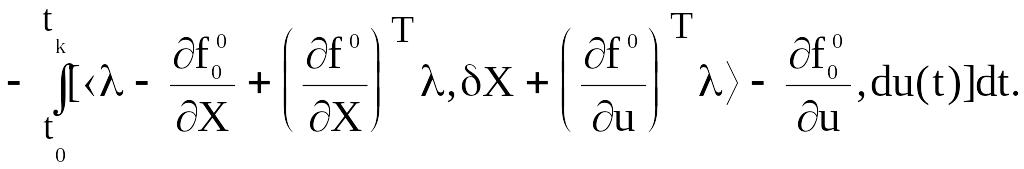
Потребуем, чтобы вектор-функция l(t) удовлетворяла следующим условиям:

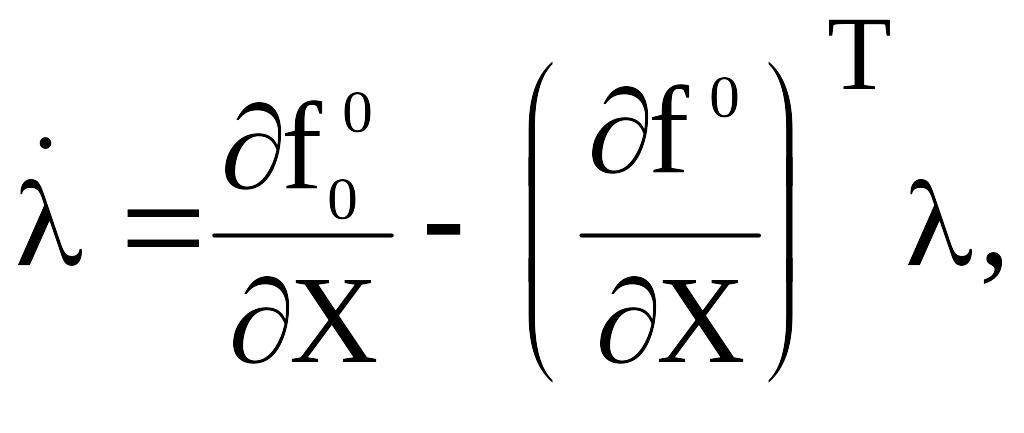"tÎ[t₀,t_k]; (4.9)

l( t_k)=0. (4.10)

Тогда задача построения согласно формулам (4.4) нового “улучшенного” управления сводится к задаче минимизации функционала

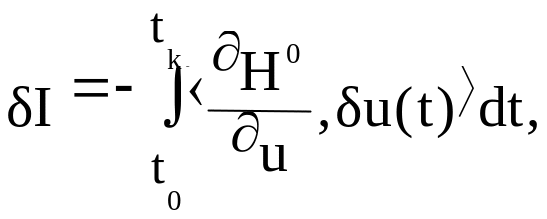(4.11)

где H ₀=H(t, X⁰, u⁰, l)=  f₀ (t, X⁰, u⁰) + < l (t), f₀ (t, X⁰, u⁰)>. (4.12)

Очевидно, что поправки du = (du₁(t), du₂(t),…, du_r(t)), реализующие минимум dI в соответствии с (4.11), должны удовлетворять следующим необходимым условиям:

"tÎ[t₀,t_k]; (4.13)

Таким образом, “улучшенное” управление u(t)=( u₁(t), u₂(t), …, u_r(t)), "tÎ[t₀, t_k ], мы найдем по формулам (4.4), задавая достаточно малые абсолютные значения поправок du_i, i=1,...,r и определяя их знаки по формулам (4.13).

Следует однако отметить, что предложенное правило вычисления поправок du_i, i=1,...,r, "tÎ[t₀, t_k ] не гарантирует обязательного убывания функционала (4.3) на каждом этапе расчета. Это объясняется невозможностью заранее предполагать, что принятым значениям поправок будет соответствовать значение dI, близкое к DI. Поэтому на каждом этапе расчета следует находить DI=I  I⁰ и в случае, если DI³0, расчет следует повторить при уменьшенных |du_i|, i=1,...,r.