4.2.2. Алгоритм метода.

Итак, нами построен алгоритм расчета оптимального управления и соответствующей ему оптимальной траектории в виде следующей последовательности вычислительных операций.

Шаг 1. Задать управление “нулевого” приближения

u⁰(t)=( u₁⁰ (t), u₂⁰ (t), …, u_r⁰ (t)), "tÎ[t₀, t_k ].

Шаг 2. Проинтегрировать от t= t0 до t= tk систему (4.1)

= f_i (t, X(t), u⁰(t)), i=1,...,n ,

с начальными условиями (4.2) методом РунгеКутта с постоянным шагом h. Получить тем самым X⁰(t)=( x₁⁰ (t), x₂⁰ (t), …, x_n⁰ (t)), "tÎ[t₀, t_k ] и значения фазовых координат x_i⁰ (t_k) , i=1,...,n в конечный момент времени t=t_k.

Шаг 3. Вычислить значение функционала (4.3) на управлении “нулевого” приближения

,

Например, по формуле Симпсона

,

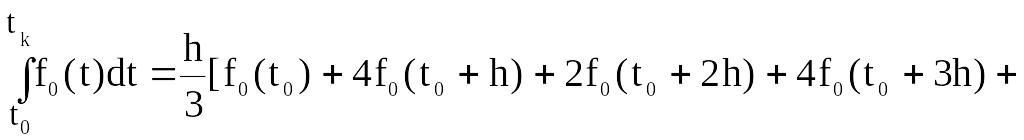
где обязательно должно быть h= .

Вычисление функционала по приведенной формуле можно заменить интегрированием совместно с системой (4.1) уравнения

(t)=f₀ (t, X⁰(t), u⁰(t)), x_n+1 (t₀)=0.

Тогда значение функционала найдется так

I[u⁰(t)] = x⁰_n+1 (t_k).

Шаг 4. Если требуется вычислить функции влияния , i=1,...,r, то следующим выполняется шаг 5, иначе идти к шагу 9.

Шаг 5. Проинтегрировать в направлении от t= t_k до t= t₀ каноническую систему (4.1), (4.9)

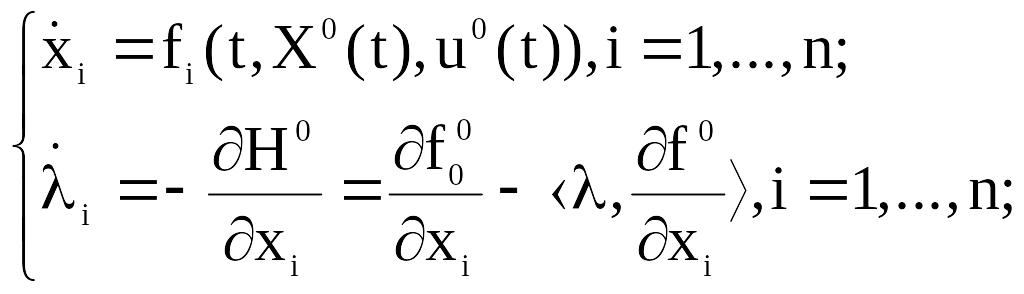
с “начальными” условиями x_i(t_k)= x_ik, i=1,...,n; l_i(t_k)= 0, i=1,...,n; где x_ik, i=1,...,n– полученные на шаге 2 значения фазовых координат в момент времени t_k .

Шаг 6. Вычислить функции влияния

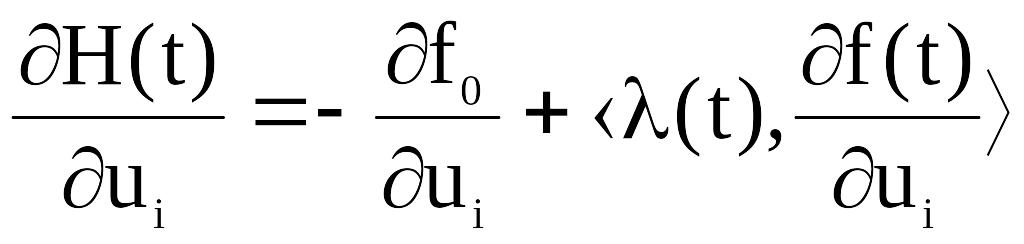, i=1,...,r, "tÎ[t₀, t_k ].

Шаг 7. Вычислить поправки управляющих воздействий

du_i(t)=q×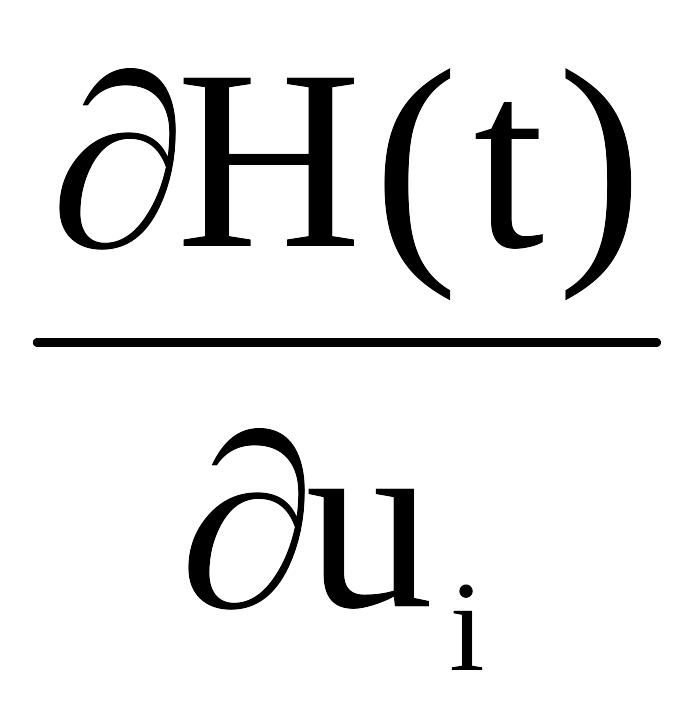 , i=1,...,r, "tÎ[t₀, t_k ],

где q – заранее заданная достаточно малая положительная величина- шаговый коэффициент.

Шаг 8. Вычислить новое “улучшенное” управление

u_i(t)=u_i⁰(t) + du_i(t), i=1,...,r, "tÎ[t₀,t_k]

и приступить к выбору надлежащего значения шагового коэффициента q путем повторения вычислений, начиная с шага 2 (но уже без вычислений функций влияния).

Шаг 9. Сравнить новое значение функционала I=I[u⁰+q ] с его предыдущим значением I⁰=I[u⁰(t)].

Если выполняется условие I0³I, то следует уменьшать шаг

q=b×q, bÎ(0,1)

с последующим вычислением нового управления u(t)=u⁰(t) + q и соответствующего ему значения функционала I до тех пор, пока не будет достигнуто требуемое условие I⁰>I.

Если же уже при начальном значении шагового коэффициента получится I⁰<I, то можно попытаться увеличить шаг

q=a×q, a>1

двигаясь в том же направлении, пока наблюдается уменьшение значения функционала.

Шаг 10. Проверить условие

I[u⁰+du]-I[u⁰] £e,

где e наперед заданное достаточно малое положительное число, определяющее точность результата.

Если условие выполняется, то оптимальное управление найдено и решение задачи следует прекратить; иначе – выполнить следующую итерацию, повторив все вычисления, начиная с шага 2.

4.2.3. Порядок выполнения лабораторной работы.

1. Записать постановку задачи в соответствии с конкретным вариантом задания.

2. Изучив алгоритм градиентного метода первого порядка, записать алгоритм решения своей задачи.

3. Разработать блок-схему программы, реализующей данный алгоритм.

4. Ввести в программу исходные данные, соответствующие своему варианту задания, и получить приближенно оптимальное управление ( u₁(t), u₂(t) ) и траекторию ( x₁(t), x₂(t)).

5. Повторить счет, изменив значения параметров алгоритма q, a, b с целью улучшения процесса сходимости.

6. По результатам счета построить графики x1(t), x2(t), u1(t), u2(t) на первой, одной из промежуточных и последней итерациях.

7. На основании анализа результатов счета сделать вывод об особенностях решения задачи градиентным методом.