1.2.1. Метод дихотомии

Идея этого метода заключается в том, чтобы делить очередной отрезок, содержащий точку минимума функции пополам и исключать из рассмотрения ту часть, где минимума быть не может. Отсюда и название метода – деление отрезка пополам (дихотомия).

Итак, в методе дихотомии пробные точки выбираются близко к середине очередного отрезка [a; b]

x₁= x₂= (1.8)

где d0- некоторое число малое настолько, что ещё можно отличить значения f(x₁) и f(x₂) друг от друга. При этом отношение длин нового и исходного отрезков близко к 1/2:

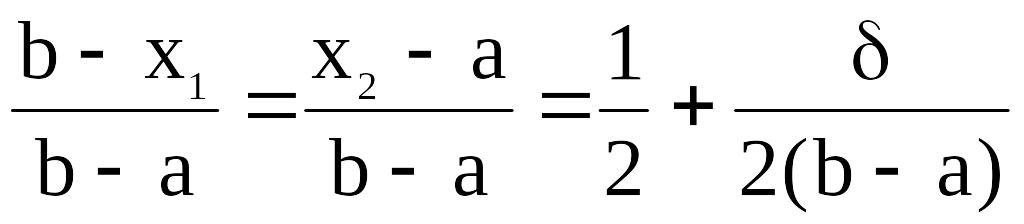(1.9)

Поэтому, чем меньше число d, тем больше относительное уменьшение длины отрезка на каждой итерации. Т.е. при уменьшении d повышается скорость сходимости метода дихотомии. Рекомендуется значение d выбирать из интервала (0;2e).

В конце вычислений по методу дихотомии в качестве приближенного значения х* берут середину последнего из найденных отрезков, убедившись предварительно, что достигнуто неравенство e_n £ e, где

e_n= (1.10)

Находя n из этого условия, получаем число итераций метода дихотомии, необходимое для определения точки х^* с заданной точностью e

n . (1.11)

Опишем алгоритм метода дихотомии.

Шаг 0. Задать параметр точности e > 0, параметр алгоритма dÎ(0;2e).

Шаг 1. Вычислить x1 и x2 по формулам (1.7) и значения функции f(x1) и f(x2).

Шаг 2. Сравнить эти значения. Если f(x₁) £ f(x₂), то перейти к отрезку [a; x2], положив b=x₂, иначе – к отрезку [x₁;b], положив а=x₁.

Шаг 3. Найти достигнутую точность e_n=(b-a)/2. Если e_n > e, то перейти к шагу 1 для выполнения следующей итерации, иначе завершить поиск, положив х^*»(a+b)/2.

1.2.2. Метод золотого сечения

В методе дихотомии при выполнении каждой итерации определяются две новые пробные точки x₁ и x₂. Рассмотрим такое симметричное их расположение на отрезке [a; b], при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением значения функции f(х) только в одной точке, т.к. другое значение уже найдено на предыдущей итерации. Таким свойством обладают точки золотого сечения отрезка [a; b].

Золотым сечением отрезка называется такое деление отрезка на две неравные части, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей частей отрезка. Находятся две точки x₁ и x₂ (x₁ < x₂)

x₁=a+ (b  a); x₂= a+ (b  a), (1.12)

которые делят отрезок [a; b] в указанном отношении

(1.13)

Свойство золотого сечения как раз и замечательно тем, что точка x₁ также производит золотое сечение отрезка [a; x₂], а точка x₂ в том же отношении делит отрезок [x₁;b]. Это свойство и кладется в основу метода золотого сечения.

Отметим, что точки x₁ и x₂ симметричны относительно середины очередного отрезка:

x₁=a+b- x₂; x₂=a+b- x₁. (1.14)

Поэтому на каждой итерации недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке, не используя формул (1.12).

В конце вычислений в качестве приближенного значения х* можно взять середину последнего из полученных отрезков. На каждой итерации отрезок поиска точки минимума уменьшается в одном и том же отношении t=( 1)/2, поэтому в результате n итераций его длина становится равной hn=tn(b  a). Таким образом, точность en определения точки х* после n итераций находится по формуле

e_n = (1.15)

а условием окончания поиска х* c наперед заданной точностью e служит неравенство e_n £ e. Используя это условие и формулу (8) можно оценить число итераций, потребное для достижения заданной точности e:

n ln / ln ln . (1.16)

Опишем алгоритм метода золотого сечения.

Шаг 0. Задать параметр точности e > 0, положить t=( 1)/2.

Шаг 1. Найти x₁ и x₂ по формулам (5). Вычислить f(x₁) и f(x₂). Положить e_n =(ba)/2.

Шаг 2. Проверить условие окончания поиска e_n £ e. Если оно выполняется, то перейти к шагу 4, иначе – к шагу 3.

Шаг 3. Перейти к новому отрезку и новым пробным точкам. Если f(x₁) £ f(x₂), то положить b=x₂, x₂=x₁, f(x₂) = f(x₁), x₁ = b + a  x₂ и вычислить f(x₁), иначе  положить a=x₁, x₁=x₂, f(x₁) = f(x₂), x₂ = a + b – x₁ и вычислить f(x₂). Положить e_n =t×e_n и перейти к шагу 2.

Шаг 4. Завершить поиск, положив х* , f* .