4. Сравнение бесконечно малых величин.

Пусть (х) и (х) - две бесконечно малые величины (то есть стремящиеся к нулю) при хa.

1. Если lim (х)/(х)=0, то говорят, что бесконечно малая  является бесконечно малой более высокого порядка малости по сравнению с бесконечно малой  и пишут =о().

2. Если lim (х)/(х)=m, где m - конечное, отличное от нуля число, то говорят, что  и  - бесконечно малые одного порядка малости и пишут =О(). В частности, если m=1, то бесконечно малые  и  называются эквивалентными. Запись  означает, что  и  - эквивалентные бесконечно малые.

Свойства бесконечно малых.

1. Произведение двух бесконечно малых есть величина бесконечно малая более высокого порядка малости по срав-нению с сомножителями, то есть если =, то =о() и =о().

2. Бесконечно малые  и  эквивалентны тогда и только тогда, когда их разность -= является бесконечно малой более высокого порядка малости по сравнению с  и , то есть если =о() и =о(), то  .

3. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой бесконечно малой эквивалентной ей бесконечно малой, то есть если lim(/)=m и ₁ , ₁ òî lim(₁/₁)=m.

При вычислении пределов полезно применять эквива-лентность следующих бесконечно малых при х0:

sin x  x, tg x  x, arcsin x  x,

arctg x  x, ln(1+x)õ

Пример 1. Сравнить бесконечно малые =tsin²t

è =2tsint ïðè t0.

Решение. Имеем , òî åñòü =î().

Пример 2. Вычислить предел .

Решение. При x0 числитель и знаменатель дроби являются бесконечно малыми. Заменим их эквивалентными бесконечно малыми:

ln(1+3xsinx)3xsinx, tg x²x².

Tîãäà = .

5. Непрерывность функции.

Пусть функция f(x) определена в некоторой окрестности (открытом интервале) точки а и пусть существует предел функции в этой точке . Функция f(x) называется непрерывной в точке а, если предел функции равен значению функции в предельной точке: =f(а). Обозначим х=х-а - приращение аргумента и y=f(х)-f(а) – соответ-ствующее ему приращение функции. На языке приращений непрерывность функции в точке а означает, что бесконечно малому приращению аргумента х соответствует бесконечно малое приращение функции y, то есть y0 при х0.

Функция называется непрерывной на некотором множестве числовой прямой, если она непрерывна в каждой точке этого множества.

Точка, в которой нарушается условие непрерывности функции, называется ее точкой разрыва.

Если в точке а функция имеет конечные пределы слева и справа f(a-0)= , f(a+0)= и при этом не все три числа f(a-0), f(a+0) и f(а) равны между собой, то точка а называется точкой разрыва первого рода. Точки разрыва первого рода, в свою очередь, подразделяются на точки устранимого разрыва, когда f(a-0)=f(a+0)f(а), и точки неустранимого разрыва, когда f(a-0)f(a+0). В последнем случае разность f(a-0)-f(a+0) называется скачком функции в точке а.

Точки разрыва, которые не являются точками разрыва первого рода, называются точками разрыва второго рода. В таких точках не существует хотя бы одного одностороннего предела функции.

Непрерывные на замкнутом интервале [a,b] функции обладают рядом полезных свойств:

1. Непрерывная на замкнутом интервале функция достигает на этом интервале своего наибольшего и наименьшего значений. То есть существуют такие точки x_M, x_m[a,b], ÷òî

f(x_M)= =M è f(x_m)= =m.

2. Непрерывная на замкнутом интервале функция прини-мает все промежуточные значения. То есть для любого числа y[m,M] найдется число х[a,b] такое, что y=f(x).

Все основные эле-ментарные функции непрерывны в каж-дой точке своей об-ласти определения.

Пример. Исследовать на непрерывность функцию

f(x)= .

Решение. Наша функция есть элементарная функция вида а^g(x), которая непрерывна в каждой точке своей области определения. Эта функция определена на всей числовой оси за исключением точки х=-3. Исследуем функцию на непрерывность в этой точке. Если x<-3. то 3/(x+3)<0, поэтому

f(-3-0)=

Если x>-3, то 3/(x+3)>0, поэтому

f(-3+0)= .

Таким образом, в точке х=-3 не существует правостороннего предела функции и, значит, эта точка является точкой разрыва второго рода.

Задача 11. Исследовать на непрерывность функцию. В случае наличия точек разрыва определить тип разрыва и изобразить поведение функции в окрестности точки разрыва.

N	Функции	N	Функции
1	y= ; y=	6	y= ; y=
2	y= ; y=	7	y= ; y=
3	y= ; y=	8	y= ; y=
4	y= ; y=	9	y= ; ó=
5	y= ; y=	10	y= ; y=

Глава 3. Дифференциальное исчисление

функций одной независимой

переменной.

1. Дифференцирование явных функций.

Пусть S(t) означает путь, пройденный телом за время t.Рассмотрим произвольный фиксированный момент времени t и малый временной интервал t. Тогда число есть средняя скорость движения тела на временном интервале [t,t+t]. Ясно, что чем меньший временной интервал мы будем рассматривать, тем точнее соответствующая средняя скорость будет приближаться к величине мгновенной скорости движения в момент времени t

Пусть х₁ è õ₂ - два значения аргумента, а у₁=f(x₁) è ó₂=f(x₂) - соответствующие им значения функции у=f(x). Разность х=х₂-õ₁ называется приращением аргумента, а разность

ó=ó₂-ó₁=f(x₂)-f(x₁)

- соответствующим ему приращением функции.

Производной от функции у=f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

(производная обозначается также f'(x), либо .)

Геометрически значе-ние производной в точке х представляет собой угловой коэф-фициент (тангенс уг-ла наклона) касатель-ной к графику функ-ции у=f(x) в точке с абсциссой х:

y'=f'(x)=k=tg.

Действительно, для фиксированного х отношение y/х представляет собой тангенс угла, образованного секущей АВ с положительным направлением оси ОХ:

Ясно, что при х0 секущая АВ приближается к касательной к графику функции в точке А и при этом Тем самым,

Как уже отмечалось, s=f(t) - путь, пройденный телом за время t, то производная v(t)=s'(t) этой функции в точке t есть скорость тела в момент времени t.

Процедура вычисления производной называется диф-ференцированием функции а функции, имеющие производную в каждой точке своей области определения, - диффе-ренцируемыми функциями. Если функция у=f(x) имеет производную в некоторой точке х, то это означает, что при х0 существует и конечен предел отношения y/х. Это в свою очередь означает, что этой точке приращение функции должно стремить к нулю при х0. Тем самым всякая дифференцируемая функция является непрерывной. Обратное утверждение, вообще говоря, не верно: функция у=х непрерывна на всей числовой оси, но в точке х=0, как легко проверить, не имеет производной.

Формулы дифференцирования основных функций:

1.	11.
2.	12.
3.	13.
4.	14.
5.	15.
6.	16.
7.	17.
8.	18.
9.	19.
10.

Гиперболические функции - гиперболический синус shx, косинус chx, тангенс thx и котангенс cthx, определяются так:

, , , .

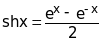Основные правила дифференцирования.

Пусть С - постоянная, u=u(x) и v=v(x) - функции, имеющие производные. Тогда:

1. C^'=0.

2. x'=1.

3. (uv)'=u'v'.

4. (Cu)'=Cu'.

5. (uv)'=u'v+uv'.

^{6. .}

7. Если y=f(u) и u=u(x), то есть y=f(u(x)) - сложная функция переменного х, и при этом функции f(u) и u(x) имеет производные, то справедливо правило дифферен-цирования сложной функции:

.

Если операцию дифференцирования (вычисления произ-водной) обозначать с помощью дифференциалов, то это правило запишется так:

.

Пример 1. y=2x³-4x²+8x-11.

Решение. y'=(2x³)'-(4x²)+(8x)'-(11)'=

=23x²-42x+81-0= 6õ²-8x+8.

Пример 2. y=x²e^x.

Решение. Наша функция есть произведение двух функций u=x² è v=e^x, поэтому применим правило дифференцирования произведения двух функций:

y^'=(x²)'e^x+x²(e^x)'=2xe^x+x²e^x=e^x(2x+x²).

Пример 3. y= .

Решение. По правилу вычисления производной частного двух функций

Пример 4. y=(4x⁵+7)⁴.

Решение. Обозначим u=4x⁵+7, тогда наша функция имеет вид y=u⁴ и по правилу дифференцирования сложной функции имеем:

.

Пример 5.

Решение.

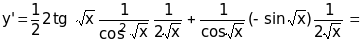
Пример 6.

Решение. У нашей функции как основание, так и показатель степени являются функциями переменной х. Для вычисления производной такой функции предварительно найдем логарифмы левой и правой частей:

.

Равенство функций влечет равенство их производных:

В левой части последнего равенства стоит производная сложной функции ln(y(x)), значит (lny)'=y'/y. Производ-ную в правой части вычислим, как производную произве-дения двух функций:

Следовательно,

=

откуда

Прием, который мы применили в предыдущем примере, (его с некоторой степенью условности называют "лог-арифмическим дифференцированием") позволяет не только вычислить производную функции вида (f(x))^g(x), но и существенно облегчить процедуру вычисления производной некоторых элементарных функций.

Пример 7. y=

Решение.

,

откуда

,

.

Следовательно,

=

= .