7. Плоскость и прямая.

Пусть в пространстве задан вектор N(A,B,C) и точка M₀(x₀,y₀,z₀). Пусть далее Р - плоскость, проходящая через точку М₀ и перпендикулярная вектору N, и M(x,y,z) - произвольная точка этой плоскости. Тогда вектор Ì₀Ì=r(M)-r(M₀)=(x-x₀)i+(y-y₀)j+(z-z₀)k будет перпенди-кулярен вектору N и, значит, скалярное произведение этих векторов должно быть равно нулю:

A(x-x₀)+B(y-y₀)+C(z-z₀)=0.

Тем самым, мы получили уравнение плоскости Р. Если обозначить D=-(Ax₀+By₀+Cz₀), то уравнение плоскости за-пишется в виде :

Ax+By+Cz+D=0.

Его называют общим урав-нением плоскости.

Частные случаи расположения плоскости:

А=0 - параллельна оси ОХ:

Â=0 - îñè ÎÓ:

Ñ=0 - îñè OZ;

D=0 -проходит через начало системы координат:

А=В=0 - перпендикулярна оси OZ;

A=C=0 - îñè ÎÓ:

Â=Ñ=0 - îñè ÎÕ:

А=D=0 - проходит через ось ОХ:

Â=D=0 - îñü ÎÓ:

Ñ=D=0 - îñü OZ;

A=B=D=0 - совпадает с плоскостью ХОУ:

À=Ñ=D=0 - XOZ;

B=C=D=0 - YOZ.

Если в общем уравнении плоскости слагаемое D отлично от нуля, то, разделив обе части уравнения на -D, уравнение плоскости можно привести к виду:

Его называют уравнением плоскости в отрезках, поскольку в нем а, в, и с - величины отрезков, отсекаемых плоскостью Ax+By+Cz+D=0 на осях ОХ, ОУ и OZ соответственно.

Угол между думя плоскостями

A₁õ+B₁ó+C₁z+D₁=0 è A₂x+B₂y+C₂z+D₂=0

(как угол между их нормалями) определяется из формулы:

.

Условие параллельности плоскостей

есть ничто иное, как условие параллельности их нормалей (пропорциональность компонент нормалей), а условие пер-пендикулярности плоскостей

A₁A₂+B₁B₂+C₁C₂=0

- условие перпендикулярности их нормалей (равенство нулю скалярного произведения этих векторов).

Расстояние от точки M₀(x₀,y₀,z₀) до плоскости Ax+By+Cz+D=0 определяется по формуле:

Уравнение плоскости, проходящей через три заданные точки M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂) è M₃(x₃,y₃,z₃), имеет вид:

Прямая линия может быть задана, как линия пересечения двух плоскостей:

A₁õ+B₁ó+C₁z+D₁=0,

A₂x+B₂y+C₂z+D₂=0.

Уравнения прямой, проходящей через две заданные точки M₁(x₁,y₁,z₁) è M₂(x₂,y₂,z₂) имеют вид:

.

Если знаменатели дробей в последних уравнениях обозначить соответственно через l, m и n, то получим уравнение прямой в виде

.

Эти уравнения называются каноническими уравнениями прямой. Они определяет прямую, проходящую через точку M₁(x₁,y₁,z₁) и параллельную вектору S(l,m,n). Этот вектор называется направляющим вектором прямой.

Если общее значение последних равенств обозначить через t, то получим уравнения прямой в параметрическом виде:

.

При изменении параметра t от начального значения t=0 точка пространства с координатами (x(t),y(t),z(t)) перемещается по прямой, отправляясь от своего начального положения - точки М₀.

Угол между двумя прямыми, заданными своими каноническими уравнениями

,

как угол между их направляющими векторами S₁(l₁,m₁,n₁) è S₂(l₂,m₂,n₂), определяется по формуле

.

Параллельность и перпендикулярность прямых означает, соответственно параллельность и перпендикулярность их направляющих векторов S₁ è S₂. В первом случае - это пропорциональность компонент этих векторов, а во втором - равенство нулю их скалярного произведения. Там самым, условие параллельности прямых имеет вид:

,

а условие их перпендикулярности -

l₁l₂ + m₁m₂ + n₁n₂ = 0

Пусть две прямые заданы своими направляющими векто-рами S₁ è S₂ и лежащими на них точками M₁ è M₂. Эти прямые тогда и только тогда лежат в одной плоскости (компланарны), когда в одной плоскости лежат направляющие векторы S₁ è S₂ этих прямых и вектор Ì₂Ì₁. В такой ситуации смешанное произведение этих трех векторов должно быть равно нулю. Значит, условие компланарности двух прямых имеет вид:

Если направляющие векторы двух прямых S₁ è S_{2 ­}не параллельны, то последнее соотношение является необходимым и достаточным условием пересечения прямых в пространстве.

Угол между прямой и плоскостью Ax+By+Cz+D=0, как угол между направляющим вектором S(l,m,n) прямой и нормалью N(A,B,C) плоскости, определяется по формуле:

.

Условие параллельности прямой и плоскости:

Al+Bm+Cn=0.

Условие перпендикулярности прямой и плоскости:

Для определения точки пересечения прямой с плоскостью Ax+By+Cz+D=0, необходимо уравнение прямой представить в парамет-рическом виде x(t)=lt+x₁, y(t)=mt+y₁, z(t)=nt+z₁. Затем текущие координаты x, y и z, как функции параметра t, подставить в уравнение плоскости и, разрешив его, найти то значение параметра t, при котором прямая пересекает плоскость.

Пример 1. Составить уравнение плоскости, проходящей через точки A(2,-1,4) и B(3,2,-1) и перпендикулярной плоскости x+y+2z-3=0.

Решение. Нормаль N(A,B,C) искомой плоскости должна быть перпендикулярна вектору

ÀÂ=(3-2)i+(2+1)j+(-1-4)k=-i+3j-5k

и нормали N(1,1,2) данной плоскости. Поэтому в качестве нормали N(A,B,C) мы можем взять векторное произведение этих векторов:

N(A,B,C)=N(1,1,2)ÀÂ= .

Теперь остается написать уравнение плоскости, проходящей через заданную точку (например А) и перпендикулярной заданному вектору:

11(x-2)-7(y+1)-2(z-4)= 0, èëè 11x-7y-2z-21=0.

Пример 2. Составить уравнение плоскости, проходящей через точку A(5,4,3) и отсекающей на осях системы коор-динат равные отрезки.

Решение. Если плоскость отсекает на осях системы координат отрезки длины а, то ее уравнение имеет вид: x/a+y/a+z/a=1. Так как точка А лежит на искомой плоскости, то ее координаты удовлетворяют уравнению плоскости, поэтому должно выполняться равенство 5/a+4/a+3/a=1, откуда а=12. Следовательно, искомая плоскость имеет уравнение x+y+z-12+0.

Пример 3. Найти расстояние между двумя скрещиваю-щимися прямыми

è

Решение. Первая прямая проходит через точку M₁(1,-3,2) и имеет направляющий вектор S₁(2,1,-3), вторая - через точку M₂(-3,2,-5) и имеет направляющий вектор S₂(-1,-2,1). Найдем объем параллелепипеда, построенного на векторах S₁, S₂ è Ì₂Ì₁=4i+5j+7k:

V=S₁S₂Ì₂Ì₁=

Теперь найдем площадь основания параллелепипеда, построенного на векторах S₁è S₂. Для этого вычислим векторное произведение этих векторов:

S₁S₂=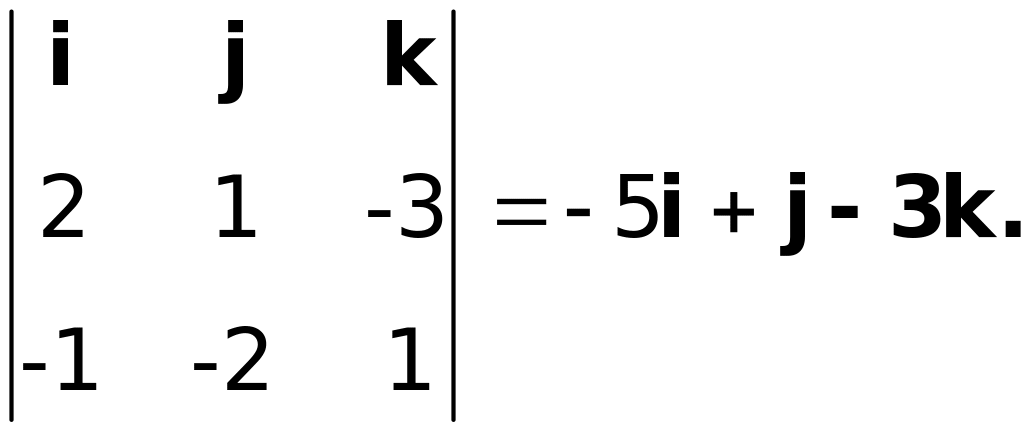

Тогда

S_ïàð=S₁S₂=

Значит, расстояние между нашими прямыми, как высота соответствующего параллелепипеда, равно

d= V/S_ïàð=46/

Пример 4. Найти точку N, симметричную точке М(1,1,1) относительно плоскости x+y-2z-6=0.

Решение. Составим уравнение прямой, проходящей через точку М и перпендикулярной заданной плоскости. Так как прямая перпендикулярна плоскости, то ее направляющий вектор S параллелен вектору нормали N плоскости, поэтому мы можем считать, что S=N=i+j-2k. Так как прямая проходит через точку М, то ее уравнение имеет вид:

Найдем проекцию точки М на плоскость, решив совместно уравнения прямой и плоскости:

, x+y-2z-6=0

Для этого запишем уравнение прямой в параметрическом виде: x=t+1, y=t+1, z=-2t+1. Подставим эти значения координат в уравнение плоскости, найдем t=1, откуда x=2, y=2, z=-1.

Поскольку точка плоскости с координатами (x,y,z) является серединой отрезка MN, то x=(x_M+x_N)/2, y=(y_M+y_N)/2, z=(z_M+z_N)/2, откуда x_N=3, y_N=3, z_N=-3.

Задача 8. Даны точки A, B, C, D (см. предыдущую задачу), плоскости P₁, P₂ и прямые l₁, l₂, l₃

Найти:

1. Уравнение плоскости треугольника АВС.

2. Уравнения плоскостей, проходящих

через прямые l₁, l₂ è прямые l₁, l₃.

3. Уравнение плоскости, проходящей через

точку А и перпендикулярной плоскостям

P₁ è P_2.

4. Уравнение плоскости, проходящей через

прямую l₁ и перпендикулярную плоскости

Ð₁.

5. Уравнение медианы треугольника АВС,

проходящей через вершину В.

6. Уравнение прямой, проходящей через

точку А и перпендикулярной плоскости Р₁

7. Уравнение прямой, проходящей через

точку А и параллельной прямой CD.

8. Проекцию точки А на плоскость Р₁.

9. Уравнение плоскости, проходящей через

точку А параллельной плоскости Р₁.

10. Расстояние между скрещивающимися

прямыми AB и ВС.

N		Условия
1	p1,p2 l1,l2,l3	x+y-3-1=0 4x+3y-z-5=0
2	p1,p2 l1,l2,l3	x+2y-5z-1=0 x-2y+3z-9=0
3	p1,p2 l1,l2,l3	x+3y+z+2=0 x-y-3z-2=0
4	p1,p2 l1,l2,l3	x+y-z=0 x-y-5z-8=0
5	p1,p2 l1,l2,l3	2x+3y-z-4=0 3x-5y+2z=1=0
6	p1,p2 l1,l2,l3	x+2y-z-6=0 2x-y+z+1=0
7	p1,p2 l1,l2,l3	2x+y+z-2=0 2x-y-3z+6=0
8	p1,p2 l1,l2,l3	x-3y+2z=2=0 x+3y+z+14=0
9	p1,p2 l1,l2,l3	2x+3y+z-4=0 2x-2y-z-8=0
10	p1,p2 l1,l2,l3	5x+y-3z+4=0 x-y+2z+2=0