
- •Оглавление
- •Глава 1. Линейная алгебра и аналитическая 5
- •Глава 2. Введение в математический анализ. 55
- •Глава 3. Дифференциальное исчисление 74
- •Глава 4. Дифференциальное исчисление функций нескольких независимых переменных. 108
- •2. Прямоугольные и полярные координаты на плоскости.
- •3. Прямая линия.
- •4. Кривые второго порядка.
- •5. Преобразование координат и упрощение уравне- ний кривых второго порядка.
- •6. Векторы.
- •7. Плоскость и прямая.
- •Глава 2. Введение в математический анализ.
- •1. Функции одной независимой переменной.
- •2. Преобразования графиков функций.
- •3. Пределы.
- •4. Сравнение бесконечно малых величин.
- •5. Непрерывность функции.
- •2. Производная неявно и параметрически заданных функций.
- •3. Приложения производной к задачам геометрии и механики.
- •4. Производные высших порядков.
- •5. Дифференциал.
- •6. Теоремы о дифференцируемых функциях.
- •7. Возрастание, убывание и экстремум функции.
- •8. Выпуклость, вогнутость и точки перегиба.
- •9. Асимптоты.
- •10. Построение графика фyнкции.
- •Глава 4. Дифференциальное исчисление функций нескольких независимых переменных.
- •1. Область определения и поверхности уровня функции.
- •2. Производные и дифференциалы.
- •3. Дифференцирование сложных функций.
- •4. Производная по направлению и градиент.
- •5. Касательная плоскость и нормаль к поверхности.
- •6. Экстремум функции двух переменных.
- •Справочник по элементарной математике
- •Литература
2. Производная неявно и параметрически заданных функций.
Пусть уравнение F(x,y)=0 определяет у как функцию переменного х. В таком случае говорят о неявно заданной функции у=у(х). Будем считать, что эта функция имеет производную. Продифференцировав по переменной х обе части уравнения F(x,y(x))=0, получим уравнение первой степени относительно y'. из которого легко находится производная y'.
Если функция у=у(х) задана параметрическими уравнениями x=x(t), y=y(t), то ее производная y'x опреде-ляется так:
![]()
Если в записи производной употреблять знак дифферен-циала, то это представление выглядит так:

Пример
1.
Найти производную
![]() из уравнения х2+ó2=4.
из уравнения х2+ó2=4.
Решение. Так как у является функцией переменного х, то будем рассматривать у2=(ó(õ))2 как сложную функцию от х. Тогда (y2)'=2yy'и, продифференцировав обе части уравнения по х, получим 2х+2yy'=0, òî åñòü ó'=-x/y.
Пример 2. Найти , если x=t3+3t+1,
y=3t5+5t3+1.
Решение. Последовательно находим
![]() ,
,
откуда
![]() .
.
Задача 12. Вычислить производные функций.
1 |
y= |
|
2 |
y= |
|
3 |
y= |
|
4 |
y= |
|
5 |
y= |
|
6 |
y= |
|
7 |
y= |
|
8 |
y= |
|
9 |
y= |
|
10 |
y= |
|
3. Приложения производной к задачам геометрии и механики.
Если кривая задана уравнением y=f(x), то значение производной функции f'(x) в точке х0 есть угловой коэф-фициент (тангенс угла наклона) касательной, проведенной к графику функции y=f(x) в точке (х0,f(x0)). Значит, уравнение касательной, проведенной к графику функции y=f(x) в точке (х0,f(x0)), имеет вид:
y-f(y0)=f'(x0)(x-x0).
Нормалью к кривой называется прямая линия, перпенди-кулярная касательной и проходящая через точку касания. Из уравнения касательной и условия перпендикулярности прямых получаем уравнение нормали к графику функции y=f(x) в точке (х0,f(x0))
y-y0=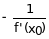 (x-x0).
(x-x0).
Как уже отмечалось, если f(t) - путь, пройденный точкой за время t, то производная f'(t) есть скорость точки в момент времени t.
Пример 1. Составить уравнение касательной и нормали к кривой х2+2õó2+3ó4=6 в точке М(1,-1).
Решение. Из уравнения кривой найдем ее производную 2х+2у2+2õ2óó'+12y3y'=0, òî åñòü
ó'= .
.
Теперь вычислим значение этой производной при х=х0=1 è ó=ó0=-1:
 .
.
Уравнение касательной:
![]()
Уравнение нормали:
![]()
Пример 2. На параболе у2=8х найти точку, в которой касательная к параболе параллельна прямой у=х. Составить уравнения касательной и нормали к параболе в этой точке.
Решение. Координаты требуемой точки обозначим через х0 è ó0. Уравнение любой прямой, проходящей через эту точку имеет вид
ó-y0=k(x-x0),
где k - угловой коэффициент прямой. Tак как касательная должна быть параллельной прямой у=х, то из условия параллельности прямых необходимо, чтобы k=1. С другой стороны, угловой коэффициент касательной к кривой в точке равен значению ее производной в этой точке. Дифферен-цируя уравнение параболы, получим 2уу'=8, или у'=4/y. Тем самым, приходим к равенству
1=k=ó'(õ0)=4/y(x0)=4/y0,
откуда у0=4. Поскольку требуемая точка лежит на параболе, то ее координаты удовлетворяют уравнению параболы: (у0)2=8õ0. откуда х0=2. Следовательно, условию задачи удовлетворяет точка М0(2,4); уравнения касательной и нормали к параболе в этой точке соответственно имеют вид
ó-4=õ-2, èëè õ-ó+2=0, ó-4=-1(õ-2), èëè õ+ó-2=0.
Пример 3. Зависимость пройденного пути от времени при прямолинейном движении точки задается уравнением s(t)=t5/5+(2/)sin(t/8). Определить скорость движения в конце второй секунды.
Решение.
Находим производную пройденного пути
по вре-мени s'(t)=t4+(1/4)cos(t/8).
При t=2 имеем v(2)=s'(2)= =16+![]() .
.

 ;
y2=x+eyarctgx;
;
y2=x+eyarctgx;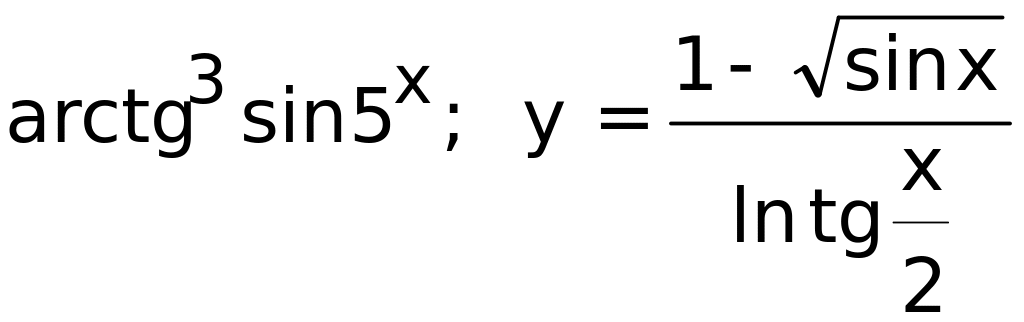 ;
x/y=x-eyarctgx;
;
x/y=x-eyarctgx; ;
ey-x+exy=tgxy;
;
ey-x+exy=tgxy;