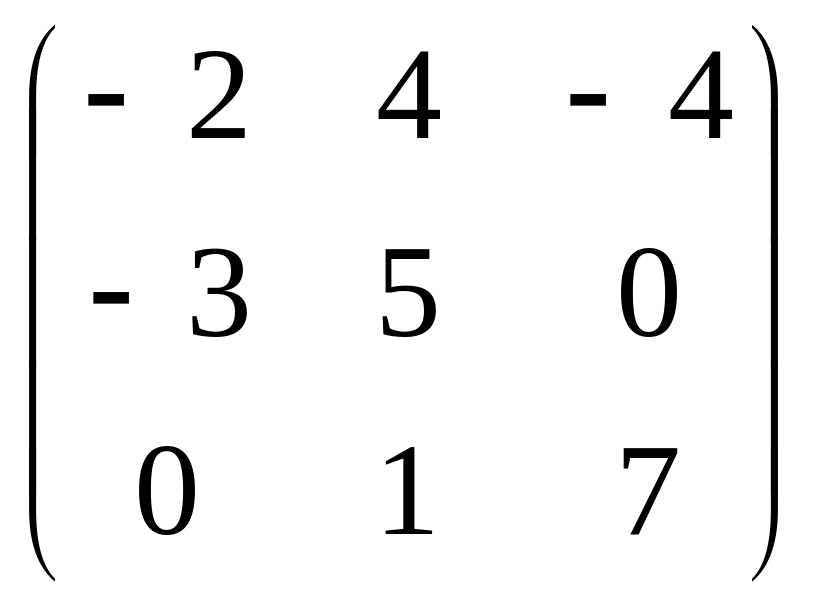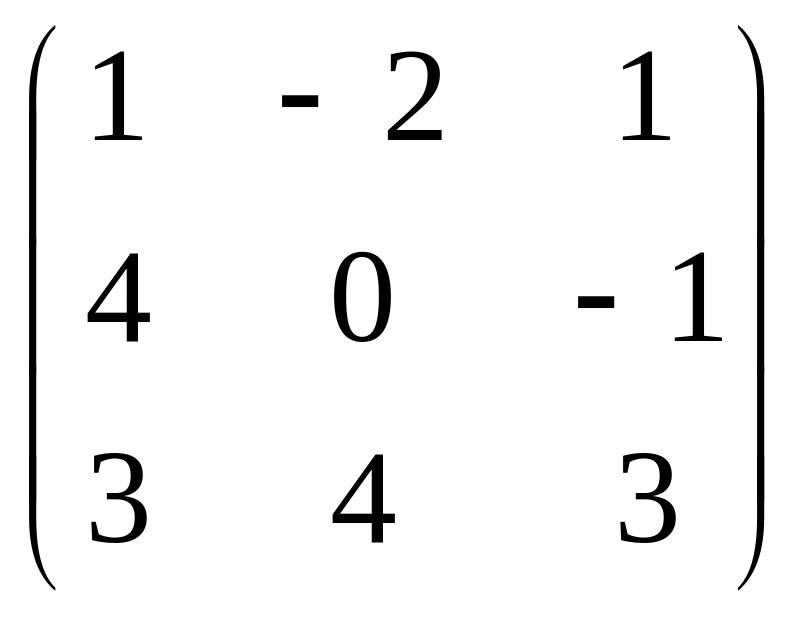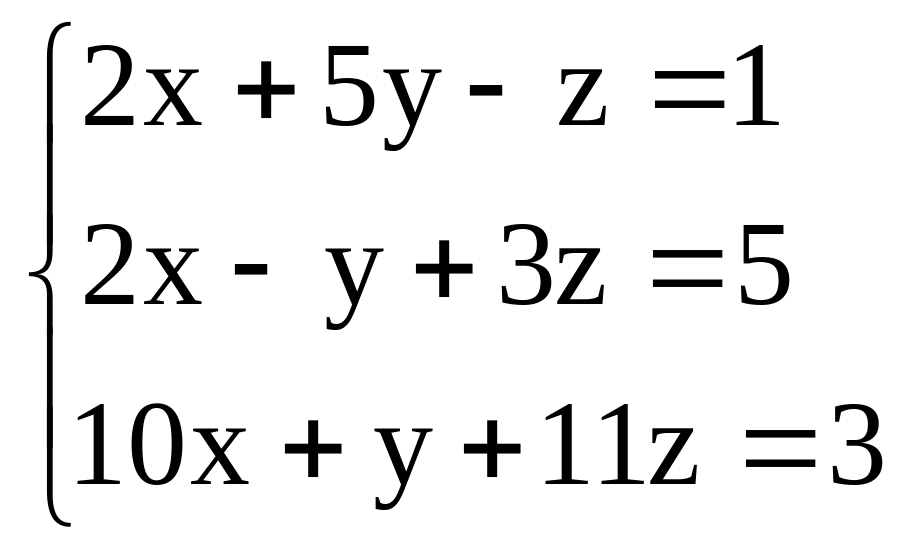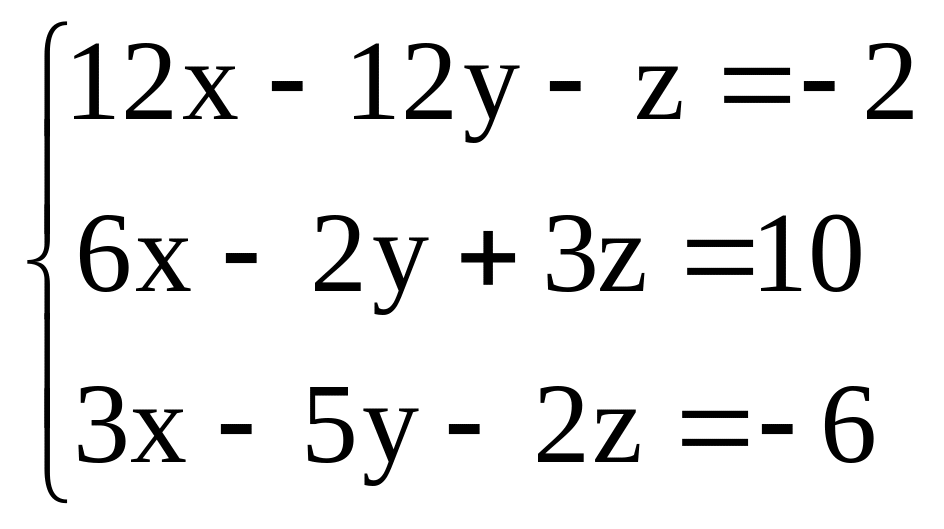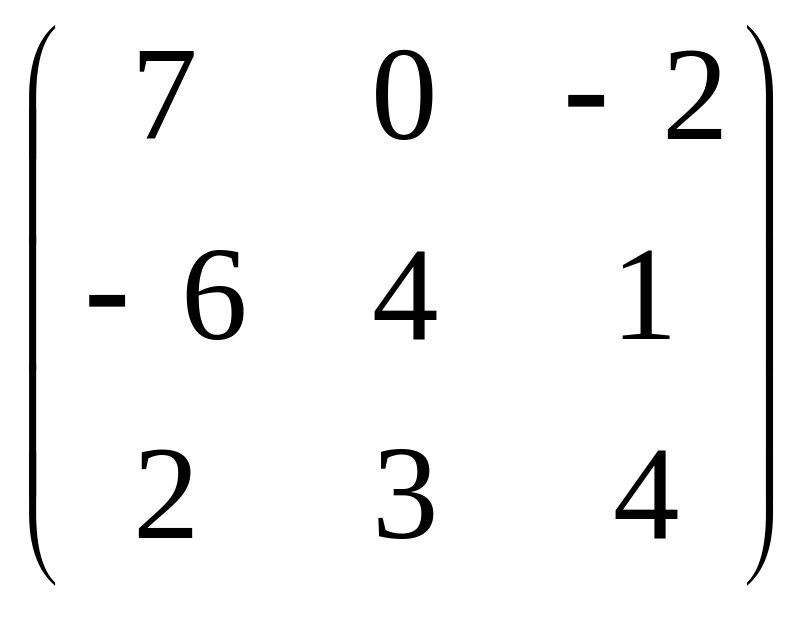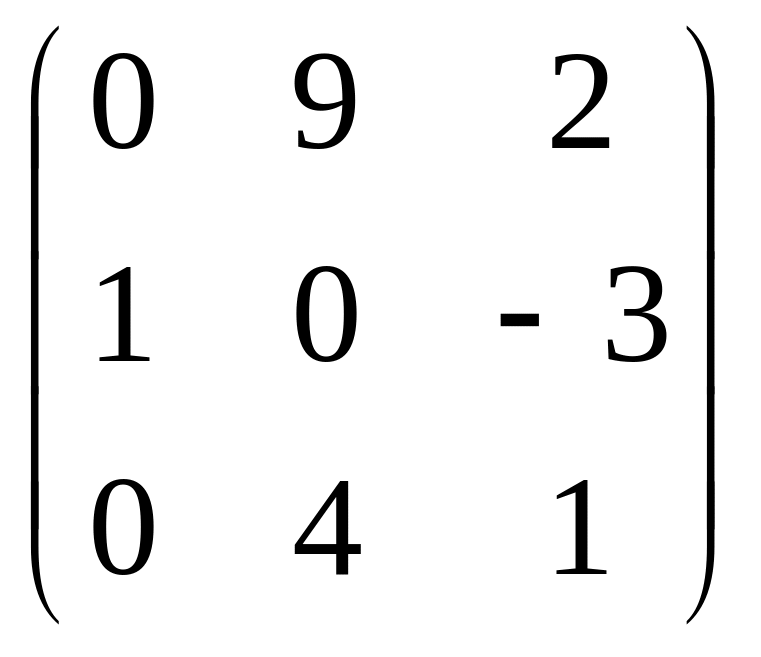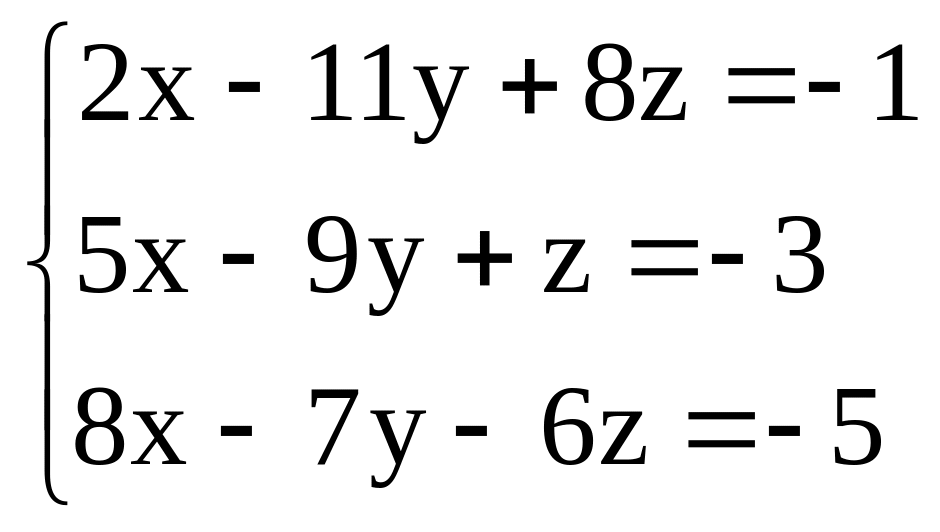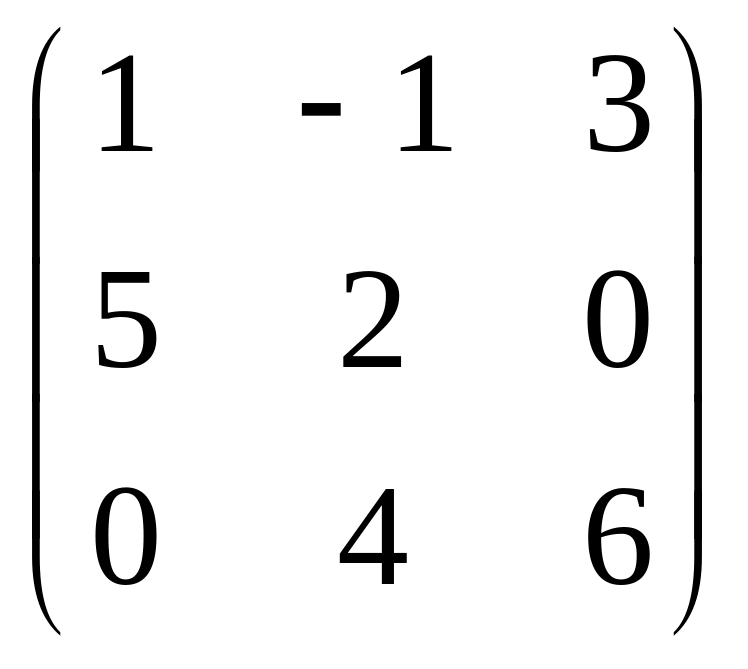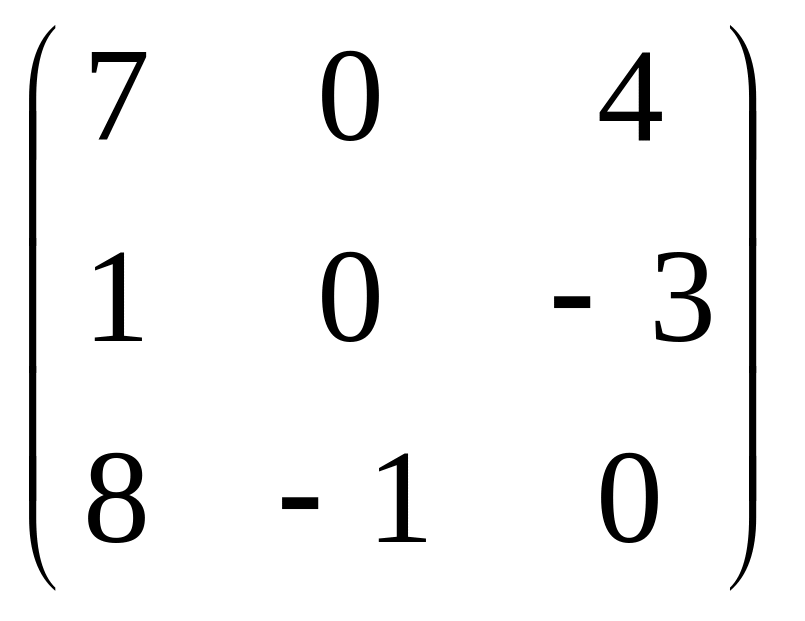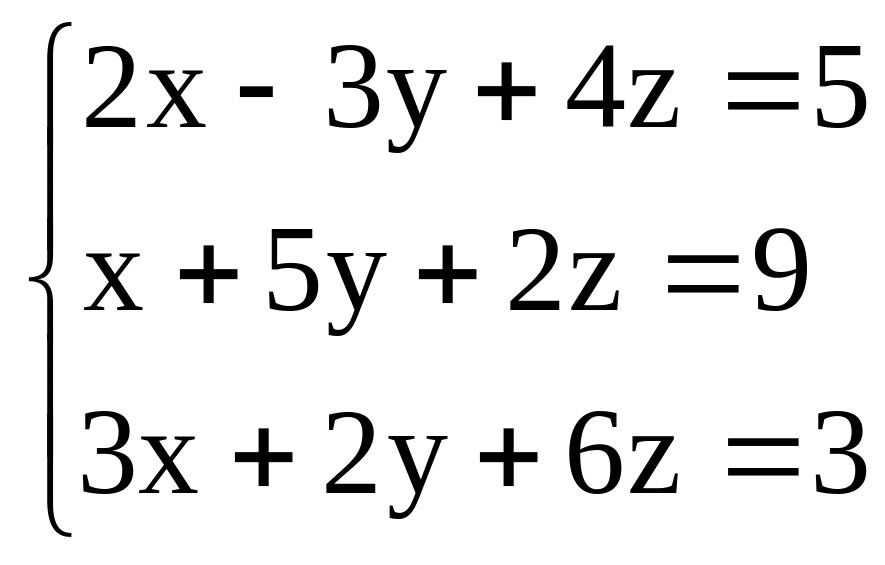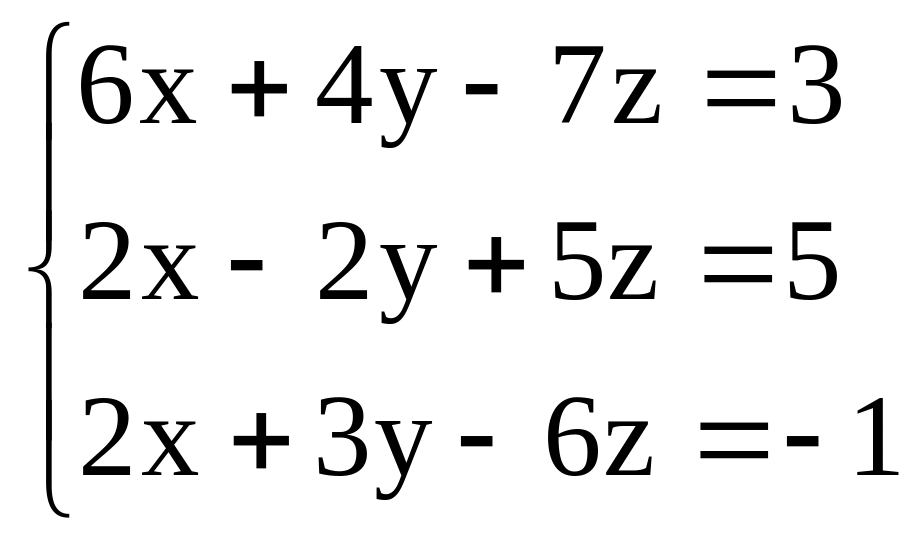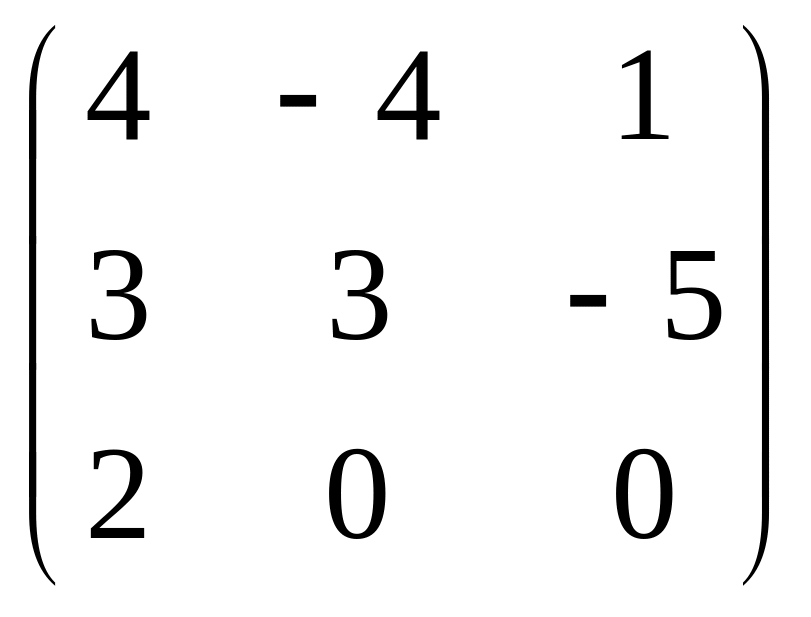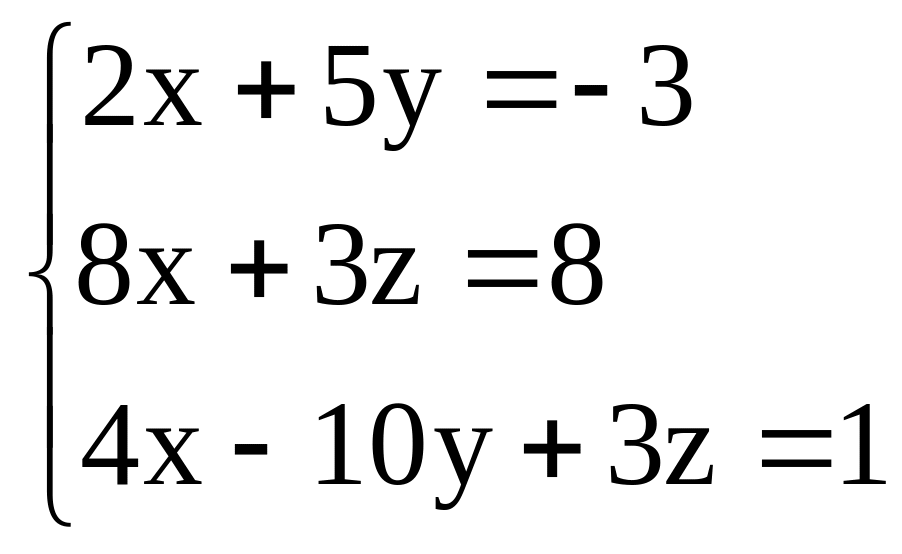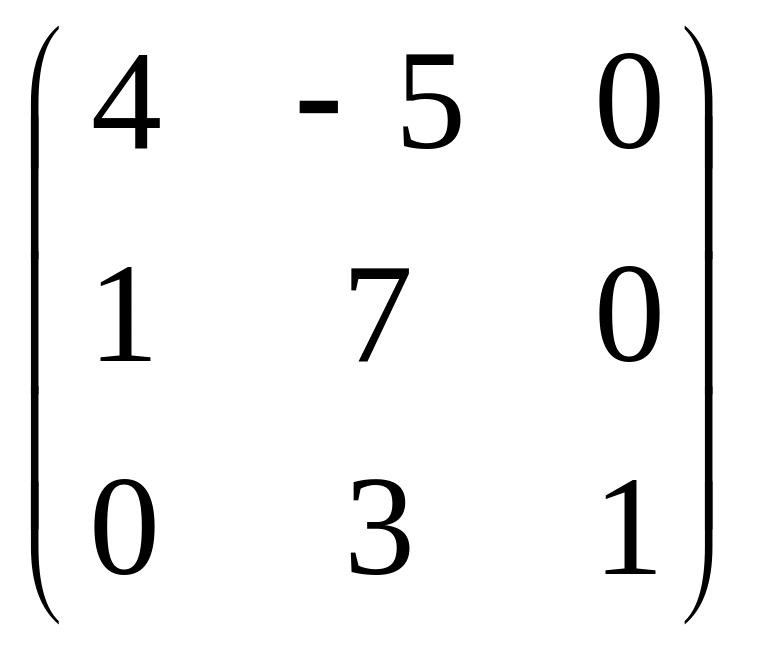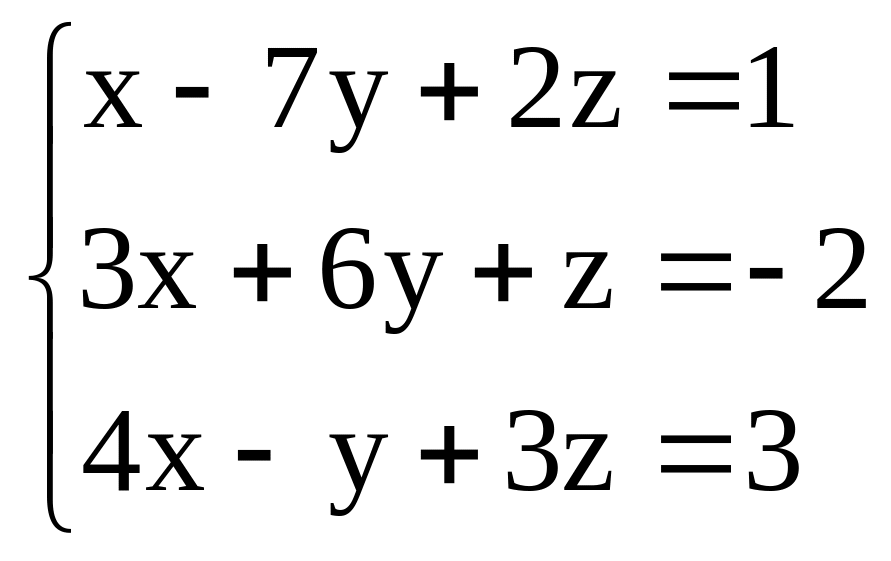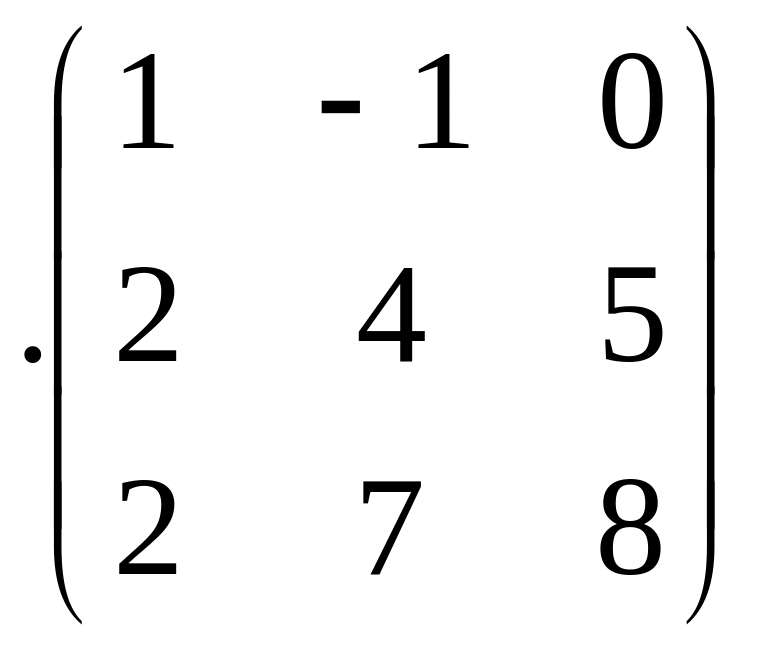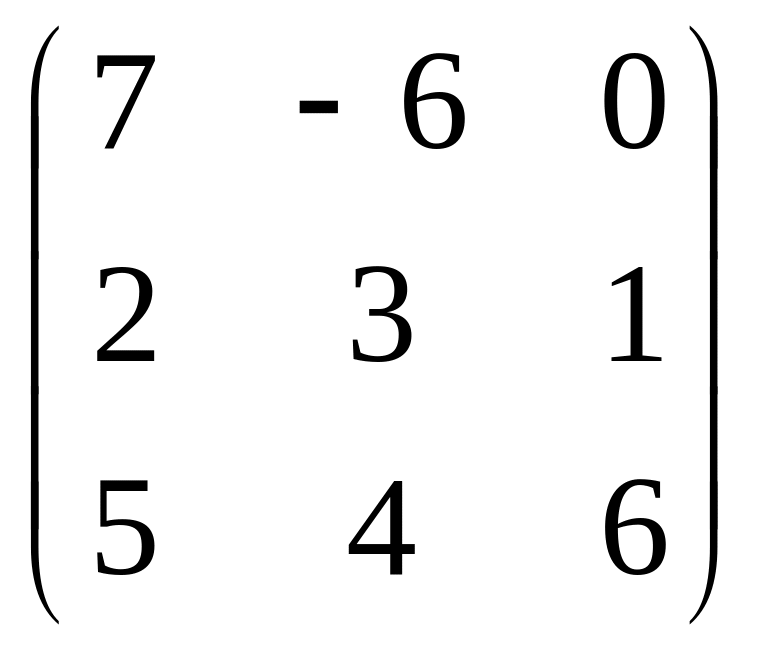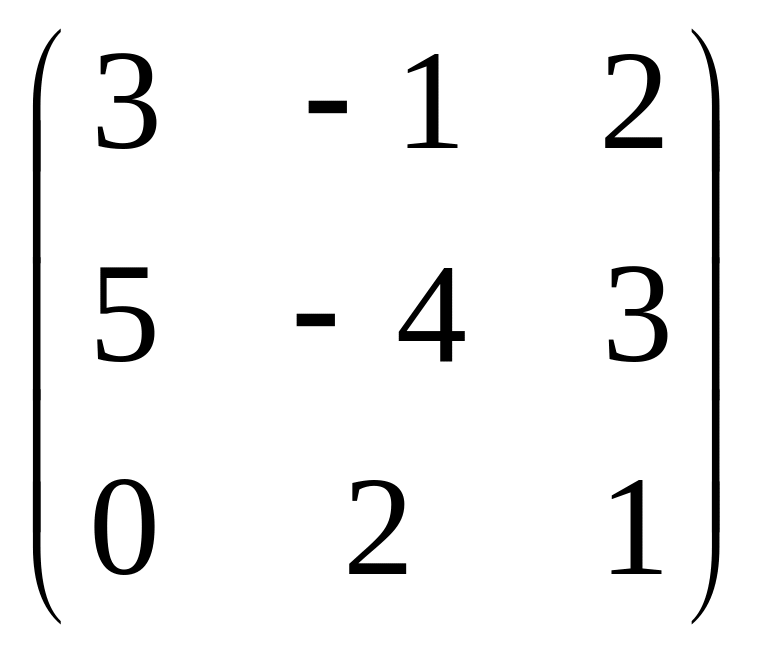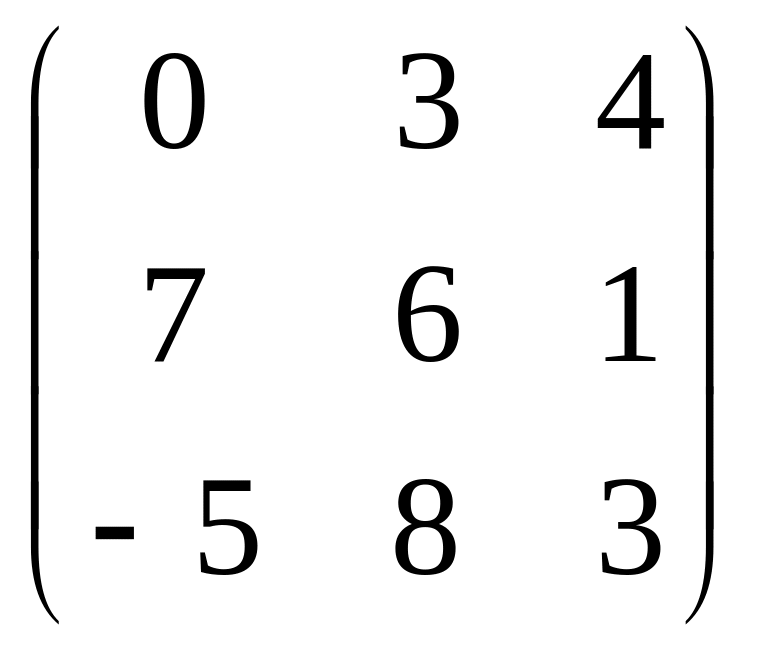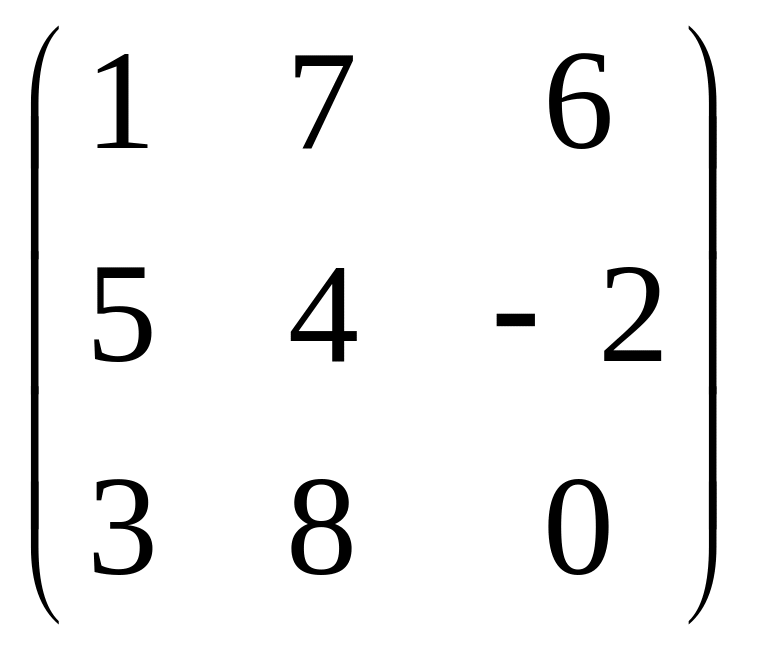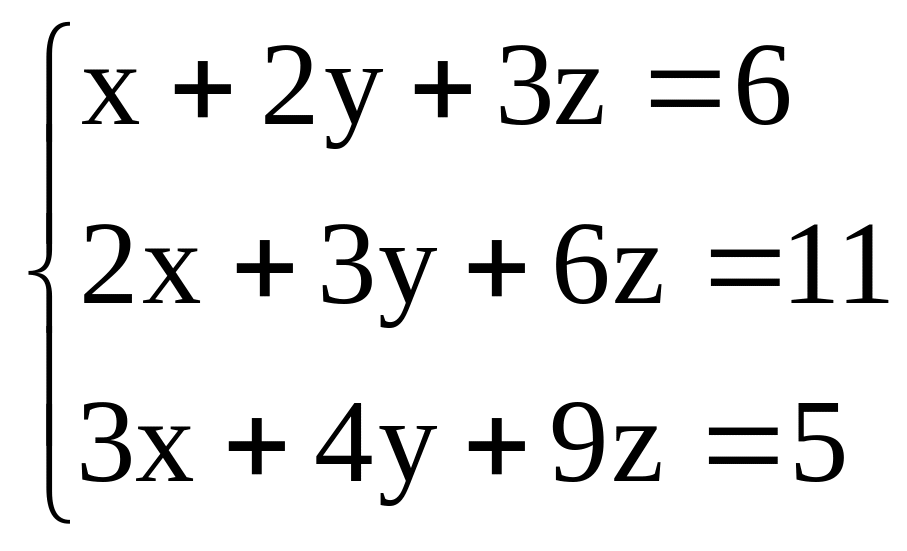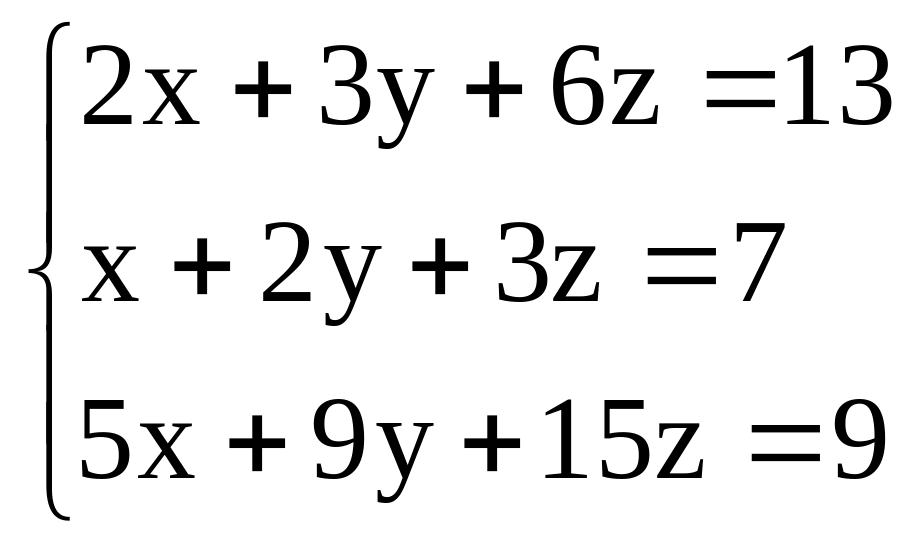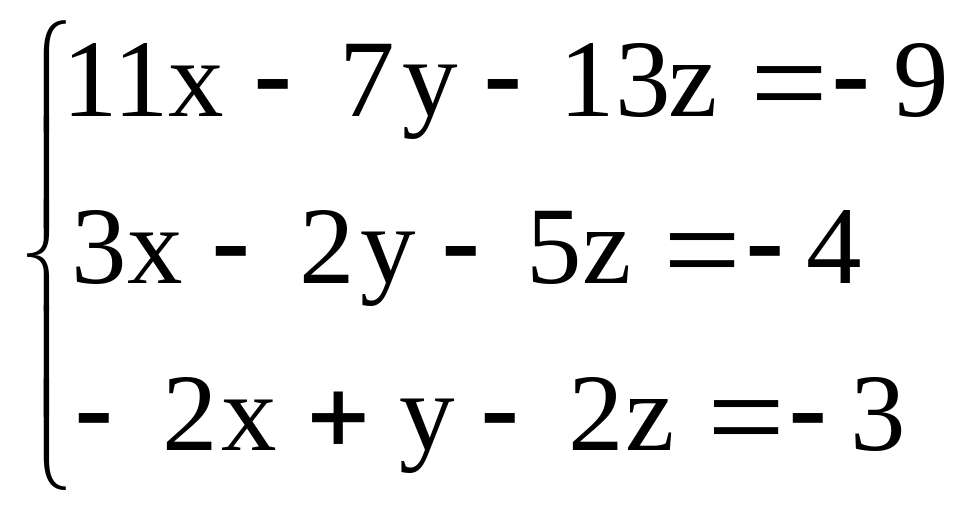Оглавление

Оглавление 3

Глава 1. Линейная алгебра и аналитическая 5

геометрия. 5

1. Определители, матрицы и системы линейных 5

уравнений. 5

2. Прямоугольные и полярные координаты на 18

плоскости. 18

3. Прямая линия. 23

4. Кривые второго порядка. 29

5. Преобразование координат и упрощение уравне- 34

ний кривых второго порядка. 34

6. Векторы. 37

7. Плоскость и прямая. 44

Глава 2. Введение в математический анализ. 55

1. Функции одной независимой переменной. 55

2. Преобразования графиков функций. 58

3. Пределы. 61

4. Сравнение бесконечно малых величин. 69

5. Непрерывность функции. 70

Глава 3. Дифференциальное исчисление 74

функций одной независимой 74

переменной. 74

1. Дифференцирование явных функций. 74

2. Производная неявно и параметрически заданных 82

функций. 82

3. Приложения производной к задачам геометрии и 85

механики. 85

4. Производные высших порядков. 87

5. Дифференциал. 90

6. Теоремы о дифференцируемых функциях. 92

7. Возрастание, убывание и экстремум функции. 96

8. Выпуклость, вогнутость и точки перегиба. 101

9. Асимптоты. 103

10. Построение графика фyнкции. 105

Глава 4. Дифференциальное исчисление функций нескольких независимых переменных. 108

1. Область определения и поверхности уровня 108

функции. 108

2. Производные и дифференциалы. 109

3. Дифференцирование сложных функций. 113

4. Производная по направлению и градиент. 116

5. Касательная плоскость и нормаль к поверхности. 118

6. Экстремум функции двух переменных. 121

Справочник по элементарной математике 125

Литература 134

Глава 1. Линейная алгебра и аналитическая

геометрия.

1. Определители, матрицы и системы линейных

уравнений.

Рассмотрим систему двух линейных уравнений с двумя неиз­вестными:

Здесь х и у – подлежащие определению неизвестные, а а_1,1, а_1,2, а_2,1, а_2,2, - заданные числа –коэффициенты системы, b₁ и b₂ – столбец правых частей. Решение такой системы проще всего ис­кать с помощью метода подстановки. Для этого из второго уравнения системы выразим неизвестное у

и подставим найденное значение в первое уравнение системы

.

Отсюда

или

Поставив найденное значение х в соответствующее выраже­ние для у, найдем

.

Заметим, что в знаменателях найденного решения стоит одно и тоже выражение = и что система имеет реше­ние в том и только том случае, когда это выражение отлично от нуля. Аналогичным образом может быть решена система линей­ных уравнений любого порядка, естественно, ценой увеличе­ния объема вычислений. Для уменьшения объема вычислений при решении систем линейных алгебраических уравнений использу­ется инструментарий определителей и матриц.

Определителем второго порядка называется число, запи-санное в виде таблицы чисел, состоящей из двух строк и двух столбцов и вычисляемое по правилу:

=a_1,1a_2,2 - a_2,1a_1,2

Подобным образом определяется понятие определителя третьего порядка:

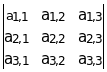=a_1,1 -a_1,2 +à_1,3

Ïîä определителем порядка n будем понимать число, записанное в виде таблицы чисел, состоящей из n строк и n столбцов. Если a_i,j - элемент определителя, стоящий на пересечении строки с номером i и столбца с номером j, то минором этого элемента М_i,j будем называть определитель порядка n-1, который получается из исходного определителя вычеркиванием из него этой строки и этого столбца. Алгебраическим дополнением элемента a_i,j называется число А_i,j =(-1)^i+j Ì_i,j Если D - определитель порядка n, то он вычисляется по правилу:

D=a_i,1À_i,1+a_i,2À_i,2 + . . . + a_i,n À_i,n , ëèáî

D=a_1,jÀ_1,j+a_2,jÀ_2,j + . . . + a_n,j À_n,j ,

где i - номер любой его строки, и j - номер любого его столбца. То есть всякий определитель равен сумме произведений элементов какой-либо своей строки (столбца) на их алгебраические дополнения.

Свойства определителей.

1. Определитель не изменится, если строки определителя заменить его столбцами, а столбцы - соответствующими строками.

2. Общий множитель элементов какой-либо строки (столбца) может быть вынесен за знак определителя.

3. Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца), то такой определитель равен нулю.

4. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.

5. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Матрицей размера nxm называется таблица чисел, содержащая n строк и m столбцов.

Квадратной называют матрицу, у которой число строк равно числу столбцов. Это число называют порядком матрицы. Если элементы квадратной матрицы удовлетворяют условию a_i,j=a_j,i (то есть элементы матрицы, симметричные относительно ее главной диагонали равны между собой), то такую матрицу называют симметрической. Транспонированной A^* к матрице А будем называть матрицу, строки которой образованы из столбцов матрицы А, а столбцы – из соответствующих строк:

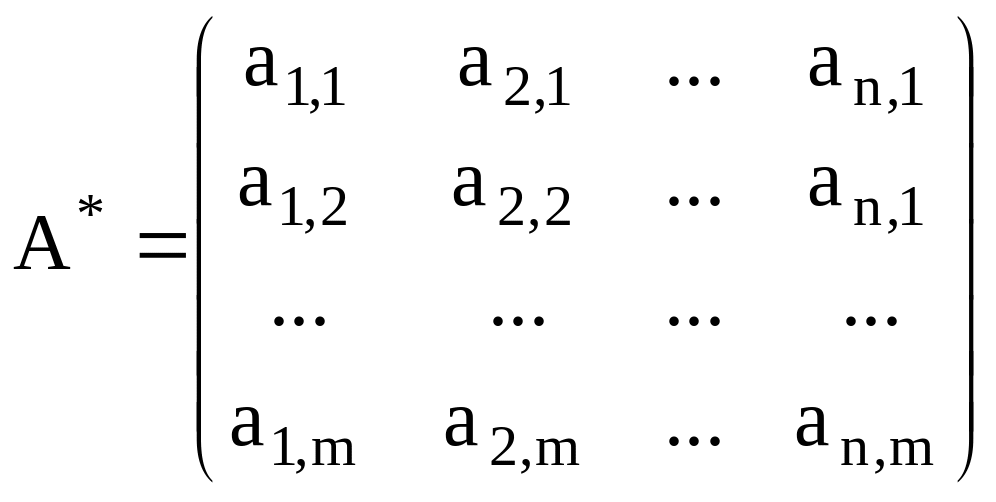
Матрицы А=(a_i,j) è Â=(b_i,j) считаются равными тогда и только тогда, когда равны их соответствующие элементы, то есть a_i,j=b_i,j . для всех i=1,…n и j=1,…m.

Операции над матрицами.

1. Умножение матрицы А=(a_i,j) на число m осуществля-ется поэлементно: mA=(ma_i,j).

2. Квадратные матрицы одного порядка складываются поэлементно: А+В=(a_i,j+â_i,j).

3. Произведением квадратных матриц А и В одного порядка называется матрица того же порядка С=АВ=(c_i,j), элементы которой определяются правилом:

c_i,j=a_i,1b_1,j+a_i,2b_2,j+ . . . +a_i,nb_n,j,

то есть элемент матрицы-произведения, стоящий в строке с номером i и столбце с номером j, равен сумме произведений соответственных элементов строки с номером i матрицы А и столбца с номером j матрицы В. Для операции произведения матриц переместительный закон не имеет места, то есть для некоторых матриц А и В может случиться так, что АВВА. Аналогичным образом определяется операция произведения прямоугольных (не обязательно квадратных) матриц. При этом, если А - матрица размера np, то ее справа можно умножить на матрицу В размера pm, при этом матрица-результат будет иметь размер mn.

Введенные операции над матрицами обладают следующими естественными свойствами:

1. A+B=B+A.

2. (A+B)+C=A+(B+C).

3. (A+B)= A+B.

4. (AB) C=A(BC).

5. A(B+C)=AB+AC.

6. (A^*)^*=A.

7. (A+B)^*=A^*+ B^*.

8. (AB)^*= B^*A^*.

С каждой квадратной матрицей А=(a_i,j) связан ее определитель D_A=detA=a_i,j. Матрица А называется невы-рожденной, если ее определитель отличен от нуля. В про-тивном случае матрицу называют вырожденной или особой. Единичной E=(å_i,j) называют матрицу, все элементы которой, стоящие на главной диагонали, равны единице, а все остальные равны нулю, то есть e_i,i=1 äëÿ âñåõ i=1,..n è e_i,j=0, если ij. При умножении единичной матрицы слева или справа на произвольную матрицу исходная матрица не изменяется: ЕА=АЕ=А. Матрица В называется обратной к матрице А, если АВ=ВА=Е. Для матрицы, обратной к матрице А принято обозначение A^-1_.

Всякая невырожденная квадратная матрица А имеет обрат-ную, которая может быть вычислена так

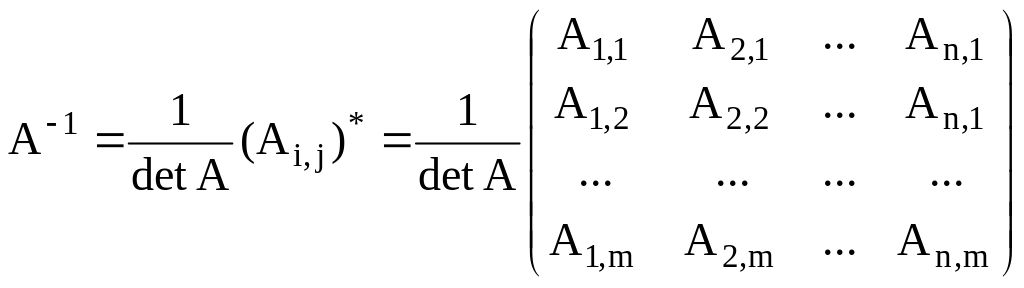
Зäåñü À_i,j- алгебраическое дополнение элемента a_i,j в опре-делителе detA.

Решение системы линейных уравнений

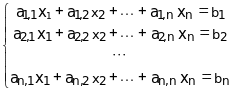
определитель которой

D =

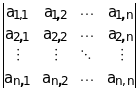
отличен от нуля, определяется по формулам Крамера

x₁₌ , x₂= , . . . , x_n= ,

ãäå D_k - определитель, который получается из определителя системы D заменой в нем столбца с номером k столбцом правых частей системы.

В соответствии с правилом перемножения матриц всякая система линейных уравнений может быть записана в матричном виде

ÀÕ=Â, ãäå

A=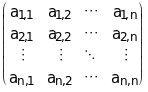 , Õ= , B=(b₁, b₂ ,. . ., b_n).

Решение этой системы имеет вид Х=А^-1В, если конечно матрица А системы является невырожденной, что соответствует ситуации, когда ее определитель, то есть опре-делитель системы D, отличен от нуля.

Если же определитель системы D равен нулю, то такая система либо неопределенна, либо несовместна, то есть либо имеет бесчисленное множество решений, либо решений не имеет вообще.

Пример 1. Вычислить определитель третьего порядка

Решение. Разложив определитель по элементам 1-й строки, получим

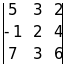=5 -3 +2 =

=5(26-34)-3(-16-74)+2(-13-72)=

=50-3(-34)+2(-17)=68.

Тот же результат можно получить манипулируя со строками исходного определителя. Именно, к элементам первой строки прибавим соответствующие элементы второй, умноженные на 5, а к элементам третьей - соответствующие элементы второй, умноженные на 7:

=

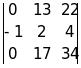
Разложив последний определитель по элементам первого столбца, получаем:

=0 +1 +0 =

=1334-1722=68.

Пример 2. Найти А² , åñëè A= .

Решение.

A²= = .

Пример 3. Найти обратную А^-1 к матрице

A= .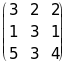

Решение. Вычислим определитель матрицы А:

D_A= =3 -2 +2 =27+2-24=5.

Теперь найдем алгебраические дополнения элементов этого определителя:

A_1,1= =9, A_2,1=- =-2, A_3,1 = =-4,

A_1,2=- = 1, A_2,2= =2, A_3,2=- =-1,

A_1,3= =-12, A_2,3=- =1, A_3,3=- =7.

Следовательно,

A^-1= .

Пример 4. Решить систему линейных уравнений:

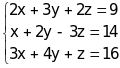
Решение. Вычислим определитель D этой системы и определители D_x, Dy, Dz, связанные с неизвестными:

D = =214-310+2(-2)=-6.

D_x=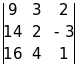 =914-362+224=-12,

D_y=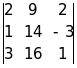 =268-910+2(-26)=-18,

Dz=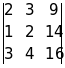 =2(-24)-3(-26)+9(-2)=12.

Тогда по формулам Крамера

x=D_x/D =2, y=Dy/D=3, z=Dz/D=-2.

Тот же результат можно получить другим способом. Представим нашу систему в матричном виде AX=B, где

A= , X= , B=(9,14,16).

Решение этого матричного уравнения имеет вид X=A^-1B, поэтому найдем матрицу A^-1, обратную к матрице A. Для этого вычислим определитель этой матрицы D_A=D=-6 и алгебраические дополнения элементов этого определителя

A_1,1= = 14, A_2,1=- =5, A_3,1= =-13,

A_1,2= =-10, A_2,2=- =-4, A_3,2= =8,

A_1,3= =-2, A_2,3= - =1, A_3,3= =1.

Таким образом,

A^-1=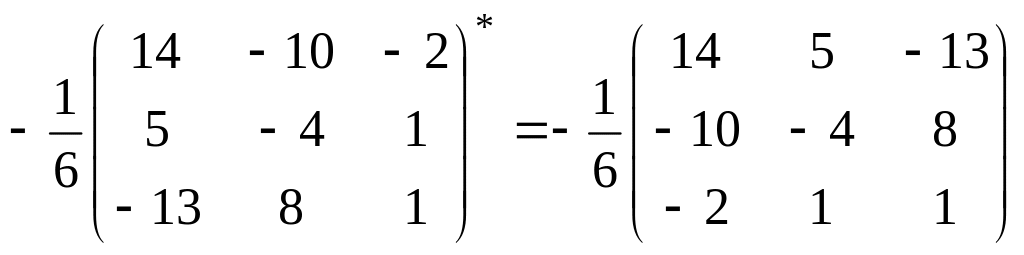

откуда

X= A^-1B= = =

= = .

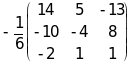
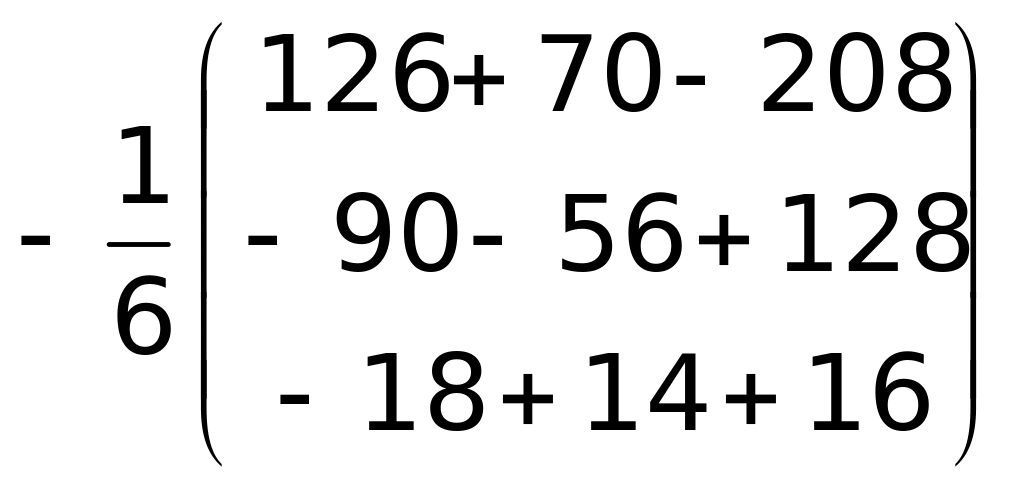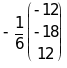Следовательно, x=2, y=3, z=-2.

Решение системы линейных уравнений может быть най-дено с помощью метода Гаусса. Суть этого метода состоит в последовательном исключении неизвестных из системы.

Пример 5. Методом Гаусса найти решение системы линейных уравнений

.

Решение. Второе уравнение системы заменим разностью его самого и первого уравнения, помноженного на 2. Аналогично, третье уравнение системы заменим разностью его самого и второго уравнения, помноженного на 3:

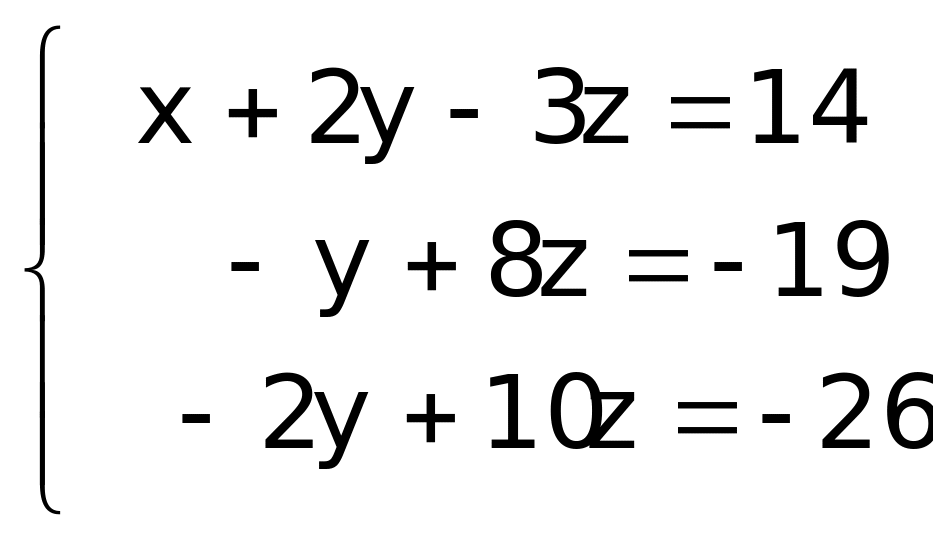
Теперь третье уравнение системы заменим разностью его самого и второго уравнения, помноженного на 2:

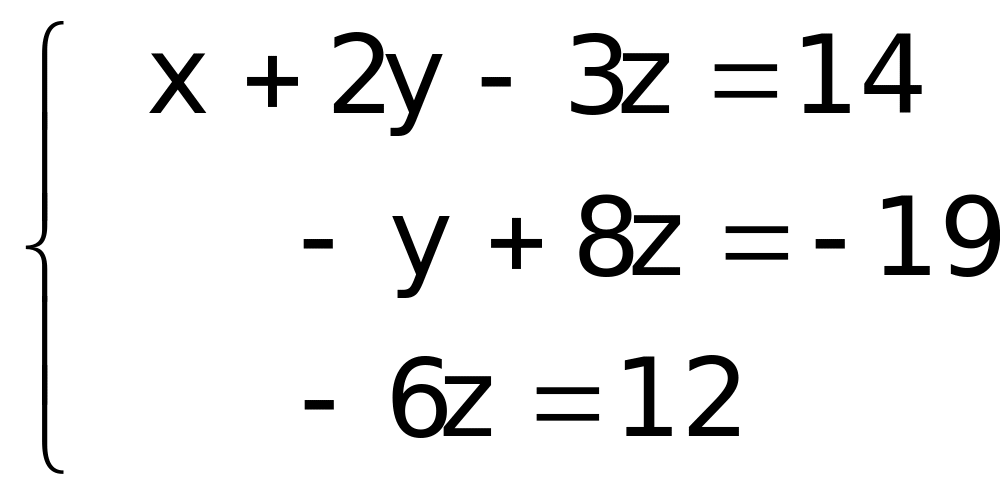
Из третьего уравнения находим z=-2 и, подставив это значение во второе уравнение системы, находим y=3, и, наконец, подставив найденные значения у и z в первое уравнение, находим x=2.

Задача 1. Даны матрицы А и В. Требуется

1. Вычислить матрицу С=3А+2В²-5AÂ+8Å.

2. Найти значение многочлена f(A) от

матрицы А, если f(x)=3x²-2x+5.

3. Решить матричные уравнения АХ=В,

ÕÀ=Â.

Задача 2. Доказать совместность и найти решение системы линейных уравнений по правилу Крамера и средствами матричного исчисления.

Задача 3. Методом Гаусса найти решение системы линейных уравнений

N	Задача 1 матрица A	Задача 1 матрица В	Задача 2	Задача 3
1
2
3
4
5
6
7
8
9
10