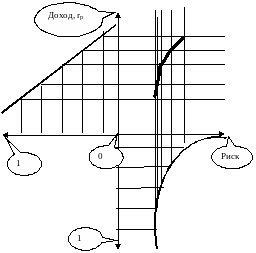
E. Соединение графиков доходности и риска для инвестиционного портфеля с двумя видами ценных бумаг

Из предыдущих форм связи доходности и риска портфеля из двух ценных бумаг с долями ценных бумаг, можно вывести зависимость между доходом и риском.

_{Рис. 8. Связь риска (дисперсии) и доходности для портфеля из двух ценных бумаг}

Если мы имеем три ценные бумаги S, Q, J, то риск и доходность инвестиционного портфеля (при известных риске и доходности каждой ценной бумаги) принимает следующий вид

_{Рис. 9. Связь риска (дисперсии) и структуры для портфеля из трех ценных бумаг}

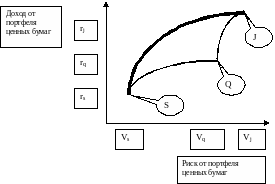
Обратим внимание на существование множества допустимых портфелей, которое определяется точками по границам и внутри криволинейного треугольника. Но легко видеть, что инвестор, ищущий наибольшей доходности при допустимом риске или наименьшего риска при желаемой доходности, выйдет на крайнюю левую границу, которую и называют эффективной границей.

Приведем схему аналитического вывода взаимозависимости риска и доходности для портфеля из двух ценных бумаг.¹²

Пусть:

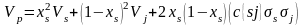
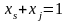
Тогда из уравнения для доходности находим, что:

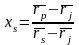
Это значение подставляем во второе уравнение (уравнение риска портфеля) и т. д. и получаем соответствующее квадратное уравнение:

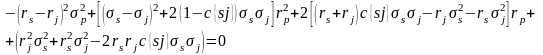Квадратное уравнение может быть исследовано по знаку определителя матрицы, составленной из коэффициентов при членах второго порядка:

Вывод:

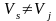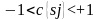При и кривая является гиперболой.

При и кривая является парой прямых.

При и 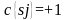кривая является прямой.

Для понимания конфигурации допустимого множества решений, рассмотрим крайние случаи:

1. Положим, что коэффициент корреляции двух ценных бумаг равен +1.

Тогда, учитывая, что

можно представить как

,

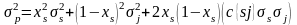Получаем при :

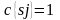или

.

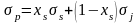Итак, мы получили отрезок, параметрически заданный на двумерной плоскости 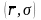следующими уравнениями:

.

2. Положим, что коэффициент корреляции двух ценных бумаг равен (-1). Тогда аналогичным образом приходим к следующим уравнениям:

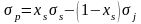
Положим . Тогда

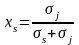и

И при 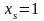имеем

В конце концов, мы получаем следующую конфигурацию допустимого множества для двух ценных бумаг при изменении коэффициента корреляции от (-1) до (+1).

Рис. 10. Допустимое множество для портфеля из двух ценных бумаг

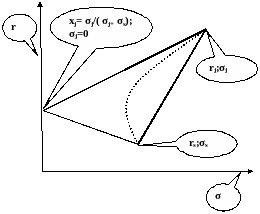
F. Эффективные инвестиционные портфели

Учитывая уровень минимальной желаемой доходности и максимального терпимого риска, портфель может быть выбран из долей по эффективной границе криволинейного треугольника.

Точное определение оптимальной точки (участка) на кривой дохода и риска может быть получено путем решения оптимизационной задачи, которая позволяет найти касательную к эффективной кривой дохода и риска.¹³

Аналитическое решение основывается на доказательстве существования и единственности оптимума выпуклой функции полезности, определенной на выпуклом эффективном множестве решений, на границе допустимого множества.

Подход Г. Марковица заключается следующем¹⁴. Пусть имеется видов акций. Инвестор хочет распределить средства между акциями таким образом, чтобы, например, при заданном уровне желаемого дохода собрать портфель из различных акций с минимальным уровнем риска (минимальным среднеквадратическим отклонением портфеля бумаг).

Аналитическая формулировка задачи Г. Марковица:

Найти , такие, что

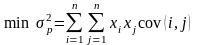
При условиях:

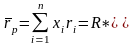
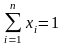, где

- доли вложения средств в ценные бумаги, ;

- ожидаемая средняя доходность портфеля ценных бумаг;

- ожидаемая средняя доходность -й ценной бумаги;

- среднеквадратическое отклонение доходности портфеля ценных бумаг;

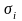- среднеквадратическое отклонение доходности -й ценной бумаги;

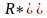- желаемая величина доходности портфеля ценных бумаг.

Если некоторые окажутся меньше 0, это означает, что инвестору следует осуществить «короткую» продажу этих ценных бумаг.

Рис. 11. Графическое решение задачи и обоснование выбора.¹⁵

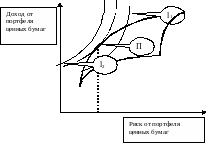
Предположим, что существует точка 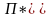касания кривой безразличия инвестора и эффективного множества портфелей. Тогда оптимальный портфель находится в точке .

Обоснование.

Рассмотрим произвольную линию уровня 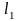, пересекающую эффективное множество портфелей. Оптимальный портфель на этой линии не лежит. Почему? Потому что существуют допустимые портфели, лежащие левее и выше линии .

Рассмотрим линию уровн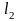я . Значение функции полезности на линии уровня больше, чем на рассмотренной ранее линии . Однако оптимальный портфель и на ней не лежит. Почему? Потому что на этой линии , вообще, не лежит ни одного портфеля.

Следовательно, оптимальный портфель лежит правее и ниже линии .

Оптимальный портфель лежит между линиями и . Оптимальный портфель лежит на линии проходящей через точку .