Приложение к модели г. Марковица a. Вывод функции полезности и формулы риска для портфеля
1. Вывод квадратной функции полезности, включающей непосредственное измерение риска39
Полезность любого дохода инвестиционного портфеля может быть найдена путем подстановки этого дохода в общую формулу квадратной функции полезности. В результате получим:
,
где
-
общая полезность
-го
дохода (
)
портфеля.
Ожидаемая полезность портфеля может быть найдена из расчета средневзвешенной полезности, получаемой от каждого возможного дохода с использованием в качестве весов вероятностей этих доходов.
,
где
- ожидаемая полезность портфеля.
Выполнив умножение в последнем выражении, получим:
.
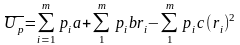Первый
член в правой части равен
,
так как сумма вероятностей всех возможных
доходов равна 1.
Второй
член в правой части представляет собой
ожидаемый доход портфеля, умноженный
на
.
Значение третьего члена в правой части уравнения не очевидно.
Запишем
каждый входящий в третий член доход в
виде суммы ожидаемого дохода портфеля
и разницы между ним и отдельно
рассматриваемым доходом, то есть каждый
может быть выражен как
.
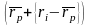Используя такие обозначения, третий член может быть записан в виде:
.
Перемножив выражение в скобках, получим:
Первый
член этого выражения после умножения
становится равным
.
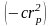Можно также показать, что последний член равен нулю.
Второй
элемент после умножения на
будет
представлять дисперсию дохода портфеля.
Таким образом, последнее выражение может быть переписано:
.
Наконец, выражение ожидаемой полезности портфеля может быть представлено следующим образом:
.
2. Вывод формулы риска инвестиционного портфеля для ценных бумаг двух типов
Основное определение дисперсии распределения вероятностей случайной переменной ( ) имеет вид:
.
где
а) - один из возможных доходов от - й ценной бумаги:
,
где - прогноз будущей стоимости ценной бумаги в конце определенного периода плюс дивиденды;
- размер первоначальной инвестиции.
б)
- математическое ожидание дохода от
-
й ценной бумаги
,
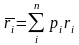где - вероятность - го дохода от - й ценной бумаги
в)
- дисперсия дохода от
-
й ценной бумаги
Поэтому дисперсия портфеля ( ) может быть записана так:
,
где
-
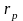один из возможных доходов от портфеля
ценных бумаг
Если портфель состоит из двух ценных бумаг ( и ), а весами являются доли и в портфеле ( и ), тогда
.
Путем простых преобразований приходим к:
,
где
-
ковариация двух случайных величин,
доходов
и
от
двух ценных бумаг
и
.
3. Алгебраическое решение для риска портфеля, содержащего ценные бумаги двух видов
Напомним, что риск портфеля для ценных бумаг двух видов определяется так
или
,
где
- коэффициент корреляции двух ценных бумаг
- квадратические отклонения в распределении двух ценных бумаг
Учитывая, что , можно написать:
А) Если коэффициент корреляции равен 1, то есть, в случае линейной положительной корреляции двух ценных бумаг, выражение для дисперсии портфеля примет вид:
Или
В этом случае дисперсия портфеля, а значит, риск, становятся максимальными.
Б) Если корреляция между двумя ценными бумагами уменьшается до 0, дисперсия становится следующей:
В) Дисперсия (риск) минимальны, когда корреляция двух ценных бумаг равна (-1):
или
Напомним из теории вероятности анализ дисперсии суммы случайных величин
Заменим
третий элемент, учитывая что
,
и дисперсию суммы двух случайных величин
представим следующим образом:
Итак:
,
где
-
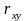корреляция между случайными величинами
и
-
квадратические отклонения случайных
величин
и
Как мы видим, уже дисперсия суммы двух величин несет на себе результат их взаимовлияния. Положительная корреляция увеличивает дисперсию суммы, отрицательная уменьшает.
Дадим графическое представление суммирование двух случайных величин. Рассмотрим варианты совмещения случайных величин, изменяющихся согласовано.
Первый вариант – случайные величины почти функционально связаны и согласовано изменяются в одном направлении. Суммирование таких случайных величин дает случайную величину с дисперсией почти равной сумме дисперсий слагаемых.
Случайная величина (А+В)
Второй вариант – случайные величины тоже связаны почти функционально, но меняются почти строго в обратном направлении. Суммирование таких случайных величин дает случайную величину с почти нулевой дисперсией. Последний пример показывает возможность снижения рисков при формировании портфелей из бумаг с обратным движением доходности.
Однако, приведенная формула не учитывает различия в структуре «портфеля случайных величин». Если ввести показатели структуры портфеля, а именно доли двух ценных бумаг в портфеле ( и ), мы получим формулу: