4. Ротор. Теорема Стокса

4.1. Ротор. В 1.2 было показано, что для полей потенциальных циркуляция при однозначности потенциала равна нулю (п. 4). Однако в общем случае циркуляция вектора по некоторому контуру L не должна обязательно быть равной нулю. Подобно потоку вектора, циркуляция также может быть использована для локальной характеристики поля. При этом возникает понятие ротора вектора , обозначаемого символом rot . По определению, rot есть вектор, проекция которого на произвольное направление выражается следующим образом:

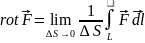(4.1)

где ΔS - площадка, выбранная так, что есть нормаль к ней, a L - контур этой площадки, направление обхода которого при интегрировании составляет с нормалью правовинтовую систему (если смотреть вдоль нормали, то обход производится по часовой стрелке).

4.2. Ротор в декартовых координатах. Как и дивергенцию, ротор вектора нетрудно представить в виде дифференциального выражения в декартовой системе координат. Обратимся к рис. 4.1, на котором через произвольную точку М(х, у, z) проведены три координатные линии и построены элементарные площадки, лежащие в координатных плоскостях. Желая сначала найти проекцию вектора на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)

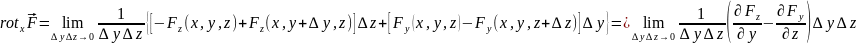
Таким образом,

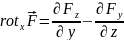(4.2a)

Совершенно аналогично получаем:

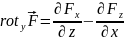, (4.2б)

и

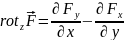. (4.2в)

Эти три равенства удобно объединяются в форме определителя:

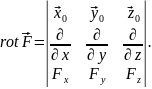(4.3)

Нетрудно показать, что потенциальные поля являются обязательно «безвихревыми», т. е. для всякого вектора будет 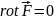. Чтобы проверить тождество

, (4.4)

достаточно рассмотреть какую-либо одну его проекцию. Так, составляя по формулам (4.2а) и (2.4а) проекцию этого вектора на ось х, имеем:

.

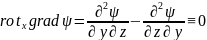Другой важный факт заключается в том, что дивергенция вихревого поля тождественно равна нулю, т. е. такое векторное поле соленоидально (3.2):

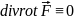. (4.5)

Действительно,

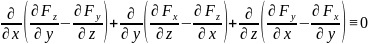
Из определения ротора, его можно трактовать в физическом смысле как вихрь.

4.3. Теорема Стокса. Перейдем, наконец, к теореме Стокса, содержание которой выражается равенством:

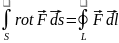, (4.6)

где S - некоторая поверхность, a L - её контур, направление обхода которого при интегрировании согласовано с направлением положительной нормали к S, как и ранее. Согласно теореме Стокса, поток ротора некоторого вектора F через поверхность S равен циркуляции самого вектора по соответствующему контуру L.

Чтобы убедиться в справедливости теоремы Стокса, разобьем произвольную поверхность S на достаточно малые элементарные площадки Δs_i (рис. 4.3) и для определения ротора внутри Δs_i воспользуемся приближённым соотношением

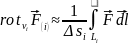
есть внутри Δs_i) вместо (4.1). Поскольку точность этого равенства может быть как угодно велика (достаточно лишь взять соответственно малые размеры элемента Δs_i), то

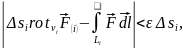
где ε – наперёд заданная сколь угодно малая положительная величина.

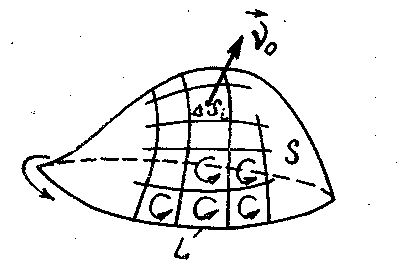
Рис. 4.3

Выбрав все элементы достаточно малыми, произведём суммирование по i и получим:

где фигурирует циркуляция по граничному контуру L всей поверхности S, поскольку при суммировании части циркуляции по общим границам смежных элементов 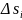взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.

Неограниченно измельчая все элементы и переходя соответственно этому от суммы к интегралу (N→∞), а также учитывая произвольную малость ε, приходим от предыдущего равенства к формулировке теоремы Стокса (4.6).