19. Ортогональные системы функций и ряды Фурье

19.1. Некоторые свойства оператора Лапласа. Рассмотренные выше граничные задачи (18.1) и (18.11), а также задачи (18.41), (18,42) и ряд других можно кратко сформулировать в виде

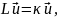(19.1)

где 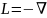² - взятый с обратным знаком оператор Лапласа, параметр к - это k² или χ ² (в. зависимости от того, является ли задача трёхмерной или двумерной), а 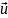– векторные или скалярные ( = и) функции, подчинённые требуемым граничным условиям. Обычно граничные условия задаются вместе с оператором L; они определяют класс функций и, на которые может распространяться действие L, т. е. область определения оператора D_L. Разумеется, функции , принадлежащие этому классу (кратко пишут: 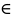D_l ), должны допускать заданные операции дифференцирования. Говорят, что запись (19.1) выражает общую формулировку задачи на собственные значения оператора L. В частности если и = 0 на S для D_l, получаем задачу (18.1), если и_τ = 0 и div = 0 на S для D_l - задачу (18.41), и т. д.

Введём интегральную величину, имеющую своё обозначение:

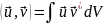(19.2)

Здесь подразумевается область V трёхмерной задачи, а в случае задачи двумерной интегрирование производится по её области S; величина 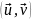называется скалярным произведением функций 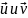, последние могут быть как векторами, так и скалярами. Заметим, что (v, и) = (и, v) *.

Оператор L, обладающий тем свойством, что для

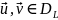
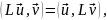(19.3)

является по определению симметрическим. Легко убедиться, что для всех поставленных в п.18 задач оператор ² симметрический.

Действительно, в случае скалярных uиv на основании первой формулы Грина (5.13)

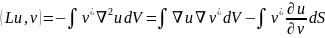(19.4)

Как для первой граничной задачи (18.1) (и = 0, v = 0 на S), так и для второй задачи (18.11) 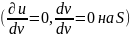поверхностный интеграл в (19.4) равен нулю. Меняя местами u и v*, мы оставляем правую часть (19.4) неизменной, а потому

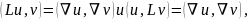(19.4а)

т. е. равенство (19.3) выполняется.

Взяв векторные , получаем:

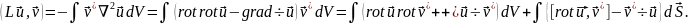(19.5)

(были использованы формулы векторного анализа (5.12), (5.10), (5.9) и (3.8)).

Если функции подчинены граничным условиям задачи (18.41) (u_τ = 0, div = 0 и v_τ = 0, div = 0 на S) или граничным условиям задачи (18.42) (u_τ = 0, (rot )_τ = 0 и v_τ = 0, (rot )_τ = 0 на S), то поверхностные интегралы в (19.5) равны нулю, и правая часть остается неизменной при замене 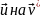и обратно. Поэтому

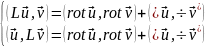, (19.5a)

и выполняется равенство (19.3).

Установленное свойство (19.3) сохраняется и для двумерных областей, т. е. при замене V на S, а граничной поверхности S объема V на контур L поверхности S. Читателю рекомендуется проверить это в качестве упражнения.

Нетрудно убедиться, что собственные значения задачи (19.1) при симметрическом операторе ² вещественны и неотрицательны. Образуя в (19.1) слева и справа скалярные произведения с , имеем:

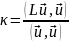(19.6)

Знаменатель 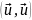положителен. В силу (19.3) 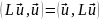, и в то же время 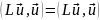*. Отсюда следует, что числитель - величина вещественная. Следовательно, вещественны и собственные значения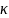

Рассматривая отдельно скалярные и векторные задачи, числитель в (19.6) преобразуем при помощи соотношений (19.4а) и (19.5а). Мы видим, что

(19.7)

и

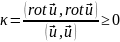(19 8)

Итак, собственные значения κ = κ_i задачи (19.1) неотрицательны и могут быть расположены в следующем порядке:

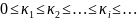(19.9)

19.2. Ортогональные системы функций. Две функции и и v называются oртогональными, если их скалярное произведение равно нулю:

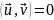. (19.10)

Пусть 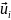(i = 1, 2, ...) - собственные функции задачи (19.1), которым соответствуют собственные значения κ; предположим, что все κ_i различны, или, как говорят, отсутствует вырождение. Взяв две любые собственные функции 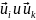, перепишем формулировку (19.1):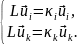

Образуя скалярные произведения (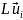 , 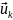) и (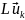 , ) и принимая во внимание вещественность собственных значений, получаем:

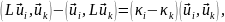
или, в силу симметричности L

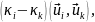= 0, (19.11)

а отсюда следует, что 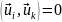, т. е собственные функции и_i ортогональны.

Задача на собственные значения (19.1) порождает, таким образом, ортогональные системы функций .

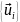Ортогональная система всегда может быть нормирована, т. е. можно так подобрать постоянные коэффициенты в выражениях , что 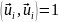для всех i. Тогда получается ортонормированная система, для которой

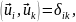(19.12)

где δ_ik= 0 при i ≠ к и δ_ik = 1 при i = k (символ Кронекера). Путём проверки нетрудно убедиться, что различные собственные функции, полученные в п.18, образуют ортогональные системы. Возьмём, например, систему функций и^тпр (18.14):

.

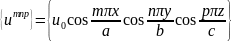Скалярное произведение двух функций и^тпр и 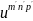имеет вид:

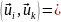
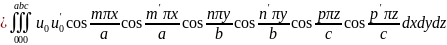
(i и k надо понимать как совокупность чисел т, п, р и т', п', р' соответственно). Поскольку

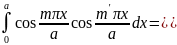
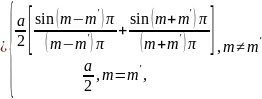
и таковы же интегралы по у и z, то, как видно, скалярное произведение действительно обращается в нуль при i ≠ k (т. е. т ≠ т', п ≠ п' и р ≠ р'). Отсюда же следует, что система 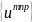будет ортонормированной, если взять

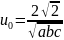
при т ≠ 0, п ≠ 0, р ≠ 0. Когда среди чисел т, п и р имеются нули, и₀ столько раз делится на 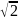, каково число нулей (один, два или три).

Предлагаю при помощи формул (16.24) и (16.26) проверить ортогональность и ввести нормировку функций и^пт (18.29). При этом следует отдельно рассматривать функции с С ≠ 0, D = 0 и С = 0, D ≠ 0 (либо Q ≠ 0, Т = 0 и Q = 0,T ≠ 0).

19.3. Ортогональные ряды. Взяв ортонормированную систему функций 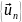и некоторую функцию 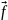, определённую в той же области, построим ряд

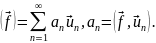(19.13)

Он называется ортогональным рядом, или рядом Фурье функции , а а_п - коэффициентами Фурье.

Отличительным свойством ряда Фурье 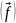является выполнение равенства

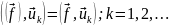(19.14)

Действительно, составляя в (19.13) скалярное произведение с , справа получаем нуль во всех членах кроме k-го, который дает а_k; равенство (19.13) превращается в выражение коэффициента Фурье а_k.

Говорят, что ряд Фурье сходится в среднем к , а система {и_п} полна (в этом смысле), если

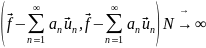0 (19.15)

Системы собственных функций оператора Лапласа обладают указанным свойством полноты при всевозможных функциях которые приходится рассматривать практически (например, с разрывами второго рода).

Легко убедиться, что обычные тригонометрические ряды Фурье дают частный пример ряда (19.13).

Возьмём, например, систему собственных функций одномерного оператора Лапласа из п.7.2. После нормировки в (7.9) 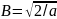, и система принимает вид:

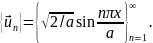
По этой системе разложим некоторую функцию f(x), определённую на отрезке 0 ≤ х ≤ а. Согласно (19.13)

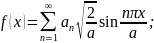
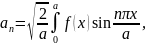а это и есть обычный тригонометрический ряд Фурье по синусам.

В качестве второго примера рассмотрим ряд Фурье типа (12.22). В данном случае разлагается определённая на отрезке –T/2 ≤ t ≤ T/2 функция 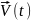, по ортонормированной системе

Ряд (19.13) имеет вид

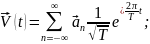
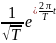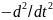что совпадает с (12.22), (12.23). Заметим, что - это собственные функции одномерного оператора Лапласа при периодических граничных условиях и (-Т/2) = и(Т/2).