21. Проекционные методы

21.1. Исходные представления. Метод Галёркина. Вернемся к рядам Фурье (п.19.3), чтобы провести следующее сравнение.

Пусть в трехмерном пространстве выбрана декартова система координат и, следовательно, имеются три единичных взаимно перпендикулярных вектора:

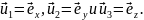
Взяв произвольный вектор 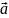, мы можем разложить его по этим ортам (рис. 21.1),что даёт:

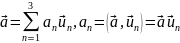(21.1)

Вектор теперь представлен при помощи трёх своих проекций 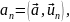являющихся скалярными произведениями на единичные базисные векторы .

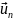Сопоставляя (21.1) и (19.13), замечаем отчётливую формальную аналогию между построенным разложением обычного вектора и рядом Фурье функции 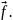Функция подобна вектору в бесконечномерном пространстве, а её ряд Фурье можно рассматривать как разложение этого вектора в базисе, образованном ортонормированной системой .

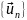Далее, пусть поставлена задача (быть может, некоторая граничная задача электродинамики) в виде

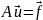, (21.2)

где A - дифференциальный оператор, заданный с надлежащими граничными условиями. Разность 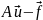равна нулю, а потому равны нулю её проекции на базис , коэффициенты Фурье :

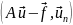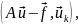k = 1, 2, …, ∞ (21.3)

В большинстве случаев замкнутые аналитические решения задач типа (21.2) недоступны. Но существуют методы, позволяющие получать приближенные решения, которые могут быть как угодно близки к рядам Фурье настоящих решений. Такие методы называются проекционными.

Проекционный метод Галёркина состоит в том, что строится представление решения в виде суммы

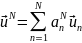(21.4)

с неопределёнными коэффициентами 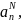и вместо (21.3) берутся N аналогичных соотношений ортогональности

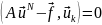; k = 1, 2, …, N. (21.5)

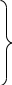( разумеется, должно быть 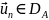, п.19.1). Легко видеть, что эти соотношения порождают систему линейных уравнений

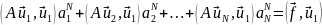
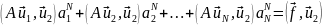
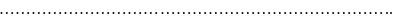
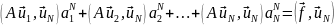
относительно коэффициентов а_п как неизвестных, т. е. в матричной форме:

Ma^N=f, (21.6а)

где в левой части фигурирует вектор, образованный этими коэффициентами 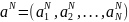и матрица М с элементами 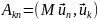,а в правой части - заданный вектор 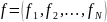с компонентами 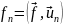(ср. п. 20.1: векторы a^N и f - это то же, что х и b в п. 20.1). Таким образом, метод Галёркина сводит граничную задачу (21.2) к системе линейных уравнений (21.6), решение которой определяет коэффициенты представления (21.4).

Возьмём теперь задачу на собственные значения вида

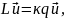(21.7)

где L - некоторый дифференциальный оператор, а q - функция координат. Подобно (21.3) имеем:

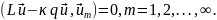(21.8)

Построив представление решения вида (21.4), подчиним его N условиям ортогональности:

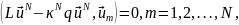(21.9)

подобно тому, как это делалось выше; индекс N при κ подчёркивает, что имеются в виду приближённые собственные значения. Из (21.9) следует однородная система линейных уравнений

Ma^N = κ^NQa^N, (21.10)

где матрицы М и Q имеют элементы M_kn = (Lu_n, u_k) и 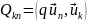соответственно.

Таким образом, первые N собственных значений задачи (21.7) приближённо определяются как корни 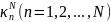характеристического уравнения

Det|M - κ^NQ| = 0 (21.11)

(п. 20.3). Если, в частности q=1, то (21.11) имеет вид

Det|M - κ^NI| = 0, (21.11a)

что совпадает с (20.20). Приближёнными собственными значениями задачи (21.7) являются при этом собственные значения матрицы М.

Для широкого класса задач доказывается сходимость метода Галёркина, т. е. устанавливается тот факт, что

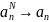при 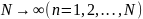, (21.12)

где а_п - коэффициенты Фурье решения .

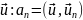21.2. Вариационные принципы и метод Ритца. Рассматривая задачу на собственные значения (21.7), будем считать, что оператор L симметрический, функция q вещественна, а собственные значения κ_n образуют последовательность вида (19.9).

Пусть - произвольная функция 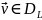. Запишем выражение

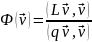(21.13)

Легко видеть, что если 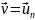- одна из собственных функций, то 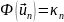есть соответствующее собственное значение.

Выражение (21.13), в котором 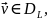может изменяться в некотором классе функций, относится к так называемым функционалам (функционал - «функция от функции»). Можно показать, что функционал 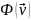имеет минимум, который равен низшему собственному значению v₁:

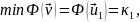(21.14)

а каждое высшее собственное значение есть также минимум Ф(u), но при некотором дополнительном условии, а именно

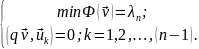(21.15)

Говорят, что функционал (21.13) выражает вариационный принцип для задачи (21.7); вычисление собственных значений 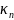можно свести к вариационной задаче нахождения 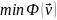(21.15) при переборе всевозможных 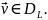Как частную форму функционала (21.13) следует рассматривать выражение (19.6), (19.7) и (19.8). Существуют также вариационные принципы совершенно иного рода, не имеющие связи с задачами на собственные значения. К ним, например, относится принцип Ферма [1].

Ограничивая класс функций, будем искать вместо величину , где 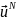есть представление (21.4) решения задачи (21.7); при этом варьируются коэффициенты 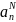. Внося (21.4) в (21.13), имеем:

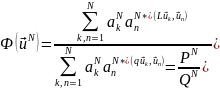(21.15)

Это функция переменных 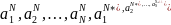(комплексно сопряженные коэффициенты - независимые переменные), и чтобы определить минимум данной функции, надо составить и обратить в нуль производные по всем переменным: условие необходимое, хотя и, вообще говоря, недостаточное. Величину примем за выражение приближённых собственных значений κ^N. Составляя равенства

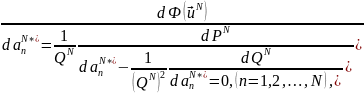
получаем:

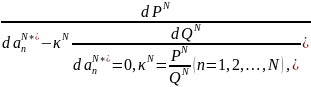(21.17)

т.е

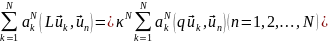
или в матричной форме с использованием обозначений из п. 1:

Ma^N = κ^NQa^N, (21.18)

что совпадает с результатом (21.10), полученным методом Галёркина. Способ, которым было найдено матричное уравнение (21.18), также относится к проекционным методам и называется методом Ритца.

Для задачи (21.2), если оператор А симметрический, тоже можно сформулировать вариационный принцип в виде функционала

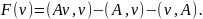(21.19)

Применяя метод Ритца, в данном случае придём к матричному уравнению (21.6а).

Уравнения (21.10), (21.6 а) и аналогичные алгебраические формы, к которым сводится граничная задача путём применения проекционных методов, называются уравнениями Галёркина-Ритца.