14. Вращение декартовой системы координат

14.1. Направляющие косинусы. Поскольку в дальнейшем придется рассматривать поля и волны, различным образом ориентированные в декартовых системах координат, остановимся на преобразованиях, связанных с поворотами системы.

Пусть имеются две системы координат (х, у, z) и (х', у', z') с общим началом 0. Направление каждой из осей второй системы можно охарактеризовать тремя углами с тремя осями первой системы. Таким образом, имеется девять углов

α₁ α₂ α₃

β₁ β₂ β₃

γ₁ γ₂ γ₃

Подобно тому, как углы первой строчки указывают ориентацию оси х' в системе (х, у, z), во второй и третьей строчках характеризуются оси у' и z'. По столбцам же углы указывают ориентацию осей х, y и z в системе (х', у', z').

Единичные координатные векторы (орты) обеих систем обозначим 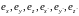соответственно. Очевидно, проекции каждого орта одной системы в другой системе будут равны косинусам введённых углов; они называются направляющими косинусами. Поэтому имеем следующие соотношения:

,

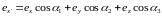
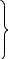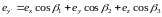, (14.la)

,

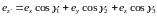
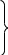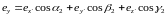, . (14.1б)

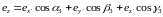
Умножая равенства (14.1а) поочерёдно на , а (14.16) - на 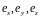, получаем соотношения между направляющими косинусами:

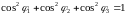
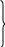φ = α, β, γ

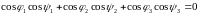ψ = α, β, γ (14.2)

ψ ≠ φ

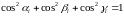i = 1, 2, 3

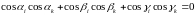k = 1, 2, 3 (14.3)

i ≠ k

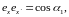
При выводе (14.2) принимается во внимание, что 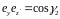и т.д..

Очевидно, что каждую из систем (х, у, z) и (х', у', z') можно рассматривать как результат вращения другой относительно общего начала 0.

14.2. Преобразование компонент векторов и координат. Возьмем некоторый вектор ; мы можем считать его отложенным из начала координат 0. Записывая в каждой из декартовых систем, составляем равенство:

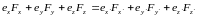
Если произвести здесь умножение на орты обеих систем, то получатся формулы, связывающие проекции вектора в каждой из систем:

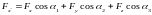
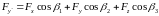_, (14.3a)

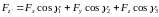
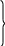
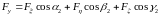. (14.3б)

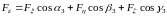
Можно сказать, что при вращении декартовой системы координат происходит преобразование компонент вектора в соответствии с равенствами (14.3). Это однородное линейное преобразование типа (1.11), причём матрица преобразования (1.12) составляется из направляющих косинусов.

Взяв в качестве 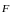радиус-вектор 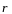_{, равный}

,

вместо (14.3) получим:

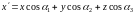
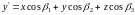_, (14.4a)

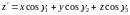
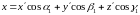
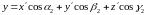. (14.4б)

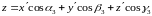
Это правило преобразования координат, как видно, совпадает с правилом преобразования компонент вектора.

14.3. Углы Эйлера. Наконец, надо иметь в виду, что девять углов между осями двух систем координат связаны шестью соотношениями (14.1а,б), поэтому ориентация одной системы координат относительно другой («повёрнутой» относительно «неподвижной») вполне определяется всего тремя углами. Ими могут быть так называемые углы Эйлера Θ, Ф и Ψ, определяемые следующим образом. Плоскости хОу и х'Оу' пересекаются по некоторой прямой, проходящей через начало координат. Угол Θ есть угол между указанными плоскостями (или, что то же самое, между осями z и z'), а Ф и Ψ - углы между упомянутой линией пересечения плоскостей и осями х и х' соответственно.

С помощью трёх последовательных простых вращений можно совместить системы (х, у, z) и (х', у', z'). Выполнив их, мы получим формулы преобразования орто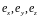в в 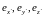через углы Эйлера.

Сначала повернем систему (х, у, z) вокруг оси z на угол Ф (до совмещения осей х и х'). При этом тройка ортов , перейдет в новую тройку 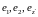, причём на, основании (14.1а)

,

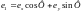
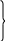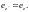
Далее, произведём вращение на угол Θ вокруг линии пересечения плоскостей β до совмещения осей z и z'. При этом тройка ортов переходит в 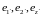. Согласно (14.1а),

_.

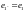
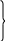
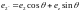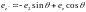
Н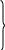 аконец, в результате вращения на угол ψ вокруг оси z тройка переходит в :

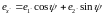
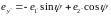
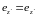
Исключение из девяти записанных уравнений промежуточных ортов 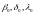даёт:

,

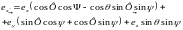
, (14.5)

.

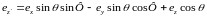Сравнение этого результата с (14.1а) немедленно приводит к выражениям направляющих косинусов (девяти величин) через три угла Эйлера, например:

cosα₁ = cosФ cosψ - cosθ sinФ sinψ,

cosγ₂ = - sinθ cosФ

и т. д.